例 1. [省选联考 2022] 卡牌
考场上压根没往根号分治上想……还是见的题太少了。
首先进行题意转化:对于每个数字 \(i\) 有覆盖的质数集合 \(\text{fac}_i\),对于一次询问质数集合 \(\text{state}\),求有多少种方法选出若干个 \(\text{fac}_i\),使其并集为 \(\rm state\) 的超集。
这看上去就很容斥,可以想到这个很经典的柿子
于是设 \(A_i\) 为包含质数 \(i\) 的方案数,枚举 \(s\) 表示不包含质数集合 \(s\) 的方案数就可以容斥了。问题是质数个数高达 \(300\),直接容斥显然是不行的。真的需要记录下包含所有质数的状态吗?事实上,由于 \(s_i\le 2000\),所以一个数字不可能包含大于等于 \(43\) 的两个质数(\(43\times 47>2000\)),也就是说,对于大于等于 \(43\) 的两个质数 \(x,y\),将分别包含 \(x,y\) 的数字个数进行两两匹配是不会算重的。所以我们可以只记录前 \(13\) 个质数:记 \(f_{s,i}\) 为前 \(13\) 个质数的集合为 \(s\)(表示不包含),包含第 \(i\) 个质数(大于等于 \(43\) 的质数)的选数方案数,对于每个询问就可以直接容斥即可。
例 2. \(\text{[NOI 2015] }\)寿司晚宴
一些闲话:我竟然在 \(2019\) 年做过这题,完全没有印象啊……
还是翻译一下题意:对于每个数字 \(i\) 有覆盖的质数集合 \(\text{fac}_i\),选择若干个质数集合分成两个部分,要求这两个部分之间没有交。还是考虑根号分治,对于大于等于 \(22\) 的质数可以分开考虑。将每个数字按 "大质数"(指大于等于 \(22\) 的质数)排序,对于一段相同 "大质数" 的数字,可以定义 \(f_{0/1,s,t}\) 表示 "大质数" 在 \(0/1\) 边,\(0\) 边质数集合为 \(s\),\(1\) 边质数集合为 \(t\) 的方案数,最后 \(dp_{s,t}\leftarrow f_{0,s,t}+f_{1,s,t}-dp'_{s,t}\),后面减去是减去不选这种 "大质数" 的情况。
例 3. \(\text{HDU - 6315 Naive Operations}\)
一些闲话:\(\rm cnm\),我势能分析是坨 \(\rm shit\)!
对每个区间维护 \(\text{sum}\) 和 \(\min\),其中 \(\min\) 初值为 \(b_i\),每次区间加就将对应区间的 \(b\) 减一。等到减到零时,就遍历到叶子节点暴力修改。复杂度可以这样计算:一共可以全局加 \(n\) 次,那么遍历到叶子节点的次数为 \(n/1+n/2+\dots +n/n\approx n\log n\),所以总复杂度为 \(\mathcal O(n\log^2 n)\).
例 4. \(\text{CF1065D Three Pieces}\)
将每个位置拆成三种棋子,然后可以最短路。关于最短时间基础上的交换次数最小值,可以将 \(\mathtt{dp}\) 值改写成 \(a\cdot M+b\) 的形式(\(b\) 远小于 \(M\))。
例 5. \(\text{LCM from 1 to n}\)
题目大意:给定 \(n\),求 \(1\) 到 \(n\) 的所有数的最小公倍数,对 \(2^{32}\) 取模。多组询问,\(n\le 10^8\).
记 \(L(x)\) 为 \(1,2,\dots,x\) 的 \(\rm lcm\),那么有
可以写一个筛法,用压位来优化 bool 数组的存储,在对每个质数预处理在它之前的质数积 \(f(p)\).
计算 \(L(n)\) 时将 \(n\) 质因数分解,找到 \(n\) 最大质因子 \(p'\),将答案赋初值为 \(f(p')\),再根据公式乘上若干个质数即可。
例 6. \(\rm Freda\) 的迷宫
题意简述:给定一张连通无向图,有 \(q\) 个询问,每次询问 \(x,y\) 之间是否有且只有一条简单路径。
\(x,y\) 之间有且只有一条简单路径等价于 \(x,y\) 之间存在一条路径,使得路径上所有边均为桥(事实上这样的路径只存在一条)。用并查集连接桥的两个端点,那么询问只用判断 \(x,y\) 在并查集中是否连通即可。
例 7. \(\text{[AHOI 2007] }\)密码箱
一些闲话:想在考试前做点水题,结果不会做……这几天状态不佳。
首先转化题意,就是求 \(x^2\equiv 1\pmod n\) 的 \(x\) 个数。整除是比较好判断的,所以转化成 \(n\mid (x-1)(x+1)\),由于没有限制上界,所以不能直接枚举。
考虑这其实等价于能划分出 \(n=ab\),满足 \(a\mid (x-1)\),\(b\mid (x+1)\),所以枚举 \(a\le b\),再枚举倍数即可。
例 8. \(\text{[AHOI 2022] }\)钥匙
一些闲话:今天上午调 "排列" 这道题调自闭了,又犯了很多神必错误,缝缝补补开了 \(+\infty\) 个没有用的数组……但是好像还蛮快?交过了才发现复杂度是 \(\mathcal O(n\log n)\) 的,之前一直以为是 \(\mathcal O(n\sqrt n)\) 的 /kk.
首先,将颜色分开考虑,这个可以用虚树实现。考虑一条链上钥匙与宝箱的匹配,可以将其想象为括号匹配的过程,容易发现这样贪心地匹配一定是最优的。现在考虑同一种颜色钥匙只有 \(5\) 把的条件,直接以每把钥匙 \(x\) 为根进行 \(\rm dfs\) 括号匹配找到可行的宝箱 \(y\),那么一个点在 \(x\rightarrow y\) 路径 \(x\) 侧、另一个点在 \(y\) 侧的询问金币数就可以加一。把树转到 \(\rm dfs\) 序上,可以发现这就是一个矩形加,单点查询的问题,可以扫描线求解,核心代码放在下面了:
bool isanc(int x,int y) {
return dfn[y]>dfn[x] && dfn[y]<=dfn[x]+sz[x]-1;
} /* check if x is the ancestor of y */
int Son(int x,int y,int ret=0) {
while(tp[x]^tp[y]) ret=tp[x], x=f[tp[x]];
if(x==y) return ret; return Ref[dfn[y]+1];
} /* find the son of y which is on the path */
void doIt(int a,int b,int c,int d) {
if(a>b || c>d) return;
modi[a].emplace_back(make_pair(c,1)),
modi[a].emplace_back(make_pair(d+1,-1)),
modi[b+1].emplace_back(make_pair(c,-1)),
modi[b+1].emplace_back(make_pair(d+1,1));
} /* [a,b] & [c,d] */
void insert(int x,int y) {
if(isanc(x,y)) {
int sn = Son(y,x);
doIt(1,dfn[sn]-1,dfn[y],dfn[y]+sz[y]-1);
doIt(dfn[sn]+sz[sn],n,dfn[y],dfn[y]+sz[y]-1);
} else if(isanc(y,x)) {
int sn = Son(x,y);
doIt(dfn[x],dfn[x]+sz[x]-1,1,dfn[sn]-1);
doIt(dfn[x],dfn[x]+sz[x]-1,dfn[sn]+sz[sn],n);
}
else doIt(dfn[x],dfn[x]+sz[x]-1,dfn[y],dfn[y]+sz[y]-1);
}
例 9. \(\text{CF1666I Interactive Treasure Hunt}\)
设两个坐标分别为 \((x_1,y_1),(x_2,y_2)\),同时我们发现 \((x_1,y_2),(x_2,y_1)\) 在 \(\rm scan\) 操作中是完全等价的,所以在求出合法 \(x_1,y_1,x_2,y_2\) 后,还需要用 \(\rm dig\) 进行一次判断,加上输出答案的次数总共三次。
还剩四个询问,就是解方程嘛,但是设出的方程最好能够去掉恼人的绝对值,所以不妨先询问 \((1,1),(n,1)\),这样就可以得到 \(x_1+y_1,x_2+y_2\) 的结果。自然而然地,我们想构造出 \(x_1,x_2\)、\(y_1,y_2\) 异号的方程,问题是我们并不知晓在 \(x_1,x_2\) 中间的数值……吗?直接用 \((x_1+x_2)/2\) 不就好了吗?查询 \(((x_1+x_2)/2,(y_1+y_2)/2)\),我们就得到了 \(x,y\) 坐标之差的和。于是再构造一个 \(((x_1+x_2)/2,1)\) 就是 \(x\) 坐标之差加上 \(y_1+y_2\),用上面的柿子解出 \(x\) 坐标之差,其它就都可以解了。
好水啊。
例 10. \(\text{pkusc 2022}\) 撸猫
题意简述:作为一个喜欢猫的女孩子,糖糖家里养了 \(n\) 只猫。这些猫从 \(1\) 到 \(n\) 标号。
她每天最喜欢的事情就是撸猫,可惜猫猫并不是每天都愿意被她撸。愿意被她撸的猫猫集合 \(S \subseteq [n]\) 根据某个概率分布 \(P\) 随机而来。
在知道了哪些猫猫愿意被撸之后,糖糖可以选择某一只愿意的来 \(\rm rua\)。注意,如果 \(S\) 集合为空,则糖糖不能撸任何一只猫。同时,糖糖的撸猫策略可以带有随机性。比如,在知道了 \(1,2\) 号猫猫都愿意被撸之后,她可以以 \(50\%\) 的概率撸第一只猫,以另外 \(50\%\) 的概率撸第二只猫。
作为一个公平的女孩子,糖糖希望给每一只猫猫更多被 \(\rm rua\) 的机会。她希望设计一个撸猫的策略来最大化 \(\operatorname{Pr}[i_{\text{被撸}} | i\in S]\) 的最小值。换句话说,令 \(p_i = \operatorname{Pr}[i\in S]\) 是第 \(i\) 只猫猫愿意被撸的概率。我们需要设计一个撸猫的策略来最大化常数 \(c\),使得每只猫被撸的概率至少是 \(c\cdot p_i\).
\(n\le 20\).
首先应该想到二分答案 \(c\),那么问题转化成二分图上的网络流问题:右部是 \(2^n\) 个点表示每种愿意被撸的猫猫集合,出边容量为这种情况的概率,左部是 \(n\) 只猫,入边容量为 \(c\cdot p_i\),答案合法当且仅当左部满流。
直接实数网络流是不可行的,事实上可以用 \(\rm hall\) 定理来优化复杂度!乍一看非常离谱,因为用 \(\rm hall\) 定理判断二分图左部满流实际上是 \(\mathcal O(2^n)\) 的,但由于原图的特殊性 —— 右部点数达到了 \(2^n\),所以用 \(\rm hall\) 定理判断反而更优 😶🌫️。
具体再讲一下如何判定:将入/出边的容量进行拆点(?,那么实际上是判断左部形成的任意集合 \(S\) 所包含的入边容量和 \(g(S)\) 与所有包含 \(S\) 中任意猫的右部点的出边容量之和的大小关系。
\(g(S)\) 可以每次二分 \(\mathcal O(2^n)\) 地计算,后面那一坨实际上就是用总概率减去 \(U\setminus S\) 的所有子集的概率,高维前缀和预处理即可。
例 11. 点权和
题意简述:给你一棵树,最开始点权为零,每次将与一个点 \(x\) 树上距离 \(\leqslant 1\) 的所有点点权加一,之后询问这些点修改后的点权和。复杂度需线性。
分别维护自己、所有儿子、所有孙子被修改了几次即可。
例 12. \(\text{[LNOI 2022] }\)吃
一些闲话:\(\rm LNOI\) 的两道 "提高+" 我都不会做,今日之难绷 😅。
首先将 \(a_i=1\) 的食物按加 \(b_i\) 来吃,并记得到的和为 \(s\),\(w=\prod a_i\)。然后有一个结论:一定存在一种最优方案满足只选一个来加或者一个都不加。证明不妨设 \(b_i\leqslant b_j\),那么两个都选的体重即为 \((s+b_i+b_j)\cdot (w/a_i/a_j)\),而只选 \(b_j\) 的体重为 \((s+b_j)\cdot (w/a_j)\),显然 \(s\cdot (w/a_j)>s\cdot (w/a_i/a_j)\),接下来只用证
可以发现
结论得证。一个都不加的证法同理,这里不再赘述。
例 13. \(\text{[NOI 2021] }\)量子通信
一些闲话:去年的时候根本不能理解这题的分块欸 /kk,话说某谷的评测姬真的好慢啊。
将每个串分成 \(16\) 块,由于 \(k\leqslant 15\) 以及鸽笼原理,所以如果一个串没有受到 \(\rm Eve\) 的干扰,至少会存在一个块与字典中的某个串的对应块匹配。考虑能与某个块匹配的串的期望个数,实际上是 \(\dfrac{2^{256-16}}{2^{256}}\cdot n\approx 6\),所以暴力遍历复杂度是可接受的。
例 14. \(\text{[NOI 2021] }\)庆典
遇到可达性问题先进行缩点。接着考虑题目条件会赋予图怎样的性质 —— 事实上,缩点后的图一定是下图这样类树的形态:
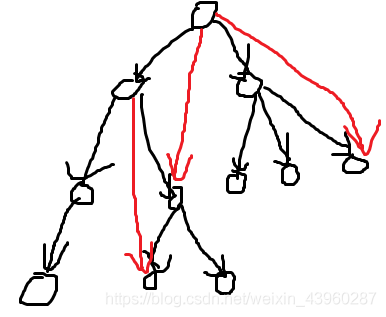
且原图只有一个根节点,因为题目保证将边改为无向边后原图连通,那么如果存在两个入度为零的点 \(x,y\),一定有 \(x\Rightarrow z,y\Rightarrow z\) 成立,于是一定满足 \(x\Rightarrow y\) 或 \(y\Rightarrow x\),与假设矛盾。除此之外,红色边都是没用的,这个可以用拓扑排序去除,即选择最后一个到达 \(v\) 的 \(u\) 作为 \(v\) 在树上的父亲。
由于每次新加的边很少,我们可以直接用虚树解决此问题。预处理每个点到根的权值和[1],建树时将边权设为两点在原树上的权值距离[2],最后从 \(s\) 所在强连通分量开始 \(\rm dfs\),并给路过的点打标记,再从 \(t\) 所在强连通分量遍历,遇到标记点与标记点之间的边就累积贡献。复杂度大概是 \(\mathcal O(n\log n)\) 再带一个比较小的系数。
震惊!这题我开了五个 \(\rm vector\) 都能轻松跑过 😭!
例 15. \(\text{CF915D Almost Acyclic Graph}\)
判环想到拓扑排序,可以发现,删掉边 \((u,v)\) 在拓扑排序中表现为 \(v\) 的入度减一。事实上,我们不用枚举边,直接将每个点的入度减一,再进行拓扑排序即可。可以感受到我们将拓扑排序变成了一个像网络流一样动态的操作,每次选择最能拖延 \(v\) 入队的边进行删除。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号