\(\text{I love Wordle!!!}\)
I guessed this 5-letter word in 6/6 tries.
⬛⬛🟨⬛⬛
⬛⬛⬛⬛🟨
🟨🟨🟨⬛⬛
🟨🟨⬛🟨⬛
⬛🟩🟩🟩🟩
🟩🟩🟩🟩🟩
Can you guess this word?
\(\frak{Description}\)
\(\frak{Solution}\)
一点题外话:"高端的食材,往往只需要简单的烹饪。"
回归正题,先处理出所有能被覆盖的景点数,即为第一问的答案。剩下的部分需要知道一个结论:
对于一个合法(即覆盖所有点,且所有圆都与太阳花田有交)的圆与点的匹配,一定为每个圆匹配的点是按照 \(x\) 排序后的一段。
证明可以看看下面这张图:
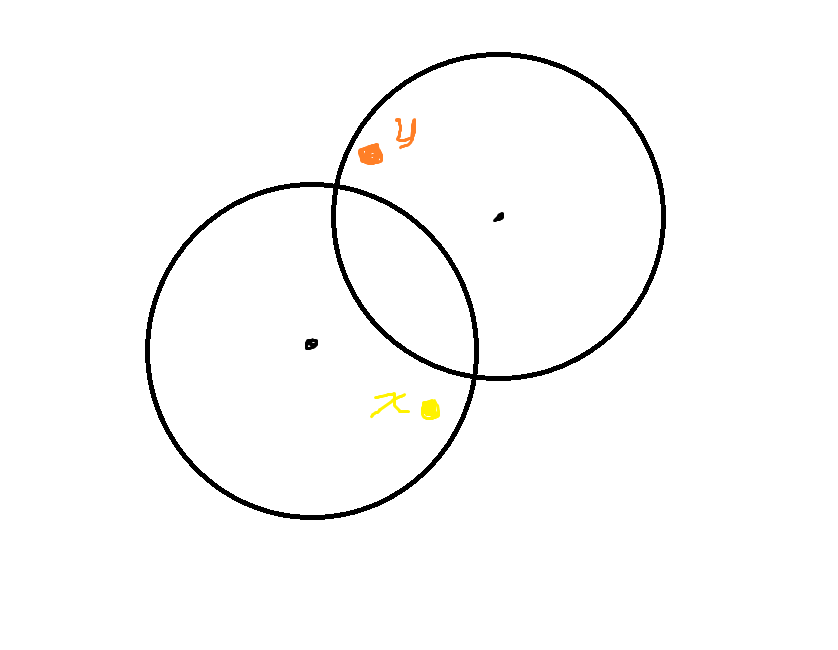
不妨令太阳花田的边界恒为水平,我们可以适当旋转这张图使得 \(x\) 的横坐标大于 \(y\) 的横坐标,若前一个圆能取到点 \(x\) 但取不到点 \(y\),后一个圆能取到点 \(y\) 但取不到点 \(x\) 的情况不可能存在即可证明此命题。其实 "圆心必在太阳花田外,点必在太阳花田内" 是一个很强的限制,它强制了 \(x,y\) 必须至少相对 两圆心连线 在同侧,转一转就能发现这种情况一定不存在。
现在我们证明了每个圆统治了 完整 的一段点区间,那当然每个圆匹配(可以匹配 \(\ne\) 匹配)的点就是按照 \(x\) 排序后的一段咯。
那这个结论能否拓展到圆半径不同的情况呢?可惜这是行不通的。我这里嫖了一张图:
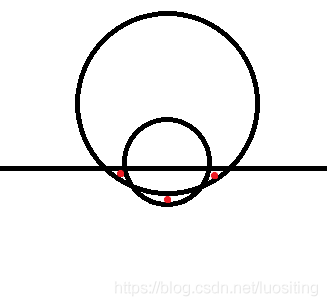
我猜想,这个结论对于 "两圆的交由两个圆的劣弧组成" 的情况是成立的,但如果存在优弧,就会出现上图的情况。
不过这个结论有啥用呢?先给出异常朴素的 \(\mathtt{dp}\) 定义:令 \(dp_{i,j,k}\) 为前 \(i\) 个景点,上一个使用的圆(\(y>R\))为 \(j\),上一个使用的圆(\(y<0\))为 \(k\) 的最小花费,在 \(\mathtt{dp}\) 之前,还需要将所有景点按横坐标排序。你可能感觉这个 \(\mathtt{dp}\) 状态有什么大病,因为如果不记录选过的圆,可能出现选 \(x\) 后选 \(y\),然后又选 \(x\),这不就重复统计 \(x\) 的花费了吗?依据结论,这种情况实际上并不存在。时间复杂度是朴实无华的 \(\mathcal O(n^4)\).
彩蛋:学习隔壁老王的博客得到一个网络流的 \(\rm trick\),就是对于 "优先选择哪些边" 时,可以用费用流,将优先边赋一个更优秀的权值。
\(\frak{Code}\)
#include <cstdio>
#define print(x,y) write(x),putchar(y)
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while((s=getchar())>'9' || s<'0')
f |= (s=='-');
while(s>='0' && s<='9')
x = (x<<1)+(x<<3)+(s^48),
s = getchar();
return f?-x:x;
}
template <class T>
inline void write(T x) {
static int writ[50], w_tp=0;
if(x<0) putchar('-'),x=-x;
do writ[++w_tp]=x-x/10*10,x/=10; while(x);
while(putchar(writ[w_tp--]^48),w_tp);
}
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 105;
ll R;
int dp[maxn][maxn][maxn];
int n,m,co[2][maxn],p1,p2,c[maxn];
struct node {
int x,y;
bool operator < (const node& t) const {
return x<t.x;
}
} s[maxn],t[maxn],p[2][maxn];
bool arr(const node& i,int j) {
return 1ll*(i.x-s[j].x)*(i.x-s[j].x)+
1ll*(i.y-s[j].y)*(i.y-s[j].y)<=R;
}
int main() {
n=read(9), m=read(9), R=read(9); R*=R;
for(int i=1;i<=n;++i) s[i].x=read(9), s[i].y=read(9);
for(int i=1;i<=m;++i) t[i].x=read(9), t[i].y=read(9), c[i]=read(9);
int siz=n; n=0;
for(int i=1;i<=siz;++i) for(int j=1;j<=m;++j)
if(arr(t[j],i)) { s[++n] = s[i]; break; }
sort(s+1,s+n+1);
print(n,'\n');
for(int i=1;i<=m;++i)
if(t[i].y<0) p[1][++p2]=t[i], co[1][p2]=c[i];
else p[0][++p1]=t[i], co[0][p1]=c[i];
memset(dp,0x3f,sizeof dp); dp[0][0][0]=0;
for(int i=1;i<=n;++i)
for(int j=0;j<=p1;++j) for(int k=0;k<=p2;++k) {
if(j && arr(p[0][j],i)) {
dp[i][j][k] = min(dp[i][j][k],dp[i-1][j][k]);
for(int l=0;l<=p1;++l)
dp[i][j][k] = min(dp[i][j][k],dp[i-1][l][k]+co[0][j]);
}
if(k && arr(p[1][k],i)) {
dp[i][j][k] = min(dp[i][j][k],dp[i-1][j][k]);
for(int l=0;l<=p2;++l)
dp[i][j][k] = min(dp[i][j][k],dp[i-1][j][l]+co[1][k]);
}
}
int ans = 0x3f3f3f3f;
for(int i=0;i<=p1;++i)
for(int j=0;j<=p2;++j)
ans = min(ans,dp[n][i][j]);
print(ans,'\n');
return 0;
}
