常见结论
结论 1:当 \(n\ \&\ m=m\) 时,\(\text C(n,m)\) 是奇数。
证明戳这。
结论 2:\(\sum_{i=0}^n \text{C}^2(n,i)=\text{C}(2n,n)\)。
两个盒子各有 \(n\) 个球,共取 \(n\) 个球的方案数是 \(\text{C}(2n,n)\),这也相当于一个盒子取 \(i\) 个,另一个取 \(n-i\) 个。所以实际上这可以拓展到两个盒子有 \(n,m\) 个球的情况。
结论 3:\(\text{C}(n,m)=\text{C}(n-1,m-1)+\text{C}(n-1,m)\)。
第 \(n\) 个元素取或不取。
结论 4:\(\sum_{i=0/j}^{n}\text C(i,j)=\text C(n+1,j+1)\)。
证明用归纳法,可以证明 \(n=0\) 的情况成立。然后有:
结论 5:\(\sum_{i=0}^n i^2\text{C}(n,i)=2^{n-2}n(n+1)\)。
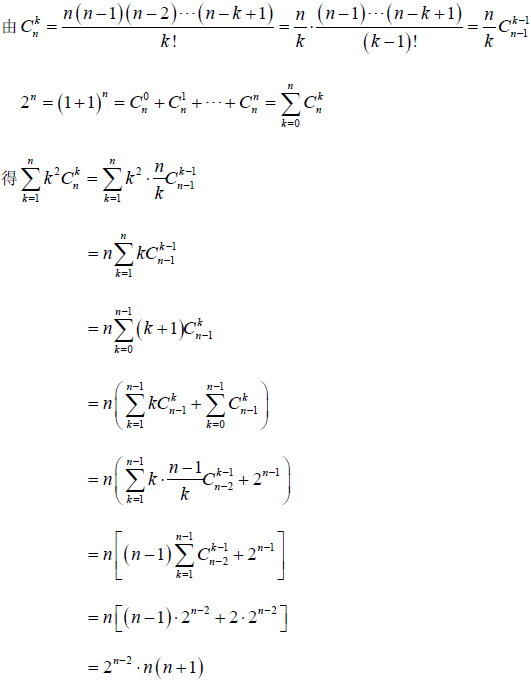
结论 6:
\[D(n)=n!\sum_{i=0}^n\frac{(-1)^i}{i!} \]\[=n\cdot D(n-1)+(-1)^n \]
这个可以用二项式反演证!令 \(f(i)\) 为长度为 \(i\) 的排列数。那么有:
后面的递推式可以通过这个式子化出来。
结论 7:
\[\sum_{n+m=N}\binom{n}{s}\cdot \binom{m}{t}=\binom{N+1}{s+t+1} \]
在 \(N+1\) 个球中取出 \(s+t+1\) 个球。相当于枚举第 \(s+1\) 个球的位置。
结论 8:
\[\large \sum_{k=0}^m \begin{pmatrix} m\\k \end{pmatrix} \begin{pmatrix} n\\k \end{pmatrix}=\begin{pmatrix} m+n\\m \end{pmatrix} \]
结论 9:
\[\binom{n+r+1}{n}=\sum_{i=0}^n \binom{i+r}{i} \]
其实和 结论 4. 有一个同一个名字 —— 上指标求和。
对于此结论,你可以用 结论 3. 对上指标较小的组合数进行拆分(这里的上指标指的反而是下面的部分)。
而对于 结论 4.,你需要的是对上指标较大的组合数进行拆分!
结论 10:
\[\binom{n}{k}=(-1)^k\cdot \binom{k-n-1}{k} \]
上指标反转求和。
结论 11:
\[\sum_{i=0}^k(-1)^i\cdot \binom{n}{i}=(-1)^k\cdot \binom{n-1}{k} \]
结论 12:从 \(n\) 种不同的小球中选择 \(m\) 个,每种小球的数量为无限个,则方案数为 \(\binom{n+m-1}{m}\).
首先可以明确,一种合法方案一定是选择 \(i\) 种小球,再枚举每种小球的重复次数(这就是隔板法),这可以用一个柿子表示:
例题
例 1. 将长度为 \(n\) 的序列分成 \(m\) 段的方案数,允许段为空。或者,你会发现这和将 \(n\) 个相同的球放进 \(m\) 个不同的抽屉是等价的。
终于找到一个能说服我的 理解 了!
现在突然有了一种船新的理解!在 \(n+m-1\) 中选择 \(m-1\) 个分隔符,显然分出的序列可以为空。
例 2. \(\text{HDU - 5794 A Simple Chess}\)
可达点满足 \((x+y)\bmod 3=2\) 可以归纳证明。每次 \(x,y\) 坐标和都会增加 \(3\)。
例 3. \(\text{arc110D - Binomial Coefficient is Fun}\)
如果确定了 \(b\),答案就是非常好求的。所以一种思路就是先用组合数算 \(b\),再来算答案。在 \(n+m\) 中选择 \(n\) 个分隔符,将整个序列分成 \(n+1\) 段。显然我们不要求分成的段有顺序,于是不妨令前 \(i,i\in[1,n]\) 段对应 \(a_i\) 选择的 \(b_i\)。最后一段相当于满足 \(\sum b_i\le m\) 的限制。答案就是 \(\text{C}(n+m,n+\sum a_i)\)。只要选出 \(n+\sum a_i\) 个数,因为 \(a_i\) 是固定的,方案也就固定了。
\(\text{Upd:}\) 可以利用 结论 7。推广一下可以得到 \(n\) 个组合数相乘的式子:\(\binom{\sum b_i+n-1}{\sum a_i+n-1}\)。接下来只用算 \(\sum_{\sum b_i\le m} \binom{\sum b_i+n-1}{\sum a_i+n-1}\)。利用 结论 4 可知答案为 \(\binom{m+n}{\sum a_i+n}\)。
例 4. \(\text{abc171F - Strivore}\)
如果随便填会有重复的情况。考虑枚举原串的第一个字符的位置 \(i\),规定如果有相同字符,选择最后面的字符为原串字符。前 \(i-1\) 个位置为 \(26^{i-1}\),后面取 \(k+m-i\) 个位置放 \(m-1\) 个字符,为 \(\binom{k+m-i}{m-1}\)。剩余位置不能和左边最近的原串字符相同,但如果中间隔了另一个不同的原串字符就不影响,为 \(25^{k-i+1}\)。
例 5. \(\text{[HNOI 2011] }\)卡农
当所选集合有顺序时更方便我们考虑问题(相当于在 \(m\) 个位置放集合),不妨先不管同种音乐的限制,最后将答案除以 \(m!\) 即可。
考虑题目的三个限制:
- 所选集合不为空。
- 两两集合不同。
- 对于 \(i\in [1,n]\),\(i\) 在所选集合中出现次数和为偶数。
对于第一个限制,我们就只能选 \(2^n-1\) 种集合。设 \(dp_i\) 为在前 \(i\) 个位置放集合的合法方案数。有个很神奇的转化 —— 确定前 \(i-1\) 个集合,相当于确定第 \(i\) 个集合中 \(j\in [1,n]\) 出现次数的奇偶性。而 \(i\) 在某个集合只能出现 \(0/1\) 次,所以相当于确定了第 \(i\) 个集合。方案数为 \(\text{A}(2^n-1,i-1)\)。
不过可能出现第 \(i\) 个集合为空集的情况。这种情况的方案数为 \(dp_{i-1}\)。
还要排除第 \(i\) 个集合与前面的某 \(j\) 集合相同的情况。那么所有数在 \(i,j\) 集合的出现次数必定为偶数,所以剩余 \(i-2\) 个集合方案数为 \(dp_{i-2}\)。不过我们需要在前 \(i-1\) 个位置中给 \(j\) 找一个位置,有 \(i-1\) 的系数。\(i,j\) 集合的取值方案就是 \(2^n-1-(i-2)\)。
例 6. 求 \(n\) 个数里面取 \(i\) 个数异或的所有组合的和。\(n \le 1000,\ i\in[1,n]\)。
对每一位进行计算。设某一位有 \(k\) 个 \(0\),对于每个 \(i\),枚举从 \(k\) 个 \(0\) 中选 \(t\) 个数,从 \(n-k\) 个 \(1\) 中选 \(i-t\) 个数。方案数为 \(\binom{k}{t}\cdot \binom{n-k}{i-t}\),这些方案是否有贡献和 \(n-k\) 的奇偶性有关。
例 7. \(\text{agc043B - 123 Triangle}\)
手玩一下发现第二行就没有 \(3\) 了,所以将整体 \(-1\),这不影响相邻两项的差。
还有个性质:如果序列中有 \(1\),答案不可能为 \(2\)。因为 \(1\) 和 \(0,2\) 都会变成 \(1\)。在这种情况下,我们就只用判断答案的奇偶性。
例 8. \(\text{Link with Balls}\)
首先可以发现第一个桶、\(2i,2i+1\) 的合并桶都可以取出任意个球,剩下第 \(2n\) 个桶能取 \([0,n]\) 之间的球。
于是可以枚举最后一个桶取了多少球,剩下球的方案可以用插板法解决。
数据范围太大?用 结论 4.!
例 9. 怎么又双叒叕是括号序列?
题目大意:求有多少个长度为 \(n\) 的括号序列满足其所有子序列中最长合法括号 子序列 的长度恰好为 \(2k\). 多组数据。\(n,T\le 10^5\).
先放一张嫖过来的图:
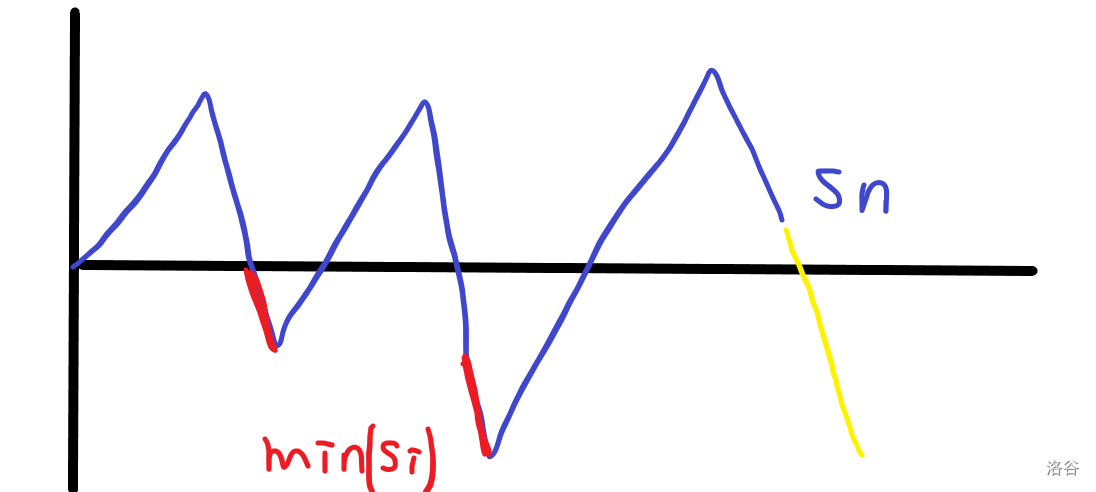
自己做是不可能想到的,只有记住这个结论了罢……
首先一个 \(\rm trick\) 是遇到括号序列就转成 \(+1/-1\),然后 上图理解。
这题有个结论是 "最长合法括号子序列长度为 \(n-s_n+2\cdot \min s_i\)"。首先需要再强调的一点是要求的是子序列,所以可以将多个合法括号子串拼在一起。对于具体证明,就是找出取到 \(\min s_i\) 的位置 \(p\)(多个是不影响的),其实位置 \(p\) 之前的段和之后的是很相似的。
为什么这么说呢?在 \(p\) 之前的段只浪费了红线部分,也即只有多余的右括号会造成浪费;而对于在 \(p\) 之后的段则只会浪费左括号。如果从 \(n\) 一端向 \(p\) 看,和从 \(0\) 向 \(p\) 看其实是一样的!
那么之前段的浪费就是 \(\min s_i\) 与 \(0\) 的距离,而之后段的浪费就是 \(\min s_i\) 与 \(s_n\) 的距离。于是易得浪费的括号个数是 \(|\min s_i|+|s_n-\min s_i|\),用 \(n\) 减去这个值就证明了结论。
由 \(2k=n-s_n+2\cdot \min s_i\),我们现在可以知道 \(s_n\) 与 \(\min s_i\) 之间的等式关系。不妨枚举 \(\min s_i=t\)(实际上二者都可以被枚举),接下来就又到了喜闻乐见的数数环节了!
其实这挺像卡特兰数的几何推导,所以我们也可以利用 "容斥" 与 "翻折" 这两个技巧。
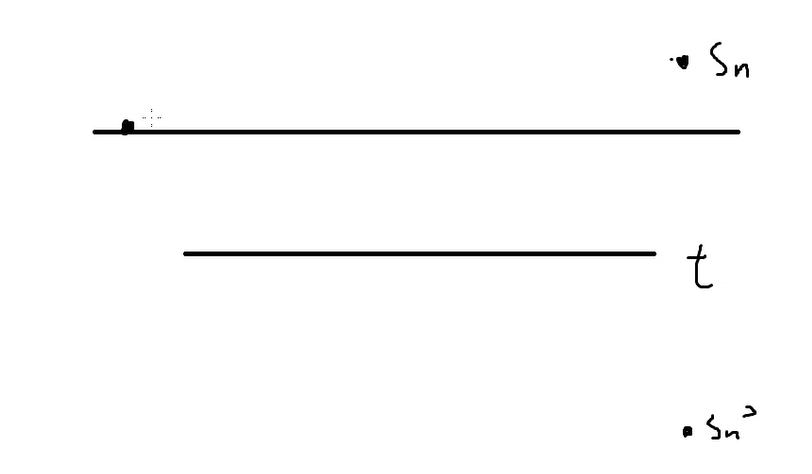
答案是从 \((0,0)\) 走到 \((n,s_n)\) 且 到达但不过 \(y=t\) 这条直线的方案数,就可以转化为 "从 \((0,0)\) 走到 \((n,s_n)\) 不经过 \(y=t-1\) 这条直线的方案数" 减去 "从 \((0,0)\) 走到 \((n,s_n)\) 不经过 \(y=t\) 这条直线的方案数"。
而对于 "不经过直线 \(y=t\)" 可以翻译成 "从 \((0,0)\) 出发到达 \((n,s_n)\) 的方案数" 减去 "从 \((0,0)\) 出发到达 \((n,s_n')\) 的方案数"。其中 \(s_n'\) 是 \(s_n\) 相对 \(y=t\) 的对称点。
对于不经过 \(y=t-1\) 这条直线的方案数,令右括号个数为 \(x\),左括号为 \(y\),可以通过解一个方程组来得到 \(x,y\),这里就不再赘述:
最后得到答案是 \(\binom{n}{k}-\binom{n}{k-1}\),我们神奇地将 \(t\) 消掉啦!
最后还有 \(t\le s_n\) 的限制,可以解出 \(t\) 有 \(n+1-2k\) 种取值,这道题就做完了。

