\(\frak{Description}\)
\(\frak{Solution}\)
首先二分延长时间 \(T\),接下来容易想到用网络流判定是否成立。首先从源点向奶酪连容量为 \(p_i\) 的边,由于每个奶酪有保质期,也就是说我们有 \(2n-1\) 个不同的时间段,需要分时间段建图。接下来就只用考虑 一个时间段内 的情况,并假设这个时间段长度为 \(L\).
那老鼠怎么建边呢?显然我们不能将每个奶酪向老鼠 \(i\) 连容量为 \(v_iL\) 的边,再从老鼠 \(i\) 向汇点连容量为 \(v_iL\) 的边,因为无法保证题目中最重要的条件:
- 每只老鼠在同一时间只能吃一个奶酪;
- 每个奶酪在同一时间只能被一只老鼠吃。
接下来给出正确的建图:将老鼠的速度从大到小排序,令 \(d_i=v_{i-1}-v_i\)(不妨令 \(v_0=0\)),称其为第 \(i\) 只新老鼠的速度。至于是怎么想到的,你可以先简单地做一个 不太正确 的预测:一个奶酪连多只原老鼠 \(\rightarrow\) 同时被多只老鼠吃;一个奶酪连多只新老鼠 \(\rightarrow\) 多个差分值累积成一只老鼠。
为了方便下文部分的理解,这里给出一张图,再深入阐述一下 \(v_i\) 与 \(d_i\) 之间的关系(图是从 \(\rm ikrvxt\) 那嫖的 qwq):
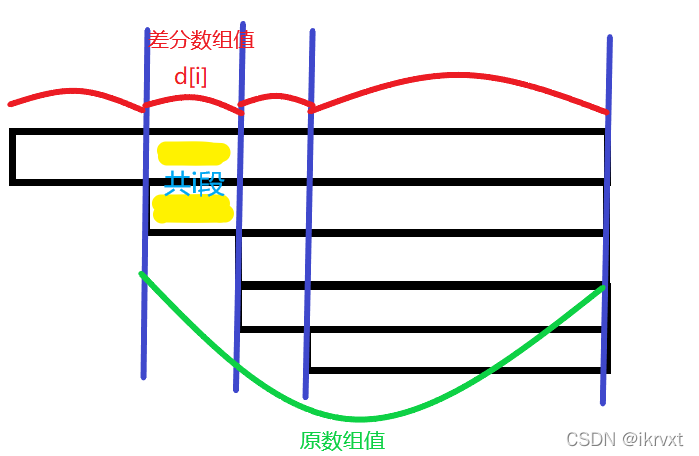
给出一个重要的 \(\rm observation\) 是假设 \(1\) 到 \(i\) 的原老鼠(排完序后)总共吃了 \(t\) 时间,显然它们的速度都包含 \(d_i\),所以相当于 \(i\) 号新老鼠吃了 \(t\) 时间。
建出新老鼠点 \(i\) 后,从每个奶酪向其连容量为 \(d_iL\) 的边,再从新老鼠点向汇点连容量为 \(d_iL\cdot i\) 的边。前者是容易理解的,就把新老鼠看成真正的老鼠就行;对于后者,考虑对于新老鼠 \(i\) 而言,它吃奶酪最多的情况是 "所有 \(1\) 到 \(i\) 的原老鼠都吃满了 \(L\) 时间(注意可以吃不同奶酪)",也就是 \(d_iL\cdot i\). 同时也注意到 \(\sum_{i=1}^m d_iL\cdot i\) 和 \(\sum_{i=1}^m v_iL\) 在数值和意义上都是匹配的。最后跑一遍最大流,查看源点连出的边是否满流即可。
接下来我们证明,这样建图可以使跑出的答案 经过一定的调整 满足上文两个重要的条件。
-
每只老鼠在同一时间只能吃一个奶酪:
假设第 \(j\) 只原老鼠吃第 \(i\) 个奶酪吃了 \(t_i\) 时间。那么若 \(\sum t_i>L\),就说明这只原老鼠在同一时间不止吃了一个奶酪。我们应用一种策略:让速度更快的原老鼠帮助原老鼠 \(j\) 吃来不及吃的奶酪,这相当于提高吃奶酪的效率。另外,由于是帮助吃奶酪,所以不会出现多只原老鼠吃一个奶酪。如果吃完了,说明调整后的 \(t_i'\) 满足 \(\sum t_i'\le L\),满足条件。
反之,就说明所有速度更快的原老鼠(即 \(1\) 到 \(j-1\) 的原老鼠)都已经吃满了 \(L\) 时间。这时我们转回新老鼠点的角度,应用上文的 \(\rm observation\),则点 \(j\) 因为 "速度更快的原老鼠都已经吃满了 \(L\) 时间" 流出了 \(d_jL\cdot (j-1)\) 的流量,同时第 \(j\) 只原老鼠使点 \(j\) 又至少流出 \(d_j\cdot \sum t_i'\) 的流量,总共流出 \(d_jL\cdot j+d_j\cdot \big((\sum t_i')-L\big)>d_jL\cdot j\). 这都比流出的容量大了,所以这种情况是不合法的。
-
每个奶酪在同一时间只能被一只老鼠吃:
类似上文的证明,假设第 \(j\) 个奶酪被第 \(i\) 只原老鼠吃了 \(t_i\) 时间。那么若 \(\sum t_i>L\) 就说明这个奶酪在同一时间被多只原老鼠吃。还是应用上文的 \(\rm observation\),我们考虑最极端的情况,即第 \(m\) 个新老鼠点,那么它应该从奶酪 \(j\) 流入 \(d_m\cdot \sum t_i\) 的流量,但实际上从奶酪 \(j\) 流入点 \(m\) 的容量都只有 \(d_mt_m\)!所以不合法。
最后有一个困扰了博主很久的问题,但是暂时也想不出解决方案,就先放在这里 qwq
对单个奶酪 \(k\) 列式,令 \(t_i\) 为第 \(i\) 只原老鼠吃这个奶酪花费的时间,那么有(令 \(v_{m+1}=0\)):
显然我们跑出 \(\langle k,i \rangle\) 边的流量除以 \(v_i-v_{i-1}\) 就是 \(\sum_{j=1}^i t_j\),反解可以得到 \(t_i\),但是,我们怎么保证 \(t_i\ge 0\)?
\(\frak{Code}\)
#include <cstdio>
#define print(x,y) write(x),putchar(y)
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while((s=getchar())>'9' || s<'0')
f |= (s=='-');
while(s>='0' && s<='9')
x = (x<<1)+(x<<3)+(s^48),
s = getchar();
return f?-x:x;
}
template <class T>
inline void write(T x) {
static int writ[50],w_tp=0;
if(x<0) putchar('-'),x=-x;
do writ[++w_tp]=x-x/10*10,x/=10; while(x);
while(putchar(writ[w_tp--]^48),w_tp);
}
#include <queue>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int SIZE = 2000;
const int infty = 1e9;
const double eps = 1e-7;
queue <int> q;
double all;
int n,m,p[40],r[40],d[40],s[40],S,T;
int head[SIZE],cnt,arc[SIZE],dis[SIZE];
vector <double> v;
struct edge {
int nxt,to;
double w;
} e[(int)3e5];
bool bfs() {
while(!q.empty()) q.pop();
for(int i=1;i<=T;++i)
dis[i]=infty, arc[i]=-1;
q.push(S), dis[S]=0, arc[S]=head[S];
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=head[u]; ~i; i=e[i].nxt) {
int v=e[i].to;
if(e[i].w>eps && dis[v]==infty) {
dis[v] = dis[u]+1;
arc[v] = head[v], q.push(v);
if(v==T) return true;
}
}
}
return false;
}
double dfs(int u,double canFlow) {
if(u==T) return canFlow;
double sumFlow=0, d;
for(int i=arc[u]; ~i; i=e[i].nxt) {
int v=e[i].to; arc[u]=i;
if(e[i].w>eps && dis[v]==dis[u]+1) {
d = dfs(v,min(canFlow,e[i].w));
if(d<eps) dis[v]=infty;
canFlow -= d, sumFlow += d;
e[i].w -= d, e[i^1].w += d;
if(canFlow<eps) break;
}
}
return sumFlow;
}
double dinic() {
double r=0;
while(bfs()) r+=dfs(S,infty);
return r;
}
void addEdge(int u,int v,double w) {
// printf("edge %d %d %f\n",u,v,w);
e[++cnt].to=v, e[cnt].nxt=head[u];
e[cnt].w=w, head[u]=cnt;
e[++cnt].to=u, e[cnt].nxt=head[v];
e[cnt].w=0, head[v]=cnt;
}
bool ok(double mid) {
cnt=-1; memset(head,-1,sizeof(int)*(T+5));
v.clear();
for(int i=1;i<=n;++i)
addEdge(S,i,p[i]),
v.push_back(r[i]),
v.push_back(mid+d[i]);
sort(v.begin(),v.end());
int idx = n;
for(int i=1;i<=m;++i) {
for(int j=1,siz=v.size(); j<siz; ++j) {
if(v[j]-v[j-1]<eps) continue;
++idx; addEdge(idx,T,(v[j]-v[j-1])*i*s[i]);
for(int k=1;k<=n;++k)
if(0.0+r[k]-v[j-1]<eps && v[j]-(mid+d[k])<eps)
addEdge(k,idx,(v[j]-v[j-1])*s[i]);
}
}
return all-dinic()<eps;
}
int main() {
for(int tt=read(9); tt; --tt) {
n=read(9), m=read(9); s[m+1]=0;
all=0; S=n*m*2+n+5, T=S+1;
for(int i=1;i<=n;++i)
p[i]=read(9),r[i]=read(9),d[i]=read(9),all+=p[i];
for(int i=1;i<=m;++i) s[i]=read(9);
sort(s+1,s+m+1,[](int x,int y) { return x>y; });
for(int i=1;i<=m;++i) s[i] -= s[i+1];
double l=0,r=all,mid;
while(r-l>eps) {
mid = (l+r)/2;
if(ok(mid)) r=mid;
else l=mid;
}
printf("%.7f\n",l);
}
return 0;
}
