【Good Bye 2020 E】Apollo versus Pan

题目链接

链接

翻译

题意很简单，让你求题目描述中那个离谱的式子。

题解

大概就是这样做了一下变换

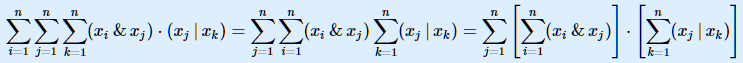
然后我们就可以固定 \(j\)，问题转换成快速求解 \(\sum_{i=1}^n(x_j\ \&\ x_i)\) 和 \(\sum_{i=1}^n(xj\ |\ xi)\)

如果我们设 \(f(i,j)\) 表示 \(i\) 这个数字的二进制从右往左数的第 \(j\) 个 \(bit\) 上的数字。

那么就有如下转换(\(M\)表示 \(x\) 的二进制表示位数最大值),一位一位地进行求解:

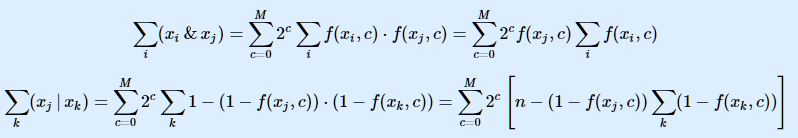
则问题变成求解 \(n\) 个数字的二进制上第 \(j\) 从 \(1\) 到 \(60\) 位的数字之和。

相反数的话用 \(n\) 去减一下就可以了。

时间有点紧张, 运行出来的时候 1993ms _(:з」∠)_。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
 
const int N = 5e5;
const int MOD = 1e9 + 7;
 
int T, n;
int v[N+10][60+10];
int sum[60 + 10];
 
int main() {
	#ifdef LOCAL_DEFINE
		freopen("in.txt", "r", stdin);
	#endif
	ios::sync_with_stdio(0), cin.tie(0);
	cin >> T;
	while (T--){
        cin >> n;
        for (int i = 1;i <= n; i++){
            LL x;
            cin >> x;
            int j = 0;
            while (x > 0){
                v[i][j] = x%2;
                x /= 2;
                j++;
            }
            while (j < 60){
                v[i][j++] = 0;
            }
        }
        for (int j = 0;j < 60; j++){
            sum[j] = 0;
            for (int i = 1;i <= n; i++){
                sum[j] += v[i][j];
            }
        }
        LL ans = 0;
        for (int i = 1;i <= n; i++){
            LL pow2 = 1;
            LL temp1 = 0;
            LL temp2 = 0;
            for (int j = 0;j < 60; j++){
                temp1 += pow2*v[i][j]%MOD*sum[j]%MOD;
                temp2 += pow2*(n-(1-v[i][j])*(n-sum[j])%MOD)%MOD;
                temp1 %= MOD;
                temp2 = (temp2+MOD)%MOD;
                pow2 = pow2*2%MOD;
            }
            temp1 = temp1*temp2%MOD;
            ans = (ans + temp1)%MOD;
        }
        cout << ans << endl;
	}
	return 0;
}