【Good Bye 2020 D】13th Labour of Heracles

题目链接

链接

翻译

让你给一棵树上的边染色，然后对于颜色为 \(k\) 的边, 只保留这些边，形成一个 \(k\) 子图，然后

不是可能会组成很多个联通分量吗？则这个 \(k\) 子图的权重就为所有联通分量的权重最大值。(联通分量的权值为各个节点加和)

你最多可以使用 \(K\) 种颜色的边，\(K\) 从 \(1\) 到 \(n-1\) 变换，让你求出所有子图的权重的累加和的最大值。

题解

假设某种最优方案，出现了其中某一个 \(k\) 子图是由两个或更多联通分量取最大值得到的。

那么我们总是可以将权重和较小的那个联通分量(较小者对答案无贡献)改成相邻颜色的边，让其他子图的权重和更大一些。

所以，最后的最优结果中，每个 \(k\) 子图都只有一个联通分量。

初始的时候，每条边的颜色都相同，每个节点的权重对答案只贡献一次。然后我们在此基础上修改边的颜色，会发现每修改

一条边的话，达到的效果就是将边的一端的节点权重加上去，如下图，我们把边 \(1\) 改成颜色 \(2\)，然后将另外一端颜色

为 \(1\) 的边也改成相邻的 \(2\) (上面那个推论)，这样节点 \(v\) 的权重在最后算累加的时候就又会额外加一次了。

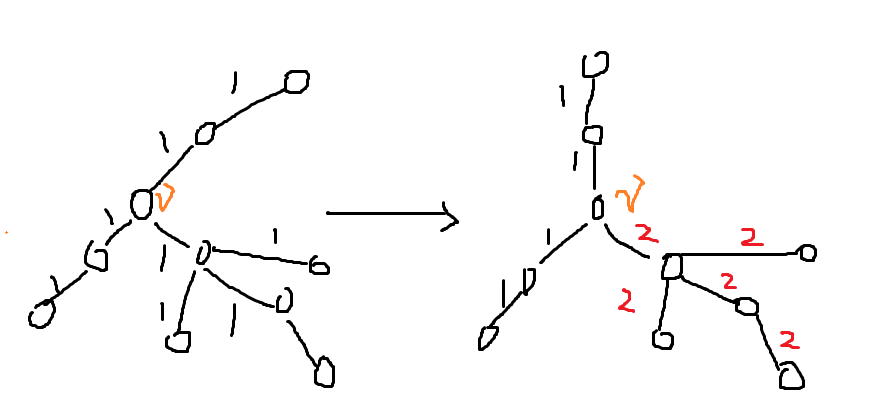
那么我们只需要每次将权重最大的节点的权重累加一次就好了，能累加几次呢?节点的度数减去 \(1\) !为啥要减 \(1\)? 一开始

颜色都一样，已经累加过一次了!

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;

const int N = 1e5;

int T, n;
int du[N + 10],w[N + 10];
multiset<int,greater<int> > myset;

int main() {
	#ifdef LOCAL_DEFINE
		freopen("in.txt", "r", stdin);
	#endif
	ios::sync_with_stdio(0), cin.tie(0);
    cin >> T;
    while (T--){
        myset.clear();
        cin >> n;
        LL ans = 0;
        for (int i = 1;i <= n; i++){
            du[i] = 0;
            cin >> w[i];
            ans += w[i];
        }
        for (int i = 1;i <= n - 1; i++){
            int u, v;
            cin >> u >> v;
            du[u]++;du[v]++;
        }
        for (int i = 1;i <= n; i++){
            for (int j = 1;j < du[i]; j++){
                myset.insert(w[i]);
            }
        }
        cout << ans;

        for (int i = 1;i <= n-2; i++){
            int x = *(myset.begin());
            myset.erase(myset.begin());
            ans += x;
            cout << " " << ans;
        }
        cout << endl;

    }
	return 0;
}