【Codeforces Round #695 (Div. 2) E】Distinctive Roots in a Tree
题目链接
翻译
给你一棵树,树上的每一个节点都带有权值。
让你统计这样的点 \(x\) 的个数,使得以 \(x\) 为根的时候,所有以 \(x\) 开始,以某个节点结束的路径中每个节点的权值
都是唯一的,即每个权值都只出现了一次。
称这样的 \(x\) 为 \(distinctive\ root\), 统计所给的树中这样的 \(distinctive\ root\) 的个数。
题解
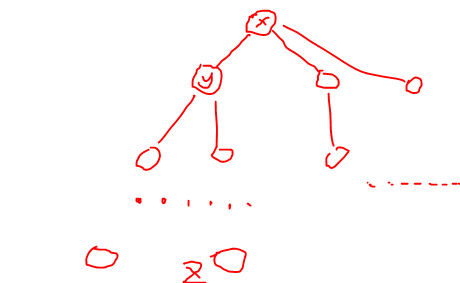
如图,考虑树中的每一个节点 \(x\), 对于它的某一个子树 \(y\) ,我们可以看一下这个子树 \(y\) 下面是否有和 \(x\) 的权值
相同的节点 \(z\),也即 \(a[x]=a[z]\)。如果存在,那么就添加一条特殊的有向边,从 \(x\) 指向 \(y\)。
这代表了,如果存在 \(distinctive\ root\), 那么一定是在 \(y\) 子树中的,因为如果不是在 \(y\) 子树中,而在 \(x\) 其他子树里面。
一定会有一条路径同时经过节点 \(x\) 然后顺着子树 \(y\) 到达节点 \(z\), 而 \(x\) 和 \(z\) 权值相同, 所以这就不满足题意了。
按照这个思路,我们就在原来的树上增加了一些特殊边。
现在对于每一个节点,只要所有的特殊边都指向了它(直接或间接),那么这个节点就是能够成为 \(distinctive\ root\) 的点。
累计答案就行。
具体在实现的时候,对于这个特殊边的添加,我们需要先把每个节点的 \(dfs\) 序求出来,就是先序遍历的时候的顺序。
根据这个 dfs序,我们可以很容易的用 upper_bound 和 lower_bound 得到以某个节点为根的子树下面有多少个权值为 \(x\) 的节点。
不要忘了,我们一开始的时候是以任意一个节点为根进行 \(dfs\) 的,所以除了统计 \(x\) 的子树,还要把 \(x\) 以及它的祖先,也看做
是 \(x\) 的子树,对应的节点 \(z\) 的个数也可以通过总数减子树中数目的方式得到,然后决定是否要连一条特殊边到父节点。
特殊边建立好之后,就可以用一些 \(reroot\) 的方法,在做 \(dfs\) 的时候,根据加加减减动态的维护每个节点有多少条
特殊边直接或间接指向它,对于所有边都指向的点,累加答案即可。
具体的,设 \(dp[i]\) 表示 \(i\) 这个节点有多少条特殊边指向它。然后维护这个数组就好。
特殊边是放在一个集合里面的,这样会比较好(方便)得到某条特殊边是否存在。
吐槽一下,一开始我把 \(dfs\) 序中的某处的 \(in[x]\) 写成了 \(x\),竟然能过 \(7\) 个点:)
代码里写了一点点注释。嗯,好像不是一点点,蛮多的。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 2e5;
int n;
int a[N + 10],par[N+10],in[N+10],out[N+10],timeTip;
vector<int> g[N+10];
map<int,vector<int> > dic;
vector<int> inTimes;
set<pair<int,int> > edgeSet;
//dp[i]表示有多少条边指向 i
int dp[N+10],ans;
void dfs(int x,int fa){
in[x] = ++timeTip;
int len = g[x].size();
for (int i = 0;i < len; i++){
int y = g[x][i];
if (y == fa){
continue;
}
par[y] = x;
dfs(y,x);
}
out[x] = ++timeTip;
}
void setUp(int x){
dp[x] = 0;
int len = g[x].size();
for (int i = 0;i < len; i++){
int y = g[x][i];
if (y == par[x]){
continue;
}
setUp(y);
dp[x] += dp[y] + edgeSet.count({y,x});
}
}
void getAns(int x){
if (dp[x] == (int)edgeSet.size()){
ans++;
}
int len = g[x].size();
for (int i = 0;i < len; i++){
int y = g[x][i];
if (y == par[x]){
continue;
}
dp[x] -= dp[y];
dp[x] -= edgeSet.count({y,x});
dp[y] += dp[x];
dp[y] += edgeSet.count({x,y});
getAns(y);
dp[y] -= dp[x];
dp[y] -= edgeSet.count({x,y});
dp[x] += dp[y];
dp[x] += edgeSet.count({y,x});
}
}
int main(){
#ifdef LOCAL_DEFINE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(0),cin.tie(0);
cin >> n;
for (int i = 1;i <= n; i++){
cin >> a[i];
dic[a[i]].push_back(i);
}
for (int i = 1;i <= n-1; i++){
int x, y;
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs(1,0);
for (pair<int,vector<int> > temp : dic){
if ((int) temp.second.size() == 1){
continue;
}
inTimes.clear();
for (int x:temp.second){
inTimes.push_back(in[x]);
}
sort(inTimes.begin(),inTimes.end());
//以节点 x 为根
for (int x:temp.second){
//统计子树中和它相同的节点的个数(以 1 节点为根时的结果)
int sum = 0;
int len = g[x].size();
for (int i = 0;i < len; i++){
int y = g[x][i];
if (y == par[x]){
continue;
}
//in[y],out[y]
int num = upper_bound(inTimes.begin(),inTimes.end(),out[y])-
lower_bound(inTimes.begin(),inTimes.end(),in[y]);
if (num > 0){
//对应子树中有 a[x],则从对应子树的根节点 y 连一条边到 x
edgeSet.insert({x,y});
}
sum += num;
}
//算上本身。
sum++;
//x的父节点以上的 a[x] 个数
int rest = (int)temp.second.size() - sum;
if (rest > 0){
//如果也有,那么也从x连一条边到 父节点
edgeSet.insert({x,par[x]});
}
}
}
//求出 dp 数组
setUp(1);
//用reroot的方法求出符合要求点数。
getAns(1);
cout << ans << endl;
return 0;
}


