背公式
概率论
概率空间由样本空间 \(S\), 事件域 \(\mathcal F\) 以及概率测度 \(\mathbb P\) 组成.
对于事件 \(B\), 若 \(\mathbb P(B)>0\), 则 \(\mathbb P(A\mid B):=\mathbb P(A\cap B)/P(B)\) 也是概率测度, 称为条件概率.
随机变量是定义在样本空间 \(S\) 上的函数, 若取值至多可数则称为离散的, 要背的有:
- 二项分布 \(\mathrm B(n,p)\): \(\mathbb P(X=k):=\binom nkp^k(1-p)^{n-k},\forall k\in\mathbb Z_{\ge 0}\);
- 泊松分布 \(\pi(\lambda)\): \(\mathbb P(X=k):=\lambda^k\mathrm e^{-\lambda}/k!,\forall k\in\mathbb Z_{\ge 0}\);
- 负二项分布 \(\mathrm{NB}(n,p)\): \(\mathbb P(X=k):=\binom{n+k-1}kp^n(1-p)^k,\forall k\in\mathbb Z_{\ge 0}\);
存在概率密度函数的随机变量称为连续的, 要背的有:
- 均匀分布 \(\mathrm U(a,b)\): \(f(x):=1/(b-a),\forall x\in[a,b]\);
- 伽马分布 \(\Gamma(\alpha,\lambda)\): \(f(x):=x^{\alpha-1}\lambda^\alpha\mathrm e^{-\lambda x}/\Gamma(\alpha),\forall x\ge 0\);
- 指数分布 \(\mathrm{Exp}(\lambda)=\Gamma(1,\lambda)\);
- 正态分布 \(\mathrm N(\mu,\sigma^2)\): \(f(x):=\frac 1{\sigma\sqrt{2\pi}}\mathrm e^{-(x-\mu)^2/2\sigma^2},\forall x\in\mathbb R\);
- 卡方分布 \(\chi^2(n)=\Gamma(n/2,1/2)\);
- t 分布 \(\mathrm t(n)\): \(f(x):=\frac{\Gamma((n+1)/2)}{\sqrt{n\pi}\Gamma(n/2)}(1+x^2/n)^{-(n+1)/2},\forall x\in\mathbb R\);
- F 分布 \(\mathrm F(n_1,n_2)\): \(f(x):=n_1^{n_1/2}n_2^{n_2/2}x^{n_1/2-1}(n_2+n_1x)^{-(n_1+n_2)/2}/\mathrm B(n_1/2,n_2/2),\forall x>0\).
- 多元正态分布 \(\mathrm N(\boldsymbol\mu,B)\): \(f(\boldsymbol x):=(2\pi)^{-n/2}|B|^{-1/2}\exp(-\frac 12(\boldsymbol x-\boldsymbol a)^\mathrm TB^{-1}(\boldsymbol x-\boldsymbol a))\).
连续随机变量的函数分布: 若 \(Y=g(X)\), 则 \(f_Y(y)|\mathrm dy|=\int_{g(x)=y}f_X(x)|\mathrm dx|\), 要背的有:
- 若 \(X,Y\) 独立, \(Z:=X+Y\), 则 \(f_Z=f_X*f_Y\);
- 设 \(X\) 表示 \(n\) 次独立试验中概率为 \(p\) 的事件发生的次数, 则 \(X\sim\mathrm B(n,p)\), 从而满足可加性;
- 设 \(X\) 表示重复独立实验直到概率为 \(p\) 的事件发生 \(n\) 次, 不发生的次数, 则 \(X\sim\mathrm{NB}(n,p)\), 从而满足可加性;
- 泊松分布满足可加性;
- 设 \(t\) 时间内事件发生次数服从 \(\pi(\lambda t)\), 则发生第 \(n\) 次的时间服从 \(\Gamma(n,\lambda)\), 从而满足可加性;
- 设 \(X\) 是 \(n\) 个独立 \(\mathrm N(0,1)\) 的平方和, 则 \(X\sim\chi^2(n)\), 从而满足可加性.
- 若 \(Z:=X/Y\), 则 \(f_Z(z)=\int_{-\infty}^\infty|y|f(yz,y)\mathrm dy\);
- 若 \(X\sim\mathrm N(0,1)\), \(Y\sim\chi^2(n)\) 独立, 则 \(\frac{X}{\sqrt{Y/n}}\sim\mathrm t(n)\);
- 若 \(X\sim\chi^2(n_1)\), \(Y\sim\chi^2(n_2)\) 独立, 则 \(\frac{X/n_1}{Y/n_2}\sim\mathrm F(n_1,n_2)\).
- 二元标准正态分布的极坐标满足 \(R^2\sim\mathrm{Exp}(1/2)\), \(\Theta\sim\mathrm U(0,2\pi)\).
- 多元正态分布的边缘分布和线性变换也为正态分布. 具体地, 若 \(\boldsymbol X\sim\mathrm N(\boldsymbol a,B)\), 则 \(A\boldsymbol X+\boldsymbol b\sim\mathrm N(A\boldsymbol a+\boldsymbol b, ABA^\mathrm T)\). 特别地, 正交变换不改变协方差矩阵.
随机变量列的收敛有:
- 依 r 阶矩收敛: \(\mathbb E[|X_n-X|^r]\to 0\), 记作 \(X_n\xrightarrow{L^r}X\);
- 依概率收敛: 对任意 \(\varepsilon>0\) 都有 \(\mathbb P(|X_n-X|>\varepsilon)\to 0\), 记作 \(X_n\xrightarrow p X\);
- 几乎必然收敛: 对任意 \(\varepsilon>0\) 都有 \(\mathbb P(\sup_{m\ge n}|X_m-X|>\varepsilon)\to 0\), 记作 \(X_n\xrightarrow{a.s.}X\);
- 依分布收敛: 对任意 \(a\in\mathbb R\) 都有 \(\mathbb P(X_n\le a)\to\mathbb P(X\le a)\), 记作 \(X_n\xrightarrow{d}X\).
它们之间的关系如下:
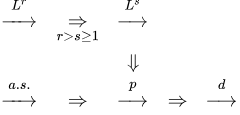
要背的定理有:
- Markov 不等式: 若 \(X\ge 0\), 则 \(\mathbb P(X\ge\varepsilon)\le\mathbb E(X^k)/\varepsilon^k\);
- 强大数定律: 设 \(\{X_n\}_n\) 独立同分布, 期望 \(\mu\) 存在, 则 \(S_n/n\xrightarrow{a.s.}\mu\);
- 中心极限定理: 设 \(\{X_n\}_n\) 独立同分布, 期望 \(\mu\) 和方差 \(\sigma^2\) 存在, 则 \((S_n-n\mu)/\sqrt{n}\sigma\xrightarrow d\mathrm N(0,1)\).
数理统计
统计量是样本的函数, 其不依赖于未知参数. 衡量标准有:
- 无偏性: \(\mathbb E(\widehat\theta)=\theta\);
- 相合性: \(\widehat{\theta_n}\xrightarrow p\theta\);
- 有效性: 若 \(\mathrm D(\widehat{\theta_1})\le\mathrm D(\widehat{\theta_2})\), 且存在 \(\theta\in\Theta\) 使得不等号成立, 则称 \(\widehat{\theta_1}\) 比 \(\widehat{\theta_2}\) 有效.
点估计的构造方法有:
- 矩法: 求出参数关于 \(k\) 阶矩的函数, 然后代以样本 \(k\) 阶矩;
- 极大似然估计: 用似然函数的 argmax 作为参数的估计.
区间估计的构造方法: 用枢轴量解出参数的范围.
对于单个正态总体 \(\mathrm N(\mu,\sigma^2)\):
- 若 \(\sigma^2\) 已知, 估计 \(\mu\), 则 \(\sqrt n(\overline X-\mu)/\sigma\sim\mathrm N(0,1)\);
- 若 \(\sigma^2\) 未知, 估计 \(\mu\), 则 \(\sqrt n(\overline X-\mu)/S\sim\mathrm t(n-1)\);
- 若 \(\sigma^2\) 未知, 估计 \(\sigma^2\), 则 \((n-1)S^2/\sigma^2\sim\chi^2(n-1)\).
对于两个正态总体 \(\mathrm N(\mu_1,\sigma_1^2)\) 和 \(\mathrm N(\mu_2,\sigma_2^2)\):
- 若 \(\sigma_1^2,\sigma_2^2\) 已知, 估计 \(\mu_1-\mu_2\), 则 \(\dfrac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}\sim\mathrm N(0,1)\);
- 若 \(\sigma_1^2=\sigma_2^2\) 未知, 估计 \(\mu_1-\mu_2\), 则 \(\dfrac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{S_w\sqrt{n_1^{-1}+n_2^{-1}}}\sim\mathrm t(n_1+n_2-2)\), 其中 \(S_w^2:=\dfrac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}\);
- 估计 \(\sigma_1^2/\sigma_2^2\), 则 \(\dfrac{S_1^2/S_2^2}{\sigma^2_1/\sigma_2^2}\sim\mathrm F(n_1-1,n_2-1)\).
对于其他情况, 使用中心极限定理近似.
假设检验: 设原假设 \(H_0\) 为希望证否的假设, 当所观测的样本足够显著时将其推翻. 通常把区间估计的枢轴量中所估计的参数替换为已知量即得假设检验的统计量.
线性回归: 对于模型 \(Y=\alpha+\beta X+\varepsilon\), \(\varepsilon\sim\mathrm N(0,\sigma^2)\) 给出的样本 \(\{(x_i,y_i)\}_{i=1}^n\), 极大似然估计 (最小二乘) 给出的统计量为
其中 \(s_{xx}=\sum_i(x_i-\overline x)^2\), \(s_{xy}=\sum_i(x_i-\overline x)(y_i-\overline y)\).
若要做显著性检验, 则令 \(H_0\) 为 \(\beta=0\), 令 \(\mathrm{SSE}:=\sum_i(y_i-\widehat{y_i})^2\) 为残差平方和, \(\mathrm{SSR}:=\sum_i(\widehat{y_i}-\overline y)^2\) 为回归平方和, 则 \(\mathrm{SSE}/\sigma^2\sim\chi^2(n-2)\), 而当 \(\beta=0\) 时 \(\mathrm{SSR}/\sigma^2\sim\chi^2(1)\), 否则 \(\mathrm{SSR}\) 会偏大, 取统计量 \(F:=\frac{\mathrm{SSR}}{\mathrm{SSE}/(n-2)}\sim\mathrm F(1,n-2)\), 拒绝域 \(W:=\{F>\mathrm F_\alpha(1,n-2)\}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号