大学生物复习

搜索

搜索问题的定义包含初始状态 \(S_0\), 可选动作 \(\mathrm{Action}(S)\), 状态转移模型 \(\mathrm{Result}(S,a)\), 目标状态 \(T\), 路径花费 \(\mathrm{Cost}:\mathrm{Path}\to\mathbb R\).

搜索算法使用搜索树表示过程, 闭节点集表示所有已探索节点, 开节点集表示所有待探索节点. 分为树搜索 (可能重复探索) 和图搜索 (记录闭节点集, 判重使得不重复探索).

无信息搜索有 dfs 和 bfs 以及一致代价搜索 (先扩展花费最小的结点).

有信息搜索有 A* 算法, 启发式函数 \(h\) 可采纳 (不会超过实际花费) 则树搜索 A* 最优, 一致 (满足三角不等式) 则图搜索 A* 最优.

局部搜索: 不关心路径, 利用状态估值函数找解.

  • 爬山法: 从初始状态出发, 向更好的邻居状态移动, 策略有:
    • 最陡爬山法: 选择邻居中最优的. 容易陷入局部最优.
    • 随机平移: 估值相等时随机选择平移. 有助于跳出肩状平台.
    • 随机爬山法: 选择随机的更好邻居. 收敛速度变慢.
    • 第一选择爬山法: 选择第一个更好邻居. 减少计算量.
    • 随机重启: 陷入局部最优时重启.
  • 模拟退火: 以 \(\exp(\Delta E/T)\) 的概率转移到更劣邻居.
  • 遗传算法是随机束搜索算法的变种.

连续空间搜索: 梯度下降 (不可微就近似算一个).

对抗搜索: 完全信息游戏可以建模为搜索问题.

极大极小搜索: 假设各方采取最优策略, 使用 dfs 计算. 效率低, 但可以扩展到多人非零和游戏.

\(\alpha\text-\beta\) 剪枝: 维护 \(\alpha\) 和 \(\beta\) 表示当前子树能更新策略的权值下界/上界, 当 \(\alpha\ge\beta\) 时 return.

int alpha_beta(int u, int alph, int beta, bool is_max) {
  if (!son_num[u]) return val[u];
  if (is_max) {
    for (int i = 0; i < son_num[u]; ++i) {
      int d = son[u][i];
      alph = max(alph, alpha_beta(d, alph, beta, is_max ^ 1));
      if (alph >= beta) break;
    }
    return alph;
  } else {
    for (int i = 0; i < son_num[u]; ++i) {
      int d = son[u][i];
      beta = min(beta, alpha_beta(d, alph, beta, is_max ^ 1));
      if (alph >= beta) break;
    }
    return beta;
  }
}

MCTS 算法: 迭代地构建搜索树, 每次迭代更新估值包含以下四个步骤,

  • 选择: 根据树策略找到需要扩张的节点, 例如结合 UCB 公式 Upper Confidence Bound 就得到 UCT 算法 Upper Confidence Bound Apply to Tree: 设常数 \(c\), 从当前结点 \(v\) 递归到

    \[\mathrm{argmax}_{v'\in\mathrm{child}(v)}\frac{Q(v')}{N(v')}+c\sqrt{\frac{2\ln N(v)}{N(v')}}. \]

  • 扩张: 根据可选操作添加叶节点.
  • 模拟: 根据默认策略进行价值评估.
  • 反向传播: 根据模拟结果更新祖先结点的信息.

强化学习

智能体与环境的交互过程可以建模为 Markov 决策过程, 包含状态集合 \(S\), 动作集合 \(A\), 状态转移函数 \(P(s,a,s'):=\mathbb P(s'|s,a)\), 奖励函数 \(R(s,a,r):=\mathbb P(r|s,a)\).

设折扣因子 \(\gamma\in(0,1)\), 智能体的目标是最大化累积收益值 \(G_t:=\sum_{k=0}^\infty\gamma^kR_{t+k}\) 的期望. 求解这个问题可以使用动态规划方法: 对于策略 \(\pi\), 定义状态价值函数 \(V_\pi(s)\) 表示初始状态为 \(s\) 时的累积收益值期望, 动作价值函数 \(Q_\pi(s,a)\) 表示初始状态为 \(s\), 接下来一步采取动作 \(a\) 时的累计收益值期望, 则有 Bellman 期望方程:

\[\begin{aligned} V_\pi(s)&=\sum_a\pi(a|s)\cdot Q_\pi(s,a), \\ Q_\pi(s,a)&=\sum_{s',r}p(s',r|s,a)\cdot(r+\gamma V_\pi(s')). \end{aligned} \]

显然最优策略是选择动作价值最高的动作, 故最优状态价值 \(V^*(s)\) 和最优动作价值 \(Q^*(s,a)\) 满足如下的 Bellman 最优方程:

\[\begin{aligned} V^*(s)&=\max_aQ^*(s,a), \\ Q^*(s,a)&=\sum_{s',r}p(s',r|s,a)\cdot(r+\gamma V^*(s')). \end{aligned} \]

当 \(P,R\) 已知时, 求解这个方程有如下方法:

  • 值迭代: 根据方程迭代更新 \(V^*\) 函数.
  • 策略迭代: 维护策略 \(\pi\), 每次迭代求解 \(V^\pi\), 然后更新 \(\pi\).

当 \(P,R\) 未知时, 需要通过采样方法逼近, 按是否自举 bootstrap 分为蒙特卡洛和时序差分两类. 通常使用 \(\varepsilon\)-贪心方法进行采样.

  • SARSA: 时序差分, 每次根据下一动作更新函数 \(Q(s,a)\).
  • Q-Learning: 时序差分, 维护函数 \(Q(s,a)\), 但不考虑下一动作而直接取最大 \(Q\) 值.

在策略可微的情况下可以对策略做梯度下降, 称为策略梯度方法, 但是应该不考.

机器学习

机器学习算法基于经验提升模型在某些任务上的表现.

例如有监督, 无监督, 半监督, 弱监督, 强化学习. 详见 AI 系统部分.

线性回归: \(\|Av-w\|_2\) 最小当且仅当 \(A^\mathrm TAv=A^\mathrm Tw\).

Lasso 回归: 假设模型参数符合 Laplace 分布, 鼓励模型参数的解具有稀疏性.

Ridge 回归: 假设模型参数符合正态分布, 鼓励模型参数的解取值较小.

广义线性模型: 套一层单调可微函数, 例如 Logistic 回归.

多元 Logistic 回归: 多分类问题, 套 softmax 函数.

K-近邻分类器: 最近的 \(K\) 个邻居取众数, 是无参方法, 超参数有 \(K\) 和度量函数.

K-mean 聚类: 随机撒 \(K\) 个中心, 每次把每个点分配给距离最近的中心, 然后更新中心为平均值, 不断重复. 是无参方法, 超参数有 \(K\) 和度量函数, 可能还有初始中心的选择方法.

密度估计, 降维: 不知道是啥, 总之是无监督的.

深度学习

神经元 \(z:=\boldsymbol w^T\boldsymbol x+b\), 偏值 \(b\) 增大了输出范围.

激活函数为神经网络层的输出提供非线性性.

  • Sigmoid 函数 \(\sigma(z)=\dfrac 1{1+\mathrm e^{-z}}\), 值域 \([0,1]\), 通常用于表示概率.
  • Tanh 函数 \(\tanh z=\dfrac{\mathrm e^z-\mathrm e^{-z}}{\mathrm e^z+\mathrm e^{-z}}\), 值域 \([-1,1]\), 通常用于回归任务.
  • ReLU 函数 \(f(z)=\max(0,z)\), 用于中间层, 解决梯度消失 gradient vanish 问题.
  • Leaky ReLU 函数 \(f(z)=\begin{cases}\alpha z,&z<0, \\ z,&z\ge 0\end{cases}\), 使得负输出的信息可以在激活值上体现.
  • Softmax 函数 先逐位 \(\exp\) 然后归一化, 用于多分类任务中表示概率.

单层网络无法处理不具有线性可分性的问题, 多层感知器 multi-layer
perceptron 可以处理更复杂的输入数据, 具有更好的表达能力.

损失函数 loss function 用于量化网络的预测输出 predicted output 与训练数据输出 ground truth 之间的误差.

  • 交叉熵损失函数 Cross-Entropy Loss \(\mathcal L(\boldsymbol a,\boldsymbol y)=-\sum_iy_i\log(a_i)\).
  • 均方误差 Mean Squared Error \(\mathcal L(\boldsymbol a,\boldsymbol y)=\sum_i(a_i-y_i)^2\).
  • 平均绝对误差 Mean Absolute Error \(\mathcal L(\boldsymbol a,\boldsymbol y)=\sum_i|a_i-y_i|\).

优化神经网络的过程, 是通过更新其参数来使得误差尽可能小.

梯度下降 gradient descent \(\boldsymbol\theta:=\boldsymbol\theta-\alpha\frac{\partial\mathcal L}{\partial\boldsymbol\theta}\).

随机梯度下降 stochastic ~ 每次更新随机选取一批 batch 数据来计算误差, 覆盖一次整个训练数据集称为一轮 epoch.

正则化 normalization 在训练过程中用以减缓过拟合 over-fitting.

  • 数据增强 Data Augmentation 通过对数据的处理获得更多数据.
  • 提前停止法在网络开始过拟合的时候, 提前停止训练.
  • 权重衰减 Weight Decay 对权重予以 \(L^1\) 或 \(L^2\) 范数的惩罚.
  • Dropout 在训练过程中按比例 \(p\) 随机对隐藏输出置 \(0\), 断开神经元的连接.

对于 kernel_size 为 \(k\), padding 为 \(p\), 步长为 \(s\) 的卷积层, 若输入大小为 \(w\), 则输出大小 \(n=\lfloor(w-k+2p)/s\rfloor+1\).

对于卷积神经网络, 设第 \(i\) 层的 kernel_size 为 \(k_i\), 步长为 \(s_i\), dilation 为 \(d_i\), 考虑如何计算每一层的感受野大小 \(\mathrm{rf}_i\): 不妨设 \(d_i=1\), 否则令 \(k_i:=1+(k_i-1)d_i\); 则 \(\mathrm{rf}_0=1\), \(\mathrm{rf}_i=\mathrm{rf}_{i-1}+(k_i-1)\prod_{j=1}^{i-1}s_i\).

池化层 pooling 压缩数据量, 减小过拟合 (增强平移不变性).

CNN 架构选讲:

  • 2012 年, AlexNet 在 ImageNet 数据集上相较于之前的方法取得了 \(10\%\) 的性能提升.
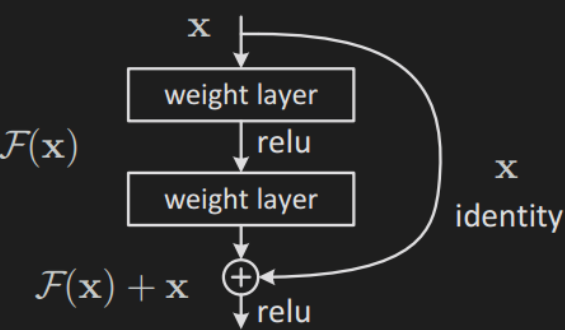
  • ResNet 使用残差块解决深层网络的梯度消失问题.
  • SqueezeNet 是一个轻量型网络, 包含三个卷积层, 分为 squeeze 和 expand 两部分, 分别压缩和扩展数据的通道数.
  • MobileNet 的核心是深度可分离卷积 Depthwise Separable Convolution, 将一个完整的卷积运算分解为深度卷积和逐点卷积两部分.
  • ShuffleNet 分组卷积, 再打乱通道进行信息合并.

反卷积 Transposed Convolution 在输入数据之间插入 \(0\), 从而扩大输出大小.

CNN 在计算机视觉中的应用:

目标检测: 找出图像中所有目标, 确定它们的类别和位置; 评估效果使用交并比和平均精确度 (Precision-Recall 曲线下方的面积).

  • R-CNN: 使用选择性搜索算法 Selective Search 从图像中提取候选区域, 调整为给定的固定大小, 输入 CNN 以提取图像特征, 通过 SVM 进行分类, 使用非极大值抑制 Non-Maximum Suppression 去除重复的边界框, 使用神秘回归器微调边界框. 局限性有:
    • 太慢了.
    • 调整候选区域的尺寸会导致宽度和高度的比例变化，从而影响分类的准确性.
    • 非端到端训练 / 训练步骤繁琐.
  • SPPNet 的改进: 提出了空间金字塔池化 Spatial Pyramid Pooling, 使得网络可以输入任意大小的图片而产生相同大小的输出; 将整个图像输入到CNN中以获得全局特征, 并在全局特征上获得每个区域的特征.
  • Fast R-CNN 的改进: 提出了感兴趣区域池化层 Region of Interest Pooling, 这是一种简化的空间金字塔池化方法, 只使用一个池化尺寸; 并使用多任务损失来近似端到端 (单阶段) 训练.
  • Faster R-CNN 的改进: 使用区域提议网络 Region Proposal Network 替换选择性搜索.
  • YOLO 算法的改进: 使用全卷积网络 Fully Convolutional Network 替换区域提议网络, 直接输出类别标签和位置信息. 局限性为难以检测小物体.
  • YOLO v2 算法: 提高网格分辨率, 为每个网格单元预定义多个提议区域.
  • SSD 算法 Single Shot Multibox Detector: Google 推出的不知道啥玩意.

图像分割: 将图像细分为多个图像子区域, 简化或改变图像的表示形式, 使得图像更容易理解和分析. 评估效果使用 Dice 系数 \(\frac{2|A\cap B|}{|A|+|B|}\) 而不使用交叉熵 (面积大的物体对损失的权重大, 导致对于分割小物体的性能较差).

通常使用全卷积网络: 由编码器和解码器构成, 编码器使用池化和步幅卷积进行下采样, 解码器使用反卷积进行上采样. 增加跳跃连接将低级别特征带到解码过程中, 从而提高了分割细节模式的性能.

可采用的技巧有镜像填充和损失加权.

语义分割: 对图像中的每个像素分配一个类别标签.

实例分割: 目标检测 + 语义分割.

姿态估计: 检测图像中的人物姿态.

  • 自顶向下: 先进行目标检测, 然后提取姿态信息 (关键点). 例如 CPM.
  • 自底向上: 先检测出关键点, 然后划分为不同的人.
    例如 OpenPose. PPN 结合了 YOLO 和 OpenPose, 将姿态估计化为目标检测问题, 但在人群密集或人物尺度差异较大的情况下表现较差.

人脸识别: 目标检测 + 人脸对齐 + 身份识别.

开放式人脸识别: 模型是固定的, 无关于输入的人脸. 例如预训练编码器, 通过比较输入的待查询特征向量与数据库中的已知特征向量的距离来进行身份识别.

生成式模型: 给定训练数据, 学习其概率分布从而进行采样.

朴素 GAN: 训练判别器 \(D\) 使得 \(\mathcal L_D:=-\mathbb E_{\boldsymbol x\sim p_\mathrm{data}}[\log D(\boldsymbol x)]-\mathbb E_{\boldsymbol z\sim p_\mathrm z}[\log(1-D(G(\boldsymbol z))]\) 尽可能小, 训练生成器 \(G\) 使得 \(\mathcal L_G:=-\mathbb E_{\boldsymbol z\sim p_\mathrm z}[\log D(G(\boldsymbol z))]\) 尽可能小.
每一轮训练采样一批 \(\boldsymbol z\) 和 \(\boldsymbol x\), 更新判别器 \(D\), 然后更新生成器 \(G\).

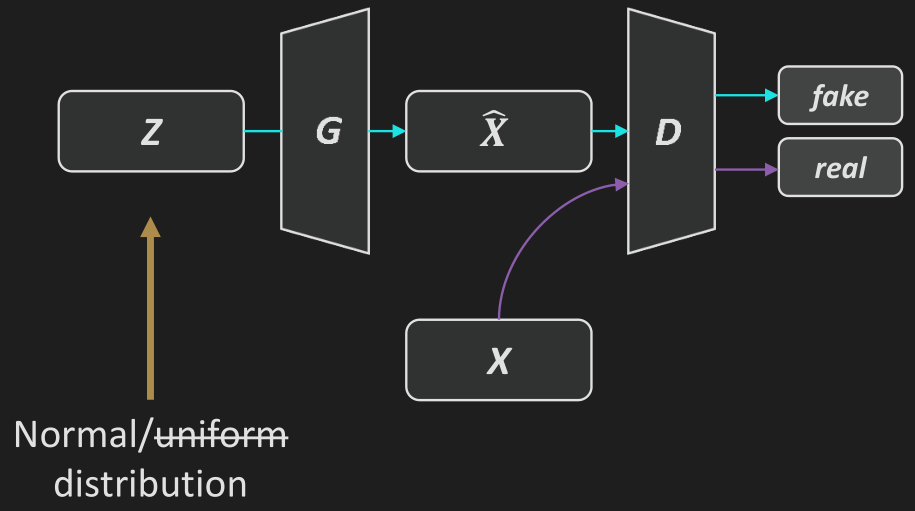
DCGAN: 对于图像生成任务, 使用 CNN 搭建判别器和生成器然后大力调参.

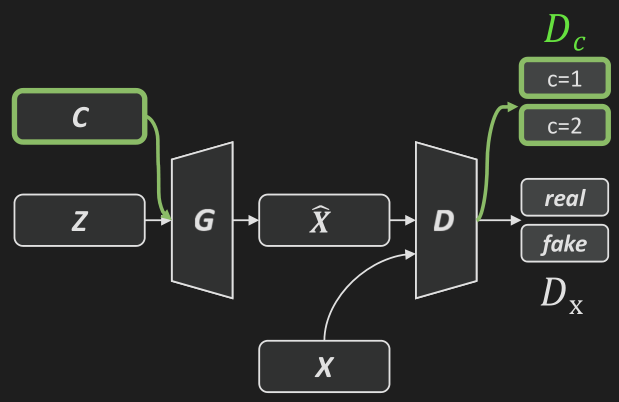
Conditional GAN: 辅助分类器生成对抗网络: TODO.

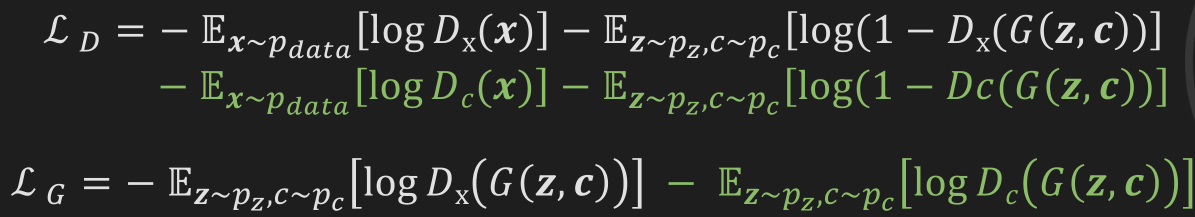
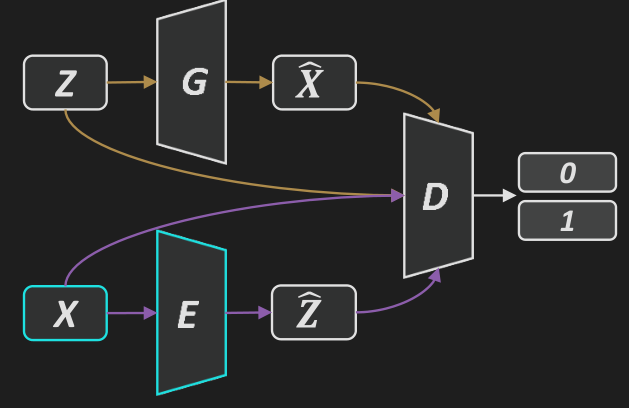
BiGAN: 带编码器的生成对抗网络.

词嵌入: 用向量表示单词. 现有的算法通过阅读大量文本文档来学习词嵌入表, 比较上下文来找到相似的单词, 这是一种自监督学习方法.

  • 连续词袋模型 Continuous Bag-of-Words: 根据上下文预测中间的词.
  • Skip Gram: 根据中间的词预测上下文. 负样本太多, 只能随机采样, 这种方法被称为噪声对比估计 Noise-Contrastive Estimation.

循环神经网络: 将前一个时间的信息传递给下一个时间, 从而处理序列信息.

LSTM: 朴素神经网络难以捕捉长期时间关联,

class LSTM(nn.Module):
	def __init__(self, ins, hs):
		super().__init__()
		self.hs = hs
		self.W = nn.Parameter(torch.Tensor(ins, hs * 4).to(device))
		self.U = nn.Parameter(torch.Tensor(hs, hs * 4).to(device))
		self.bias = nn.Parameter(torch.Tensor(hs * 4).to(device))

		stdv = 1.0 / np.sqrt(hs)
		for weight in self.parameters():
			weight.data.uniform_(-stdv, stdv)
		 
	def forward(self, x):
		hs = self.hs
		bs, seqs, _ = x.size()
		hidden_seq = []
		h_t = c_t = torch.zeros(bs, hs).to(device)

		for t in range(seqs):
			x_t = x[:, t, :]
			gates = x_t @ self.W + h_t @ self.U + self.bias
			i_t = torch.sigmoid(gates[:, :hs])
			f_t = torch.sigmoid(gates[:, hs:hs*2])
			g_t = torch.tanh(gates[:, hs*2:hs*3])
			o_t = torch.sigmoid(gates[:, hs*3:])
			c_t = f_t * c_t + i_t * g_t
			h_t = o_t * torch.tanh(c_t)
			hidden_seq.append(h_t.unsqueeze(0))

		hidden_seq = torch.cat(hidden_seq, dim=0)
		return hidden_seq.transpose(0, 1).contiguous()

Transformer 模型由 \(N\) 个编码器和 \(N\) 个解码器构成.

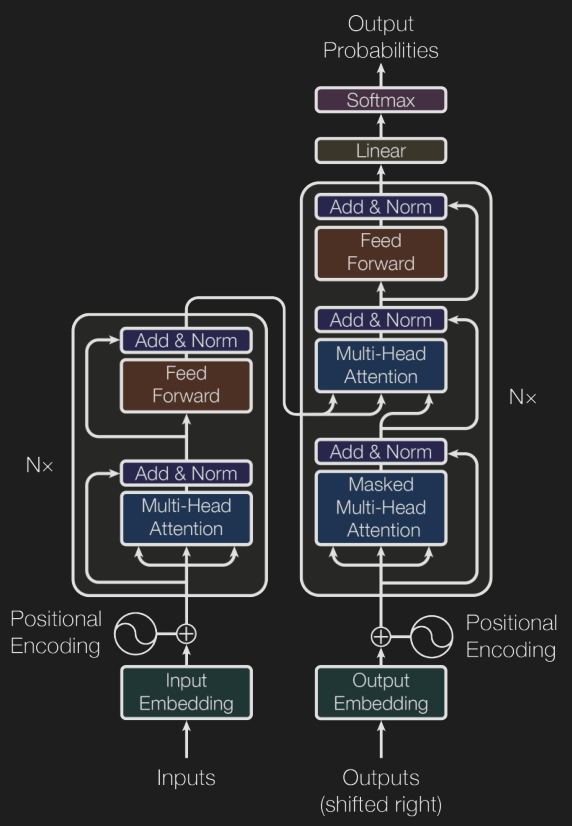
  • 位置编码: 使用向量表达位置, 相近的位置对应的向量相似度也更大, 例如选取常数 \(C\), 令

    \[\begin{aligned} \mathrm{PE}(\mathrm{pos},2i)&:=\sin(\mathrm{pos}/C^{2i/d}), \\ \mathrm{PE}(\mathrm{pos},2i+1)&:=\cos(\mathrm{pos}/C^{2i/d}). \end{aligned} \]

  • 源输入序列经过嵌入层的处理得到词嵌入, 并加入位置编码, 得到最终的输入向量.
  • 注意力机制: 给定一些 Key-Value 对, 对于每个 Query, 利用 Query 与每个 Key 的相似度对 Value 进行加权平均. 例如 (缩放)点积注意力: 设 Key 和 Query 都是 \(d_\mathrm K\) 维向量, 作为行向量排列为矩阵 \(Q\) 和 \(K\), 则 \(QK^\mathrm T\) 中第 \(i\) 行第 \(j\) 列的元素表示第 \(i\) 个 Query 与第 \(j\) 个 Key 的点积 (相似度), 逐行做 softmax 以归一化, 乘上 Value 矩阵 \(V\) 计算加权平均, 即

    \[\mathrm{Attention}(Q,K,V):=\mathrm{softmax}\left(\frac{QK^\mathrm T}{\sqrt{d_\mathrm K}}\right)V. \]

  • 自注意力机制: Key, Value, Query 都是同一个东西, 从而进行信息的糅合.
  • 多头注意力: 将每个向量切成 \(h\) 份, 分别做注意力机制, 最后拼接起来过一个线性层.
  • 解码器的输入称为目标序列, 是模型之前生成的单词.
  • 掩蔽多头注意力: 还没生成的单词就没有, 别算上了.
  • 层规范化: 将每层的输出值变换到均值为 \(0\), 方差为 \(1\) 的范围内.
  • 逐位前馈网络: 每个向量分别过一个两层 MLP.

AI 系统

AI 系统组成部分: 数据获取, 数据处理, 建模与调参, 系统部署以及持续维护.

数据获取:

  • 学术论文数据集: 质量较高, 可与其他论文对比, 但选择少, 规模相对较小.
  • 企业/竞赛数据集: 更贴近实际应用, 但只有热门问题.
  • 采集原始数据: 数据量大但质量不可控.
  • 使用生成器: 例如使用现有模型生成图片, 或通过模拟器生成.

数据标注:

  • 半监督学习: 利用已经标记的部分数据训练一个简单模型, 用这个模型预测的结果, 选择置信度高样本的预测值作为伪标签, 把这些样本加入训练集, 重新训练.
  • 主动学习: 选择不会做的数据问人类.
  • 弱监督学习: 通过自动化或者半自动化生成的标签.
  • 自监督学习: 利用数据自身构造预测标签.

数据清理: 消除错误数据, 例如

  • 异常值: 数据值与其他观测值显著不同的数据点.
  • 规则 / 模式违反: 违反先验知识的数据.

可以直接删除, 也可以用某种方式补全.

特征选择:

  • 过滤法: 根据特征本身的属性进行选择, 例如相关系数, 互信息. 简单但无法考虑特征之间的相关性, 容易选取冗余特征.
  • 嵌入法: 利用模型训练过程选取特征, 例如 \(L^1\) 正则化. 可以考虑特征相关性但特定于某些模型.
  • 包装法: 将特征选择看作搜索问题, 通过评估模型效果来选择特征. 可以考虑特征相关性并针对任意模型, 但是太慢且容易过拟合.

模型的总偏差分为系统误差 Bias 和训练集敏感度 Variance 两部分.

集成学习: 降低 Bias 和 Variance 的有效手段, 例如

  • Bagging: 并行学习 \(n\) 个模型, 对预测值取平均, 从而降低 Variance.
  • Boosting: 顺序学习 \(n\) 个模型, 重点关注预测值偏差较大的样本, 组合减少误差, 从而降低 Bias (应该也可以降低 Variance).
  • Stacking: 并行学习 \(n\) 个模型, 训练一组参数用于合并结果, 从而降低 Variance.

HPO 任务: 通过搜索找到一组好的超参数. 例如

  • 黑盒优化: 将训练过程视为黑盒.
  • 多粒度优化: 简化训练过程.

NAS 任务: 构建一个好的神经网络模型. 例如

  • 强化学习: 速度慢.
  • One-shot 方法: 将架构学习和模型参数学习结合起来, 构建和训练一个模型来展示各种架构.
  • 可微架构搜索: 为每层定义多个候选运算, 学习加权系数进行平均, 选取权重最大的候选运算.

部署模型后根据改进空间, 出现频率, 重要性决定优化的工作优先级, 优化方法有收集更多数据, 使用数据增强获得更多数据, 提高数据质量.

底层实现

深度学习底层架构分为硬件层 (CPU/GPU), 内核层 (C/C++ 实现), 低阶接口 (矩阵和算子), 中阶接口 (网络层, 优化器, 损失函数等模块), 高阶接口 (模型, 训练过程).

计算图是一个 DAG, 结点表示算子, 边表示 Tensor 状态和计算间的依赖关系.

生成方式分为静态 (编译时) 和动态 (运行时) 两种, 静态对计算机友好而对程序员不友好, 动态反之.

调度顺序: 是个拓扑序就行.

posted @ 2023-06-11 15:09  mizu164  阅读(152)  评论(1)  编辑  收藏  举报