2020.11刷题记录

朱刘算法

这是求最小树形图的经典做法 😃

对于所有点，每次找到一条进入它的最小边，这些边如果不形成环则得到答案，否则环上至多断一条边，于是将这个环缩点，答案加上环上边权和，进入这个环的边权减去在环上进入对应点的边权，然后重复这个过程。正确性~~挺显然的~~，时间复杂度 \(O(nm)\)。

可以使用左偏树+并查集优化。用可并堆维护进入每个点的边权，遍历所有点，若当前点还没确定父亲，则可以一直通过进入当前点的最小边~~往上爬~~，形成一个经典 \(\rho\) 形，按上面所说的方法处理环即可。每次遍历一个 \(\rho\) 将环缩点，将~~手柄(?)~~确定父亲，因此时间复杂度是 \(O(m\log m)\)。

~~（在模板题里跑得比暴力慢）~~

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 11111;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, r, cnt, ans, rt[N], fa[N], is[N], pre[N], ch[N][2], val[N], dis[N], to[N], tag[N];
void pushtag(int x, int v){val[x] += v; tag[x] += v;}
void pushdown(int x){
    if(tag[x]){
        int l = ch[x][0], r = ch[x][1];
        if(l) pushtag(l, tag[x]);
        if(r) pushtag(r, tag[x]);
        tag[x] = 0;
    }
}
void merge(int &x, int y){
    if(!x || !y){x += y; return;}
    if(val[x] > val[y]) swap(x, y);
    tag[y] -= tag[x]; val[y] -= tag[x];
    merge(ch[x][1], y);
    if(dis[ch[x][0]] < dis[ch[x][1]]) swap(ch[x][0], ch[x][1]);
    dis[x] = dis[ch[x][1]] + 1;
}
int getfa(int x){return x == fa[x] ? x : fa[x] = getfa(fa[x]);}
void comb(int x, int y){
    x = getfa(x); y = getfa(y);
    if(x != y){fa[x] = y; merge(rt[y], rt[x]);}
}
void pop(int &x){pushdown(x); merge(ch[x][0], ch[x][1]); x = ch[x][0];}
int top(int x){
    while(rt[x] && getfa(to[rt[x]]) == x) pop(rt[x]);
    if(!rt[x]){puts("-1"); exit(0);}
    to[rt[x]] = getfa(to[rt[x]]); return rt[x];
}
int main(){
    read(n); read(m); read(r); is[r] = r; cnt = n;
    for(int i = 1;i <= (n<<1);++ i) fa[i] = i;
    for(int i = 1, v;i <= m;++ i){
        read(to[i]); read(v); read(val[i]);
        merge(rt[v], i);
    }
    for(int i = 1, j = 1, now;i <= n;j = ++i)
        while(!is[j]){
            while(!is[j]){
                is[j] = i; j = to[now = top(j)]; ans += val[now];
            } if(is[j] != i) break;
            while(is[j] == i){
                is[j] = -1; j = pre[j] = to[now = top(j)];
                pushtag(now, -val[now]);
            } ++ cnt;
            while(is[j] == -1){is[j] = i; comb(j, cnt); j = pre[j];} j = cnt;
        }
    printf("%d\n", ans);
}

CF671D Roads in Yusland

这是~~我目前仅知道的~~对偶线性规划模板~~(?)~~题。

线性规划对偶定理即当一对对偶线性规划同时有解时，它们的目标函数值相同 ( \(\min\{c^Tx|Ax\ge b,x\ge 0\}=\max\{b^Ty|A^Ty\le c,y\ge 0\}\)，其中\(b,c,x,y\) 为列向量，\(A\) 为矩阵 )

这个东西经常表明两个看上去完全不同的问题~~（而且一个是 \(\max\) 一个是 \(\min\)）~~，答案却是始终相同的。

题目描述：给定 \(n\) 个点的树和 \(m\) 条链 \((x,y)\)，保证以 \(1\) 为根时 \(x,y\) 为祖先-后代关系，每条链有权值。求选择一些链，使得每条边都被覆盖的权值和的最小值。

数据范围：\(n,m\le 3\times 10^5\)。

solution

设 \(c_i\) 为第 \(i\) 条链的权值，\(x_i\) 为第 \(i\) 条链是否选，\(A_{i,j}\) 为第 \(i\) 条边是否被第 \(j\) 条链覆盖，\(b_i\) 为全 \(1\) 向量，表示每条边都被覆盖。

首先要判无解，这个直接用树上差分就完事。

然后就可以套用线性规划对偶定理，问题转化为将每条边定一个非负权值，使得每条链上的边权和 \(\le\) 它的权值，且边权和最大。

这事一个经典贪心，显然从深向浅能放就放，用可并堆维护即可，时间复杂度 \(O(m\log m)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 300003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, cnt, head[N], to[N<<1], nxt[N<<1], dep[N], sum[N];
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
int rt[N], dis[N], fr[N], ch[N][2]; LL val[N], tag[N], ans;
void ptg(int x, LL v){tag[x] += v; val[x] += v;}
void psd(int x){
    if(tag[x]){
        int l = ch[x][0], r = ch[x][1];
        ptg(l, tag[x]); ptg(r, tag[x]); tag[x] = 0;
    }
}
void merge(int &x, int y){
    if(!x || !y){x += y; return;}
    if(val[x] > val[y]) swap(x, y); ptg(y, -tag[x]); merge(ch[x][1], y);
    if(dis[ch[x][0]] < dis[ch[x][1]]) swap(ch[x][0], ch[x][1]);
    dis[x] = dis[ch[x][1]] + 1;
}
void pop(int &x){psd(x); merge(ch[x][0], ch[x][1]); x = ch[x][0];}
void dfs(int x, int f = 0){
    dep[x] = dep[f] + 1;
    for(int i = head[x];i;i = nxt[i])
        if(to[i] != f){dfs(to[i], x); sum[x] += sum[to[i]]; merge(rt[x], rt[to[i]]);}
    if(!sum[x] && x > 1){puts("-1"); exit(0);}
    while(dep[fr[rt[x]]] >= dep[x]) pop(rt[x]);
    if(rt[x]){ans += val[rt[x]]; ptg(rt[x], -val[rt[x]]);}
}
int main(){
    read(n); read(m);
    for(int i = 1, x, y;i < n;++ i){
        read(x); read(y); add(x, y); add(y, x);
    }
    for(int i = 1, x, y;i <= m;++ i){
        read(x); read(y); read(val[i]);
        ++ sum[x]; -- sum[y]; fr[i] = y;
        merge(rt[x], i);
    } dfs(1); printf("%lld\n", ans);
}

然而有一个~~非常难受~~的易错点，就是线性规划里面的变量取实数值，在变量要求为整数时，若不能证明最优解必定在变量为整数时取得，则~~这东西废了~~。

去掉上面的 \((x,y)\) 祖先-后代关系的条件之后就是这种情况~~建议直接飞升~~

LOJ2842「JOISC 2018 Day 4」野猪

题目描述：给定 \(n\) 个点 \(m\) 条边的无向连通简单图，边带权，给定长为 \(l\) 的序列 \(\{x\}_{i=1}^l\)，求你从 \(x_1\) 出发，按顺序到达 \(x_2,\dots,x_l\)，且中途不走回头路的最短路长度，并支持 \(q\) 次 \(\{x\}\) 的单点修改。

数据范围：\(n,m\le 2000,l,q\le 10^5,\text{TL}=10\text s,\text{ML}=1\text{GiB}\)。

solution

两个点之间的路径只有以下 \(4\) 种情况：

最短路。
不经过 1. 的出发边的最短路
不经过 1. 的出发边和 2. 的到达边的最短路。
其余的最短路。

预处理即对于每条边跑一次 dijkstra，支持单点修改用线段树维护矩阵乘积即可。时间复杂度 \(O(m^3\log m+4^4q\log m)\)。

原来 == 的优先级比 ^ 要高，学到了...

还有初值不为 0 时要时刻记得赋初值...

#include <bits/stdc++.h>
#define MT make_tuple
using namespace std;
typedef long long LL;
typedef tuple<int, int, int> tii;
typedef tuple<LL, int, int> tli;
const int N = 2003, M = 100003;
const LL inf = 0x3f3f3f3f3f3f3f3fll;
template <typename T>
void read(T &x) {
    int ch = getchar();
    x = 0;
    for (; ch < '0' || ch > '9'; ch = getchar())
        ;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
}
template <typename T>
bool chmin(T &a, const T &b) {
    if (a > b)
        return a = b, 1;
    return 0;
}
int n, m, q, l, a[M], pre[4][N][N], nxt[4][N][N];
LL dis[N << 1][N << 1], f[4][N][N];
vector<tii> G[N];
tii used[N];
void dijkstra(int S, int nod, LL val, LL *dis) {
    memset(used, 0, sizeof used);
    memset(dis, 0x3f, N << 4);
    priority_queue<tli, vector<tli>, greater<tli> > pq;
    dis[S] = val;
    pq.push(MT(val, nod, S));
    while (!pq.empty()) {
        auto [_, u, eu] = pq.top();
        pq.pop();
        if (_ > dis[eu])
            continue;
        if (!get<1>(used[u])) {
            for (auto [v, w, ev] : G[u])
                if ((eu ^ ev) == 1)
                    used[u] = MT(v, w, ev);
                else if (chmin(dis[ev], dis[eu] + w))
                    pq.push(MT(dis[ev], v, ev));
        } else {
            auto [v, w, ev] = used[u];
            if (chmin(dis[ev], dis[eu] + w))
                pq.push(MT(dis[ev], v, ev));
        }
    }
}
struct Mat {
    LL v[4][4];
    int pre[4], nxt[4];
    Mat() { memset(v, 0x3f, sizeof v); }
    Mat(int a, int b) {
        memset(v, 0x3f, sizeof v);
        for (int i = 0; i < 4; ++i) {
            v[i][i] = f[i][a][b];
            pre[i] = ::pre[i][a][b];
            nxt[i] = ::nxt[i][a][b];
        }
    }
    Mat operator=(const Mat &o) {
        memcpy(v, o.v, sizeof v);
        memcpy(pre, o.pre, sizeof pre);
        memcpy(nxt, o.nxt, sizeof nxt);
        return *this;
    }
    Mat operator*(const Mat &o) const {
        Mat res;
        for (int i = 0; i < 4; ++i)
            for (int j = 0; j < 4; ++j)
                if (nxt[i] != o.pre[j])
                    for (int x = 0; x < 4; ++x)
                        for (int y = 0; y < 4; ++y) chmin(res.v[x][y], v[x][i] + o.v[j][y]);
        for (int i = 0; i < 4; ++i) {
            res.pre[i] = pre[i];
            res.nxt[i] = o.nxt[i];
        }
        return res;
    }
    LL val() {
        LL res = inf;
        for (int i = 0; i < 4; ++i)
            for (int j = 0; j < 4; ++j) chmin(res, v[i][j]);
        return res == inf ? -1 : res;
    }
} seg[M << 2];
void build(int x = 1, int L = 1, int R = l - 1) {
    if (L == R) {
        seg[x] = Mat(a[L], a[L + 1]);
        return;
    }
    int mid = L + R >> 1;
    build(x << 1, L, mid);
    build(x << 1 | 1, mid + 1, R);
    seg[x] = seg[x << 1] * seg[x << 1 | 1];
}
void upd(int p, int x = 1, int L = 1, int R = l - 1) {
    if (L == R) {
        seg[x] = Mat(a[L], a[L + 1]);
        return;
    }
    int mid = L + R >> 1;
    if (p <= mid)
        upd(p, x << 1, L, mid);
    else
        upd(p, x << 1 | 1, mid + 1, R);
    seg[x] = seg[x << 1] * seg[x << 1 | 1];
}
int main() {
    read(n);
    read(m);
    read(q);
    read(l);
    for (int i = 0, a, b, c; i < m; ++i) {
        read(a);
        read(b);
        read(c);
        G[a].emplace_back(b, c, i << 1);
        G[b].emplace_back(a, c, i << 1 | 1);
    }
    memset(f, 0x3f, sizeof f);
    for (int u = 1; u <= n; ++u)
        for (auto [v, w, id] : G[u]) dijkstra(id, v, w, dis[id]);
    for (int i = 1; i <= l; ++i) read(a[i]);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j)
                for (auto [u, _, eu] : G[i])
                    for (auto [v, __, ev] : G[j])
                        if (chmin(f[0][i][j], dis[eu][ev ^ 1])) {
                            pre[0][i][j] = u;
                            nxt[0][i][j] = v;
                        }
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j)
                for (auto [u, _, eu] : G[i])
                    if (u != pre[0][i][j])
                        for (auto [v, __, ev] : G[j])
                            if (chmin(f[1][i][j], dis[eu][ev ^ 1])) {
                                pre[1][i][j] = u;
                                nxt[1][i][j] = v;
                            }
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j)
                for (auto [u, _, eu] : G[i])
                    if (u != pre[0][i][j])
                        for (auto [v, __, ev] : G[j])
                            if (v != nxt[1][i][j] && chmin(f[2][i][j], dis[eu][ev ^ 1])) {
                                pre[2][i][j] = u;
                                nxt[2][i][j] = v;
                            }
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            if (i != j)
                for (auto [u, _, eu] : G[i])
                    if ((nxt[0][i][j] != nxt[1][i][j] || pre[2][i][j] != u) &&
                        (nxt[0][i][j] == nxt[1][i][j] || pre[1][i][j] != u))
                        for (auto [v, __, ev] : G[j])
                            if (v != nxt[0][i][j] && chmin(f[3][i][j], dis[eu][ev ^ 1])) {
                                pre[3][i][j] = u;
                                nxt[3][i][j] = v;
                            }
    build();
    while (q--) {
        int p;
        read(p);
        read(a[p]);
        if (p < l)
            upd(p);
        if (p > 1)
            upd(p - 1);
        printf("%lld\n", seg[1].val());
    }
}

LOJ2836「JOISC 2018 Day 2」最差记者 3

solution

设 \(b_i\) 表示 \(i\) 一次走几步，显然它是个定值，且 \(b_i=b_{i-1}\lceil\frac{a_i}{b_{i-1}}\rceil\)，所以 \(b\) 单调递增且只有 \(O(\log V)\) 个值，相同 \(b\) 的部分一起移动，直接分别处理每一段即可，时间复杂度 \(O(n\log V)\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 31;
template <typename T>
void read(T &x) {
    int ch = getchar();
    x = 0;
    for (; ch < '0' || ch > '9'; ch = getchar())
        ;
    for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
}
int n, q, m, c[N], l[N], r[N];
int main() {
    read(n);
    read(q);
    int nowl = 0, nowr = 0, now = 1;
    for (int i = 1, d; i <= n; ++i) {
        read(d);
        if (d <= now)
            nowr = i;
        else {
            c[m] = now;
            l[m] = nowl;
            r[m++] = nowr;
            now = (now + d - 1) / now * now;
            nowl = nowr = i;
        }
    }
    c[m] = now;
    l[m] = nowl;
    r[m++] = nowr;
    while (q--) {
        int x, L, R, ans = 0;
        read(x);
        read(L);
        read(R);
        for (int i = 0; i < m; ++i) {
            int t = x / c[i] * c[i];
            ans += max(0, min(R, t - l[i]) - max(L, t - r[i]) + 1);
        }
        printf("%d\n", ans);
    }
}

CF1163F Indecisive Taxi Fee

题目描述：给定 \(n\) 个点 \(m\) 条边的无向图，边带权，\(q\) 次询问一条边，求不能经过它的 \(1\) 到 \(n\) 的最短路。

数据范围：\(n,m,q\le 2\times 10^5\)。

solution

只用考虑它在最短路上时的情形。

随便跑一条 \(1\) 到 \(n\) 的最短路，然后预处理从 \(1\) 和 \(n\) 出发的最短路长度。

对于一个最短路之外的点 \(u\)，\(1\) 到 \(u\) 的最短路与 \(1\) 到 \(n\) 的最短路重合一段前缀，设 \(L(u)\) 为这段前缀的位置。\(R(u)\) 同理。

对于一条最短路之外的边 \((u,v)\)，经过它的最短路为 \(1\rightarrow u\rightarrow v\rightarrow n\) 和 \(1\rightarrow v\rightarrow u\rightarrow n\)，两种情况同理，考虑第一种，即为若断掉的是 \((L(u),R(v)]\) 上的边，那么 \((u,v)\) 就可能成为最短路上的边，用它来更新这一段的答案。

用线段树维护即可，时间复杂度 \(O(m\log m+q)\)。

LOJ2835「JOISC 2018 Day 2」路网服务

solution

注意到这些新加的边共用一个点是非常优的。

直接上模拟退火，每次暴力单点修改并扔进 \(O(n^2)\) spj，所有点跑 1h 左右就能拿到 91 分的好成绩~~Task 1 几乎秒出~~。

好心人会把答案放在这里让大家抄题解

#include<bits/stdc++.h>
using namespace std;
const int N = 1003;
const double delta = 0.9975;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
int n, k, w0, cnt, a[N], b[N], f[N], res[N], head[N], to[N*3], nxt[N*3], dep[N], q[N], fr, re, ans, rans = 1e9;
void add(int u, int v){
    to[++cnt] = v; nxt[cnt] = head[u]; head[u] = cnt;
    to[++cnt] = u; nxt[cnt] = head[v]; head[v] = cnt;
}
int calc(){
    int res = 0;
    for(int S = 0;S < n-1;++ S){ cnt = fr = re = 0;
        memset(head, 0, sizeof head); memset(dep, 0x3f, sizeof dep);
        for(int i = 0;i < n-1;++ i) add(a[i], b[i]);
        for(int i = 0;i < k;++ i) add(f[k], f[i]);
        q[re++] = S; dep[S] = 0;
        while(fr < re){
            int u = q[fr++];
            for(int i = head[u];i;i = nxt[i])
                if(chmin(dep[to[i]], dep[u] + 1))
                    q[re++] = to[i];
        }
        for(int i = S+1;i < n;++ i) res += dep[i];
    } return res;
}
int main(){
    read(n); read(k); read(w0); cerr << n << " " << k << " " << w0 << endl;
    for(int i = 0;i < n-1;++ i){read(a[i]); read(b[i]); -- a[i]; -- b[i];}
    for(int i = 0;i <= k;++ i) f[i] = rng() % n; 
    for(int _ = 0;_ < 6;++ _){
        double T = 1e4;
        if(chmin(rans, ans = calc())){memcpy(res, f, sizeof f); cerr << ans << endl;}
        while(T > 1e-14){
            int p = rng() % (k+1), tmp = f[p]; f[p] = rng() % n;
            int dans = calc() - ans;
            if(dans < 0){ans += dans; if(chmin(rans, ans)){memcpy(res, f, sizeof f); cerr << ans << endl;}}
            else if(exp(-dans / T) * UINT_MAX < rng()) f[p] = tmp;
            T *= delta;
        }
    } printf("%d\n", rans);
    for(int i = 0;i < k;++ i) printf("%d %d\n", res[k] + 1, res[i] + 1);
}

CODE FESTIVAL 2017 qual C

F Three Gluttons

solution

考虑什么时候方案合法：

小 A 和小 B 不会选到同一个数。
对于一个数 \(x\)，小 A 和小 B 经过 \(x\) 时都没有选它，则在之前要被小 C 选过

发现答案是两部分的乘法原理：合法选位置的个数 \(\times\) 填数的方案。

后者可以 dp 解决，设 \(dp_{i,j}\) 表示考虑到第 \(i\) 个，当前剩下 \(j\) 个数可以填。

AGC010

D Decrementing

题目描述：有 \(n\) 堆石子，一开始第 \(i\) 堆石子有 \(a_i\) 个。两人轮流操作，每次从一个石子数 \(>1\) 的石子堆取走一个石子，然后将所有堆的石子数除以它们的 \(\gcd\)。无法操作的人输，求两人绝对聪明时，先手必胜还是后手必胜。

数据范围：\(n\le 10^5,a_i\le 10^9,\gcd\{a\}=1\)。

solution

若不考虑除法操作，答案就取决于 \(sum-n\) 的奇偶性。

由于 \(\gcd\) 为 \(1\)，则必定存在一个奇数。

若偶数有奇数个，则先手可以将局面变为至少两个奇数，且偶数有偶数个，不管后手如何操作，先手总可以维持至少有一个奇数，则整体的奇偶性可以永不改变，而此时 \(sum-n\) 永远是奇数，所以先手必胜。
若偶数有偶数个，根据上述讨论，奇数有至少两个时为后手必胜，奇数只有一个时，若先手对偶数进行操作则后手胜利，所以先手应该对唯一的奇数操作，然后递归处理。

时间复杂度 \(O(n\log n\log V)\)。

#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int gcd(int a, int b){return b ? gcd(b, a % b) : a;}
int n, a[N], cnt[2]; bool fl, ans;
int main(){
    read(n);
    for(int i = 1;i <= n;++ i) read(a[i]);
    while(true){
        cnt[0] = cnt[1] = 0; fl = false;
        for(int i = 1;i <= n;++ i){++ cnt[a[i] & 1]; fl |= a[i] == 1;}
        if(cnt[0] & 1){ans ^= 1; break;}
        if(cnt[1] > 1 || fl) break;
        int g = a[1] - (a[1] & 1);
        for(int i = 2;i <= n;++ i) g = gcd(g, a[i] - (a[i] & 1));
        for(int i = 1;i <= n;++ i) a[i] /= g; ans ^= 1;
    } puts(ans ? "First" : "Second");
}

E Rearranging

题目描述：给定长为 \(n\) 的正整数序列 \(a\)，两人依次操作，先手任意打乱顺序，后手可以做任意次操作：选择两个互质的数并交换。先手想让字典序尽可能小，后手想让字典序尽可能大，求两人绝对聪明时，最后的序列。

数据范围：\(n\le 2000,a_i\le 10^8\)。

solution

后手能从序列 \(a\) 操作到序列 \(a'\) 的充要条件就是：\(\forall\gcd(a_i,a_j)>1,a_i\) 和 \(a_j\) 的相对顺序没有改变。
必要性显然，充分性~~感性理解(?)~~也很显然(?)
问题转化为对于无向图 \((V,E)\) 其中 \(V=[n],E=\{(u,v)|\gcd(a_u,a_v)>1\}\)，先手给每条边定向使得它是个 DAG，后手求最大拓扑序。
显然方向从小到大是最优的，直接求拓扑序即可，时间复杂度 \(O(n^2\log V)\)。

#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 2003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int gcd(int a, int b){return b ? gcd(b, a % b) : a;}
int n, a[N], deg[N]; bool vis[N]; vector<int> E[N]; priority_queue<pii> pq;
void dfs(int u){
    vis[u] = true;
    for(int v = 1;v <= n;++ v)
        if(!vis[v] && gcd(a[u], a[v]) > 1){
            E[u].push_back(v); ++ deg[v]; dfs(v);
        }
}
int main(){
    read(n);
    for(int i = 1;i <= n;++ i) read(a[i]);
    sort(a + 1, a + n + 1);
    for(int i = 1;i <= n;++ i) if(!vis[i]) dfs(i);
    for(int i = 1;i <= n;++ i) if(!deg[i]) pq.push(MP(a[i], i));
    while(!pq.empty()){
        printf("%d ", pq.top().fi); int u = pq.top().se; pq.pop();
        for(int v : E[u]) if(!--deg[v]) pq.push(MP(a[v], v));
    }
}

F Tree Game

题目描述：给定 \(n\) 个点的树，每个点上面有 \(a_i\) 个石子，求对于所有 \(v\in[1,n]\cap\Z\)，若一开始有一个棋子在结点 \(v\)，两人轮流操作，每次在棋子所在结点取走 \(1\) 个石子，然后移动到相邻位置，使得两人绝对聪明时，先手必胜。

数据范围：\(n\le 3000,a_i\le 10^9\)。

solution

取一个点 \(r\) 作为根，设 \(f(x)\) 表示从 \(x\) 开始，只考虑 \(x\) 的子树时，先手是否必胜。则 \(f(x)=1\Leftrightarrow \exist v\in\text{son}(u),f(v)=0,a_v<a_x\)。则 \(f(r)\) 即为从 \(r\) 开始时先手是否必胜。

#include<bits/stdc++.h>
#define PB push_back
using namespace std;
const int N = 3003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, a[N]; vector<int> E[N];
bool dfs(int x, int f = 0){
    bool res = false;
    for(int v : E[x]) if(v != f && a[v] < a[x] && !dfs(v)){res = true; break;}
    return res;
}
int main(){
    read(n);
    for(int i = 1;i <= n;++ i) read(a[i]);
    for(int i = 1, u, v;i < n;++ i){read(u); read(v); E[u].PB(v); E[v].PB(u);}
    for(int i = 1;i <= n;++ i) if(dfs(i)) printf("%d ", i);
}

AGC011

C Squared Graph

题目描述：给定无向图 \(G=(V,E)\)，定义 \(G^2=(V^2,E')\)，其中 \(E'=\{((a,b),(c,d))\big|(a,c)\in E,(b,d)\in E\}\)，求 \(G^2\) 的连通块数。

数据范围：\(n\le 10^5,m\le 2\times 10^5\)。

solution

首先去掉孤立点（设有 \(x\) 个），这些点贡献 \(n^2-(n-x)^2\) 个连通块。

然后对于 \(G\) 中的两个连通块，二分图 \(\times\) 二分图贡献 \(2\) 个连通块，其他情况贡献 \(1\) 个连通块。

直接计数即可，复杂度 \(O(n+m)\)。

D Half Reflector

题目描述：你有 \(n\) 个 sd 排成一排，每个 sd 有 AB 两种状态。给定正整数 \(n,k\) 和每个 sd 的初始状态，一次操作从左边扔给第 \(1\) 个 sd 一只球，求 \(k\) 次操作之后 sd 们的状态。一只 sd 从左(右)边接到球之后，若它是 A 状态，则会扔回左(右)边然后变为 B 状态；若它是 B 状态，则会扔到右(左)边然后变为 A 状态。

数据范围：\(n\le 2\times 10^5,k\le 10^9\)。

solution

设 \(s_i\) 表示第 \(i\) 个 sd 的状态。若 \(s_1=\) A，则 \(s_1\) 变为 B。若 \(s_1=\) B，则显然最终球从右边出去，因为每次球到达第 \(1\) 个 sd 时都会向右。

若某个时刻球从左边到达了第 \(i\) 个 sd，则 \(s_{i-1}=\) A（从 B 取反得到的）

若 \(s_i=\) A，则会被扔回来，球越过第 \(i\) 个 sd，状态变为 \(s_{i-1}=\) B。
若 \(s_i=\) B，则会被扔过去，球越过第 \(i\) 个 sd，状态变为 \(s_{i-1}=\) A。

并且最终 \(s_n=\) A。这告诉我们一次操作就是向左循环移位并取反。于是就可以做到 \(O(1)\) 一次操作。

若最后有一堆 BABABA，这个结构不会被破坏，每至多 \(2\) 次操作还会变长，于是若 \(k>2n\) 则答案必定为 BA...BA（\(n\) 为偶数）或 ?BA...BA（\(n\) 为奇数，此时 \(s_1\) 在交替变化）。于是就可以直接模拟，时间复杂度 \(O(n)\)。

#include<cstdio>
using namespace std;
const int N = 200003;
int n, k, l; bool rev, a[N]; char str[N];
int main(){
    scanf("%d%d%s", &n, &k, str);
    for(int i = 0;i < n;++ i) a[i] = str[i] == 'B';
    if(k > (n<<1)+1) k = (n<<1) + 1 + !(k - (n<<1) & 1);
    while(k --){if(a[l] == rev) a[l] ^= 1;else {++ l; if(l == n) l = 0; rev ^= 1;}}
    for(int i = l;i < n;++ i) putchar((a[i]^rev) + 'A');
    for(int i = 0;i < l;++ i) putchar((a[i]^rev) + 'A');
}

E Increasing Numbers

题目描述：定义飞升数是 \(10\) 进制下数位从高到低不降的数。给定正整数 \(n\)，求最小的正整数 \(k\)，使得存在 \(k\) 个飞升数的和是 \(n\)。

数据范围：\(n\le 10^{5\cdot10^5}\)。

solution

不容易发现，飞升数等价于 \(9\) 个形如 \(11\dots11\) 的数的和。

然后就容易发现，答案 \(\le k\) 等价于 \(9(n+k)\) 的数字和 \(\le 9k\)。

直接模拟，时间复杂度 \(O(n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 500003;
char str[N]; int a[N], dsum;
int main(){
    scanf("%s", str); a[0] = strlen(str);
    for(int i = 1;i <= a[0];++ i) a[i] = str[a[0] - i] - '0'; ++ a[0];
    for(int i = 1, x = 0;i <= a[0];++ i){a[i] = 9 * a[i] + x; x = a[i] / 10; a[i] %= 10;}
    while(a[0] && !a[a[0]]) -- a[0];
    for(int i = 1;i <= a[0];++ i) dsum += a[i];
    for(int k = 1;;++ k){
        a[1] += 9; dsum += 9;
        for(int i = 1;a[i] > 9;++ i){a[i] -= 10; ++ a[i+1]; dsum -= 9;}
        if(a[a[0] + 1]) ++ a[0];
        if(dsum <= k * 9){printf("%d\n", k); return 0;}
    }
}

AGC012

C Tautonym Puzzle

题目描述：给定正整数 \(n\)，构造字符串 \(S\) 使得

\(|\Sigma|=100\)。
\(|S|\le 200\)。
\(S\) 有 \(n\) 个非空子序列是平方串。

数据范围：\(n\le 10^{12}\)。

solution

每次插两个相同字符，插在末尾和开头答案+1，插在末尾和中间答案*2。

```cpp #include using namespace std; typedef long long LL; const int N = 103; LL n; int a[N], b[N], c, d; void solve(LL n){ if(n == 1) return; solve(n>>1); ++d; b[d] = c+d; if(n & 1){++ c; a[c] = c+d;} } int main(){ scanf("%lld", &n); solve(n + 1); printf("%d\n", c+d<<1); for(int i = c;i;-- i) printf("%d ", a[i]); for(int i = 1;i <= d;++ i) printf("%d ", b[i]); for(int i = 1;i <= c+d;++ i) printf("%d ", i); } ```

D Colorful Balls

题目描述：给定一排 \(n\) 个球和正整数 \(X,Y\)，第 \(i\) 个球的颜色是 \(c_i\)，权值是 \(w_i\)。可以做任意次以下两种操作：

交换两个颜色相同且权值和 \(\le X\) 的球的位置。
交换两个颜色不同且权值和 \(\le Y\) 的球的位置。

求能得到的球的颜色的序列数量\(\bmod(10^9+7)\)。

数据范围：\(1\le c_i\le n\le 2\times 10^5,1\le w_i,X,Y\le 10^9\)。

solution

对于每种颜色 \(c\)，设 \(v_c\) 表示颜色为 \(c\) 的球中权值最小值。则当 \(w_i\le X-v_c\) 时令 \(w_i:=v_c\)。

现在只考虑第二种操作，每次交换使用全局最小值或次小值（当与最小值颜色相同时）作为中转站是最优的，这个操作具有传递性。因此得到的这些序列就是其中一个子集可以随意排列，剩下的部分无法动弹，容易计算方案数。

时间复杂度 \(O(n)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200003, mod = 1e9 + 7;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, A, B, c[N], w[N], ans[N], inv[N], mc[N], mn, mx, sum, res = 1;
int ksm(int a, int b){
    int res = 1;
    for(;b;b >>= 1, a = (LL) a * a % mod)
        if(b & 1) res = (LL) res * a % mod;
    return res;
}
int main(){
    read(n); read(A); read(B); memset(mc, 0x3f, sizeof mc);
    for(int i = 1;i <= n;++ i){read(c[i]); read(w[i]); chmin(mc[c[i]], w[i]);}
    for(int i = 1;i <= n;++ i) if(w[i] + mc[c[i]] <= A) w[i] = mc[c[i]];
    for(int i = 1;i <= n;++ i)
        if(mc[mn] >= mc[i]){mx = mn; mn = i;}
        else if(mc[mx] > mc[i]) mx = i;
    for(int i = 1;i <= n;++ i)
        if(c[i] != mn && w[i] + mc[mn] <= B || w[i] + mc[mx] <= B){
            ++ ans[c[i]]; ++ sum;
        }
    for(int i = 1;i <= sum;++ i) res = (LL) res * i % mod;
    inv[sum] = ksm(res, mod-2);
    for(int i = sum;i;-- i) inv[i-1] = (LL) inv[i] * i % mod;
    for(int i = 1;i <= n;++ i) res = (LL) res * inv[ans[i]] % mod;
    printf("%d\n", res);
}

E Camel and Oases

题目描述：给定一维沙漠中 \(n\) 个绿洲，第 \(i\) 个绿洲在 \(x_i\) 位置，你初始有一只驼峰大小为 \(V\) 的骆驼，可以储存 \(V\) 单位体积的水。你可以做以下两种操作：

走 \(1\) 单位长度，消耗 \(1\) 单位体积的水。
若你当前在绿洲，则可以将驼峰装满。
瞬移到一个绿洲，将 \(V\) 变为 \(\lfloor\frac V2\rfloor\)。

对于每个绿洲，求你是否有可能从这个绿洲开始，到达过每个绿洲至少一次。

数据范围：\(n,V\le 2\times 10^5,x_i<x_{i+1},|x_i|\le 10^9\)。

solution

发现至多瞬移 \(18\) 次，相当于有 \(19\) 个区间序列，在每个序列中选一个使得并为全集。

枚举第一列的区间。从这个区间开始，若能到达所有绿洲，则这个区间的绿洲均 OK。

现在判断其他 \(18\) 个能否覆盖一段前缀和一段后缀，直接状压 dp 即可。

以前缀为例，设 \(f_S\) 表示取了 \(S\) 这些序列，最远能覆盖到哪里，转移枚举还未选的一列，二分出最近的有用的一个区间。

时间复杂度 \(O(n+2^{18}\log n)\)。

#include<bits/stdc++.h>
#define PB emplace_back
using namespace std;
const int N = 200003, M = 1<<19;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0; bool f = false;
    for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
    if(f) x = -x;
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, m, lim, V, x[N], d[N], f[M], g[M]; vector<int> seg[20];
int main(){
    read(n); read(V); m = 32 - __builtin_clz(V); lim = 1<<m;
    for(int i = 1;i <= n;++ i) read(x[i]);
    for(int i = 1;i < n;++ i) d[i] = x[i+1] - x[i]; d[0] = d[n] = 1e9;
    for(int i = 0;i <= m;++ i)
        for(int j = 0;j <= n;++ j)
            if(d[j] > (V>>i)) seg[i].PB(j);
    if(seg[0].size() > m+2){
        for(int i = 1;i <= n;++ i) puts("Impossible");
        return 0;
    } for(int i = 0;i < lim;++ i){f[i] = 0; g[i] = n;}
    for(int S = 0;S < lim;++ S)
        for(int i = 0;i < m;++ i) if(!(S >> i & 1)){
            chmax(f[S|1<<i], *upper_bound(seg[i+1].begin(), seg[i+1].end(), f[S]));
            chmin(g[S|1<<i], *(lower_bound(seg[i+1].begin(), seg[i+1].end(), g[S])-1));
        }
    for(int i = 1;i < seg[0].size();++ i){
        int L = seg[0][i-1], R = seg[0][i]; bool flg = false;
        for(int S = 0;S < lim && !flg;++ S)
            flg |= f[S] >= L && g[lim-1-S] <= R;
        for(int j = L+1;j <= R;++ j) puts(flg ? "Possible" : "Impossible");
    }
}

AGC013

D Pilling Up

题目描述：给定正整数 \(n,m\)，每个 sd 有黑白两种颜色，初始有 \(n\) 个 sd，但不知道它们的颜色，每次操作取出一个 sd，放入黑白各一个 sd，再取出一个 sd。求做 \(m\) 次操作之后，可能得到的颜色序列数量\(\bmod(10^9+7)\)。

数据范围：\(n,m\le 3000\)。

solution

设 \(f_{i,j}\) 表示做 \(i\) 次操作，剩余 \(j\) 个黑球的方案数。则 \(f_{i,j}=f_{i-1,j-1}+2f_{i-1,j}+f_{i-1,j+1}\)，这是一个格路计数问题，但是它会算重。

发现只需要减去 \(n-1,m\) 的答案，使得其必定经过 \(j=0\) 即可，时间复杂度 \(O(nm)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3003, mod = 1e9 + 7;
int n, m; unsigned f[2][N];
void qmo(int &x){x += x >> 31 & mod;}
int calc(int m, int n){
    int ans = 0, cur = 0;
    for(int i = 1;i <= m;++ i) f[0][i] = 1;
    f[0][0] = f[0][m+1] = f[1][0] = f[1][m+1] = 0;
    for(int i = 0;i < n;++ i, cur ^= 1)
        for(int j = 1;j <= m;++ j)
            f[!cur][j] = (f[cur][j-1] + f[cur][j] * 2 + f[cur][j+1]) % mod;
    for(int i = 1;i <= m;++ i) qmo(ans += f[cur][i] - mod);
    return ans;
}
int main(){
    scanf("%d%d", &n, &m);
    printf("%lld\n", 4ll * (calc(n, m-1) - calc(n-1, m-1) + mod) % mod);
}

E Placing Squares

题目描述：给定大小为 \(m\) 的正整数集 \(X\)，对于所有和为 \(n\) 的正整数序列 \(a\)，若它的所有前缀和都 \(\notin X\)，则它的贡献为 \(\prod\limits_{i=1}^na_i^2\)，求所有正整数序列的贡献之和\(\bmod (10^9+7)\)。

数据范围：\(n\le 10^9,m\le 10^5,X_1<\dots<X_m<n\)。

solution

对于这个贡献值，可以转化一下。在 \(n\) 个位置上，可以放一个绿球、一个红球或都有，并在一些分隔的位置放上隔板，开头和末尾必须有隔板，钦定一些位置不能放隔板，并且两个隔板之间恰好有一个红球和一个绿球。

这个就可以直接 dp 了，设 \(dp_{i,0/1/2}\) 表示在 \(i\) 个位置上，从上一个隔板到现在放了多少个球。能放隔板的转移用矩阵快速幂，不能放的只有 \(m\) 个位置，可以暴力。时间复杂度 \(O((3^3+3^2m)\log n)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7, E[3][3] = {
    {2, 1, 1}, {2, 1, 0}, {1, 1, 1}
}, F[3][3] = {
    {1, 0, 0}, {2, 1, 0}, {1, 1, 1}
};
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, x[N];
struct Mat {
    int n, m, x[3][3];
    Mat(int _n = 3, int _m = 3): n(_n), m(_m){memset(x, 0, sizeof x);}
    Mat operator = (const Mat &o){n = o.n; m = o.m; memcpy(x, o.x, sizeof x); return *this;}
    Mat operator = (const int v[3][3]){memcpy(x, v, sizeof x); return *this;}
    Mat operator * (const Mat &o) const {
        Mat res(n, o.m);
        for(int i = 0;i < n;++ i)
            for(int k = 0;k < m;++ k)
                for(int j = 0;j < o.m;++ j)
                    res.x[i][j] = (res.x[i][j] + (LL) x[i][k] * o.x[k][j]) % mod;
        return res;
    }
} ans(3, 1), pw[31], G;
void calc(int k){for(int i = 0;i < 31;++ i) if(k >> i & 1) ans = pw[i] * ans;}
int main(){
    read(n); read(m); ans.x[0][0] = 1;
    for(int i = 1;i <= m;++ i) read(x[i]);
    sort(x + 1, x + m + 1); pw[0] = E; G = F;
    for(int i = 1;i < 31;++ i) pw[i] = pw[i-1] * pw[i-1];
    for(int i = 1;i <= m;++ i){calc(x[i] - x[i-1] - 1); ans = G * ans;}
    calc(n - x[m]); printf("%d\n", ans.x[2][0]); 
}

AGC015

D A or...or B Problem

题目描述：给定正整数 \(a,b\)，求

\[\left|\{\text{OR}_{x\in S}x | \varnothing\ne S\subseteq[a,b]\}\right| \]

数据范围：\(a\le b<2^{60}\)。

solution

先特判 \(a=b\)。容易发现去掉 \(a,b\) 的 lcp 后答案不变。

此时必定存在 \(k\) 使得 \(a<2^k\le b\)。现在我们将区间分为两部分：\([a,2^k)\) 和 \([2^k,b]\)。

前一种可以搞出来 \([a,2^k)\)，后一种可以搞出来 \([2^k,2^k+2^{t+1}-1]\)，其中 \(t=b-2^k\) 的最高位。

两种一起可以搞出来 \([2^k+a,2^{k+1}-1]\)。将这三个区间取并即可。

#include<cstdio>
using namespace std;
typedef long long LL;
LL a, b, k;
void upb(LL &x){while(x != (x & -x)) x -= x & -x;}
int main(){
	freopen("a.in", "r", stdin);
	freopen("a.out", "w", stdout);
	scanf("%lld%lld", &a, &b);
	if(a == b){puts("1"); return 0;}
	k = a ^ b; upb(k);
	a &= k-1; b &= k-1; upb(b);
	if(b) b = (b<<1)-1;
	printf("%lld\n", (k<<1)-a - (b<a?a-1-b:0));
}

AGC016

E Poor Turkeys

题目描述：给定 \(n\) 盏灯，一开始是全亮的，有 \(m\) 个操作 \((x,y)\)，表示若 \(x,y\) 中至少一个亮，则随机选一个亮的关掉。求有多少个整数对 \((i,j)\) （\(1\le i<j\le n\)）满足 \(i,j\) 有可能同时亮。

数据范围：\(n\le 400,m\le 10^5\)。

从后往前考虑，如果 \(i\) 可以亮，则必须有一些灯可以亮。对于一组操作 \((x,y)\)，如果 \(i\) 同时需要 \(x,y\) 亮才能亮，那么 \(i\) 必关，否则若 \(i\) 只需要 \(x\) 亮，则 \(y\) 也要亮，另一种情况同理。

如果 \(i,j\) 都可以亮，那么它们可以同时亮当且仅当它们不同时需要另外一个灯亮。因为 \(i\) 需要 \(x\) 亮等价于 \(x\) 需要被关掉让 \(i\) 亮，而一个灯不能被关两次。

使用 bitset 判断，时间复杂度 \(O(nm+\frac{n^3}w)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 403, M = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, a[M], b[M], ans; bitset<N> S[N]; bool ok[N];
int main(){
    read(n); read(m);
    for(int i = 1;i <= m;++ i){read(a[i]); read(b[i]);}
    for(int i = 1;i <= n;++ i){
        S[i][i] = 1;
        for(int j = m;j;-- j){
            bool x = S[i][a[j]], y = S[i][b[j]];
            if(x && y){ok[i] = true; break;}
            else if(x) S[i][b[j]] = true;
            else if(y) S[i][a[j]] = true;
        }
    }
    for(int i = 1;i <= n;++ i) if(!ok[i])
        for(int j = i+1;j <= n;++ j)
            ans += !(ok[j] || (S[i] & S[j]).count());
    printf("%d\n", ans);
}

F Games on DAG

题目描述：给定 \(n\) 个点 \(m\) 条边的 DAG，求有多少边集使得 \(SG(1)=SG(2)\)。

数据范围：\(2\le n\le 15\)，无重边，点的标号是拓扑序。

solution

经典的状压 dp，设 \(f_S\) 表示点集 \(S\) 内的答案。枚举 \(S\) 中 SG 值为 \(0\) 的点集 \(T\)。设 \(T'=S-T\)，转移考虑如何连边：

\(T\) 内部不能连边。
\(T\) 向 \(T'\) 随便连边。
\(T'\) 中每个点必须向 \(T\) 中至少一个点连边。
\(T'\) 内部连边方案数是 \(f_{T'}\)。

这河狸么？这恒河里()因为 DAG 中去掉所有 SG 值为 \(0\) 的点后，其他点的 SG 值全部减 \(1\)，这是一个子问题。

这也能得到 \(f_S\) 中的 \(S\) 必须保证 \([1\in S]=[2\in S]\)。

时间复杂度 \(O(n3^n)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 15, M = 1<<N, mod = 1e9 + 7;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
void qmo(int &x){x += x >> 31 & mod;}
int n, m, lim, E[N], siz[M], f[M], ans = 1;
int main(){
    read(n); read(m); lim = 1<<n;
    for(int i = 0, u, v;i < m;++ i){
        read(u); read(v); -- u; -- v;
        E[u] |= 1<<v; qmo(ans += ans - mod);
    } f[0] = 1;
    for(int i = 1;i < lim;++ i) siz[i] = siz[i>>1] + (i&1);
    for(int S = 3;S < lim;++ S) if((S & 1) == (S >> 1 & 1))
        for(int T = S;T;T = (T - 1) & S) if((T & 1) == (T >> 1 & 1)){
            int tmp = 1, U = S ^ T;
            for(int i = 0;i < n;++ i) if(S >> i & 1)
                if(T >> i & 1) tmp = tmp * (1ll << siz[E[i] & U]) % mod;
                else tmp = tmp * ((1ll << siz[E[i] & T]) - 1) % mod;
            f[S] = (f[S] + (LL) tmp * f[U]) % mod;
        }
    qmo(ans -= f[lim-1]); printf("%d\n", ans);
}

AGC017

C Snuke and Spells

经典题出处，数 \(i\) 定义区间 \([i-cnt_i,i)\)，则答案是 \([0,n)\) 中没有被覆盖的长度。可以 \(O(n+q)\) 维护。

D Game on Tree

容易发现 \(SG(u)=\bigoplus_{v\in\text{son}(u)}(SG(v)+1)\)，因为 \(v\) 子树内既可以删子树内的边，也可以直接砍掉 \((u,v)\) 到达状态 \(0\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 100003;
int n, cnt, head[N], to[N<<1], nxt[N<<1], dp[N];
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
void dfs(int x, int f = 0){
    for(int i = head[x];i;i = nxt[i])
        if(to[i] != f){dfs(to[i], x); dp[x] ^= dp[to[i]] + 1;}
}
int main(){
    scanf("%d", &n);
    for(int i = 1, u, v;i < n;++ i){
        scanf("%d%d", &u, &v);
        add(u, v); add(v, u);
    } dfs(1); puts(dp[1] ? "Alice" : "Bob");
}

E Jigsaw

奇妙的图论转化。

solution

发现若 \(c_i\ne 0\) 时 \(a_i\) 无意义，左矩形必定是被垫起来的，右矩形同理。

容易发现，每个图形有意义的就是左右的上下边界，具体来说是这样的。

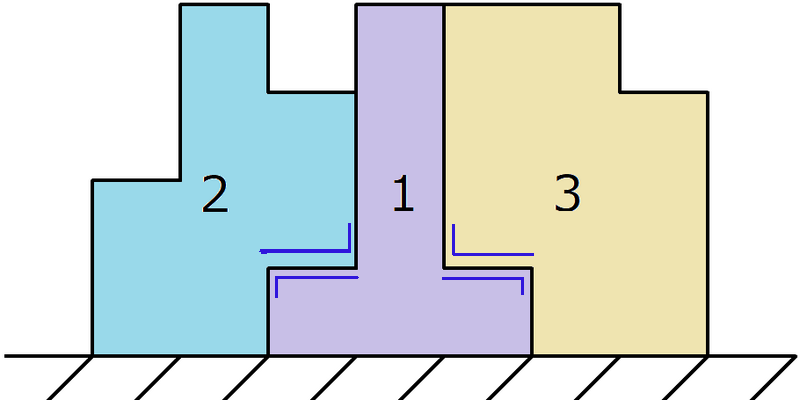
你只需要关心的是同一高度上这两种边界的匹配。对于每一个高度 \(x\)，建两个点，称 | 在左边的边界为正点，在右边的叫负点，每个图形看作一条边，且所有边都从正点连向负点。

那么合法的一堆图形就是一条路径。再建一个超级源，连向开头，被结尾连，形成回路，要求每条边经过恰好一次，即对于每个弱连通块求欧拉回路。

然后就可以得到，方案存在的充要条件是：

所有正点的入度 \(\le\) 出度，所有负点的入度 \(\ge\) 出度。只有这样才能用超级源补度数使得每个点的入度 \(=\) 出度。
每个弱连通块至少存在一个点入度 \(\ne\) 出度，否则超级源就进不去了。

直接判断即可，时间复杂度 \(O(n)\)。

#include<bits/stdc++.h>
#define PB push_back
using namespace std;
const int N = 403;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, h, deg[N]; bool vis[N], flg;
vector<int> E[N];
void dfs(int u){
    vis[u] = true; flg |= deg[u];
    for(int v : E[u]) if(!vis[v]) dfs(v);
}
int main(){
    read(n); read(h);
    while(n --){
        int a, b, c, d; read(a); read(b); read(c); read(d);
        int x = c ? c + h : a, y = d ? d : b + h;
        ++ deg[x]; -- deg[y]; E[x].PB(y); E[y].PB(x);
    }
    for(int i = 1;i <= h;++ i) if(deg[i] < 0 || deg[i+h] > 0){puts("NO"); return 0;}
    for(int i = 1;i <= (h<<1);++ i)
        if(!E[i].empty() && !vis[i]){flg = false; dfs(i); if(!flg){puts("NO"); return 0;}}
    puts("YES");
}

AGC018

C Coins

题目描述：给定 \(X+Y+Z\) 个三元组 \((a_i,b_i,c_i)\)，你要把它们分成三组，分别有 \(X,Y,Z\) 个，求第一组的 \(a\) 之和+第二组的 \(b\) 之和+第三组的 \(c\) 之和的最大值。

数据范围：\(X+Y+Z\le 10^5,a_i,b_i,c_i\le 10^9\)。

solution

对于只有两元的问题，直接按 \(a_i-b_i\) 排序，前面的选 \(a\)，后面的选 \(b\) 是最优的。

对于原问题，容易想到将所有的三元组按 \(a_i-b_i\) 排序，那么存在一个分界点 \(p\)，使得前面没有 \(b\)，后面没有 \(a\)。这就是一个二元子问题，使用堆优化插入即可。时间复杂度 \(O(n\log n)\)。

## AGC019

C Fountain Walk

题目描述：一个奇妙图上的最短路。

solution

首先可以通过对称性使 \(x_1\le x_2,y_1\le y_2\)。

分析一下性质，发现绕半圆对答案的增加<绕1/4圆对答案的减少，且不能为了 Fountain 绕路（必定按曼哈顿距离的路径走）。

问题就转化为了求最长上升子序列。

#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 200003;
const double pi = acos(-1);
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, k, xa, ya, xb, yb, q[N], dp[N], len; pii p[N];
int main(){
    read(xa); read(ya); read(xb); read(yb); read(n);
    for(int i = 1;i <= n;++ i){read(p[i].fi); read(p[i].se);}
    if(xa > xb){swap(xa, xb); swap(ya, yb);}
    if(ya > yb){
        for(int i = 1;i <= n;++ i) p[i].se = 1e8 + 1 - p[i].se;
        ya = 1e8 + 1 - ya; yb = 1e8 + 1 - yb;
    } sort(p + 1, p + n + 1);
    for(int i = 1;i <= n && p[i].fi <= xb;++ i)
        if(p[i].fi >= xa && p[i].se >= ya && p[i].se <= yb)
            q[++k] = p[i].se;
    dp[0] = -1;
    for(int i = 1;i <= k;++ i)
        if(dp[len] < q[i]) dp[++len] = q[i];
        else dp[lower_bound(dp + 1, dp + len + 1, q[i]) - dp] = q[i];
    printf("%.12lf\n", pi * 5 * (len == xb - xa + 1 || len == yb - ya + 1) + 100ll * (xb - xa + yb - ya) + (pi * 5 - 20) * len);
}

D Shift and Flip

题目描述：给定两个 \(01\) 字符串 \(A,B\)，可以做如下操作：

\(A\) 左移一位。
\(A\) 右移一位。
若 \(B_i=1\)，将 \(A_i\) 反转。

求把 \(A\) 变为 \(B\) 的最小操作次数。需判断无解。

数据范围：\(|A|=|B|\le 2000\)。

solution

容易知道有解当且仅当 \(A=B\) 或 \(B\) 中有 \(1\)。

为了实现方便，可以将 \(B\) 复制 3 份。

首先枚举一下最终的偏移量 \(mv\)，表示最后 \(A\) 总体往左/右移动了 \(mv\) 位。

若 \(A_i=B_{i+mv}\) 则不用反转，否则需要转到一个 \(B\) 为 \(1\) 的位置反转。

对于这些需要反转的位置，若中途经过过 \(B\) 为 \(1\) 的位置，则不用管，否则要多向左/右移动，计算出二元组 \((l,r)\) 表示到达 \(B\) 为 \(1\) 的位置要向左走 \(l\) 步或向右走 \(r\) 步。

要计算的即为哪些向左，哪些向右，操作次数为两者的最大值之和。排序+遍历即可，时间复杂度 \(O(n^2\log n)\)。

#include<bits/stdc++.h>
#define MP make_pair
#define PB push_back
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 6003, INF = 0x3f3f3f3f;
int n, cnt[N], L[N], R[N], ans = INF;
char a[N], b[N];
bool flg = true;
vector<pii> tmp;
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int main(){
    scanf("%s%s", a+1, b+1); n = strlen(a+1);
    for(int i = 1;i <= n;++ i){
        b[i+(n<<1)] = b[i+n] = b[i];
        flg &= a[i] == b[i];
    } if(flg){puts("0"); return 0;}
    for(int i = 1;i <= 3*n+1;++ i)
        cnt[i] = cnt[i-1] + (b[i] == '1');
    if(!cnt[n]){puts("-1"); return 0;} L[0] = -INF;
    for(int i = 1;i <= 3*n;++ i) L[i] = b[i] == '1' ? i : L[i-1];
    R[3*n+1] = INF;
    for(int i = 3*n;i;-- i) R[i] = b[i] == '1' ? i : R[i+1];
    for(int mv = -n;mv <= n;++ mv){
        tmp.clear(); tmp.PB(MP(0, 0));
        int tot = 0, mxr = 0, tans = INF;
        for(int i = 1;i <= n;++ i) if(a[i] != b[i+mv+n]){
            ++ tot; int l = i + mv + n, r = i + n;
            if(l > r) swap(l, r);
            if(cnt[r] == cnt[l-1])
                tmp.PB(MP(l - L[l], R[r] - r));
        } sort(tmp.begin(), tmp.end());
        for(int i = tmp.size()-1;i >= 0 && mxr < INF;-- i){
            if(tmp[i].fi != -INF)
                chmin(tans, tmp[i].fi + mxr);
            chmax(mxr, tmp[i].se);
        } chmin(ans, tot + abs(mv) + (tans<<1));
    } printf("%d\n", ans);
}

E Shuffle and Swap

题目描述：给定两个 \(01\) 字符串 \(A,B\)，设 \(\{a\}_{i=1}^k,\{b\}_{i=1}^k\) 分别是 \(A,B\) 中 \(1\) 的下标构成的序列。对 \(A\) 按顺序做如下操作：

将 \(a,b\) random_shuffle。
\(\text{for} \ i=1\rightarrow n,\text{swap}(A_{a_i},A_{b_i})\)。

求 \(P(A=B)\times (k!)^2\bmod 998244353\)。

数据范围：\(1\le |A|=|B|\le 10^4\)，\(A,B\) 中 \(1\) 的个数相同且至少有 \(1\) 个。

~~还是没掌握计数题的套路，我壬傻了。~~

Tips:这种交换操作序列的问题，考虑每个元素的移动，就可以变为有向链。

solution

\(A_i=B_i=0\) 的点与世隔绝，直接忽略。

考虑转化一下题面，设 \(A_i=B_i=1\) 的点为 P（公共点），设有 \(s\) 个。\(A_i=0,B_i=1\) 的点为 S（起点），\(A_i=1,B_i=0\) 的点为 E（终点）。容易知道 S 与 E 个数相等，设为 \(t\)。

若把 \(a_i\rightarrow b_i\) 连边（不考虑 \(1\) 与 \(1\) 交换），最终形成的是一堆链，从 S 到 E，中间经过一堆 P。

考虑 dp，每次插入一个点。\(f_{i,j}\) 表示用了 \(i\) 个 P，形成 \(j\) 条链的方案数。

插入一个 P 在链尾，方案数是 \(j\)，标号数是 \(i\)，即 \(f_{i,j}\leftarrow ijf_{i-1,j}\)。
新开一个链，S 与 E 的标号数是 \(j^2\)，即 \(f_{i,j}\leftrightarrow j^2f_{i,j-1}\)。

合在一起即为初值 \(f_{0,0}=1\)，转移方程

\[f_{i,j}=ijf_{i-1,j}+j^2f_{i,j-1} \]

最终答案是考虑多余交换的方案数，并合并成一个序列。

\[ans=\sum_{i=0}^s\binom si\times(i!)^2\times f_{s-i,t}\times \binom{s+t}i \]

时间复杂度 \(O(n^2)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10003, mod = 998244353;
int n, A, B, fac[N], inv[N], f[N][N], ans; char a[N], b[N];
int ksm(int a, int b){
    int res = 1;
    for(;b;b >>= 1, a = (LL) a * a % mod)
        if(b & 1) res = (LL) res * a % mod;
    return res;
}
int C(int n, int m){return (LL) fac[n] * inv[m] % mod * inv[n-m] % mod;}
int main(){
    scanf("%s%s", a+1, b+1); n = strlen(a+1); fac[0] = 1;
    for(int i = 1;i <= n;++ i) fac[i] = (LL) fac[i-1] * i % mod;
    inv[n] = ksm(fac[n], mod-2);
    for(int i = n;i;-- i) inv[i-1] = (LL) inv[i] * i % mod;
    for(int i = 1;i <= n;++ i) if(a[i] == '1')
        if(b[i] == '1') ++ A; else ++ B;
    f[0][0] = 1;
    for(int i = 0;i <= A;++ i)
        for(int j = 0;j <= B;++ j){
            if(i) f[i][j] = (LL) f[i-1][j] * i % mod * j % mod;
            if(j) f[i][j] = (f[i][j] + (LL) f[i][j-1] * j % mod * j) % mod;
        }
    for(int i = 0;i <= A;++ i)
        ans = (ans + (LL) inv[A-i] % mod * fac[i] % mod * f[A-i][B] % mod * C(A+B, i)) % mod;
    printf("%lld\n", (LL) ans * fac[A] % mod);
}

F Yes or No

题目描述：给定一场有 \(n+m\) 道判断题的考试，你已知有 \(n\) 个题选 ✔，\(m\) 个题选 ✘，按顺序回答每道题，回答完一题就能得到该题答案，求最优策略下期望答对题目数\(\bmod 998244353\)。

数据范围：\(n,m\le 5\cdot 10^5\)。

如果想直接暴推柿子就拿凉心出题人送的部分分吧（

solution

不妨设 \(n\ge m\)。容易发现最优解一定是回答剩下较多的答案。

将整个过程看作 \((n,m)\rightarrow (0,0)\) 的路径，向左走是 Yes，向下走是 No。如果你一直不经过 \(y=x\) 这条折线，那么就会一直回答 Yes，答案就是 \(n\)，否则经过之后，将剩下的路径做对称，除了 \(y=x\) 之外其他点的贡献总和就是 \(n\)，\(y=x\) 上的点的贡献即为

\[\frac{\sum_{k=1}^m\binom{n-k+m-k}{n-k}\binom{2k}k}{2\binom{n+m}{m}} \]

时间复杂度 \(O(n)\)。

Tips:不要只管推柿子而忘了组合意义...

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1000003, mod = 998244353;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int ksm(int a, int b){
    int res = 1;
    for(;b;b >>= 1, a = (LL) a * a % mod)
        if(b & 1) res = (LL) res * a % mod;
    return res;
}
int n, m, fac[N], inv[N], ans;
void init(int m){
    fac[0] = 1;
    for(int i = 1;i <= m;++ i) fac[i] = (LL) fac[i-1] * i % mod;
    inv[m] = ksm(fac[m], mod-2);
    for(int i = m;i;-- i) inv[i-1] = (LL) inv[i] * i % mod;
}
int C(int a, int b){return (LL) fac[a+b] * inv[a] % mod * inv[b] % mod;}
int main(){
    read(n); read(m); init(n+m);
    if(n < m) swap(n, m);
    for(int i = 1;i <= m;++ i)
        ans = (ans + (LL) C(n-i, m-i) * C(i, i)) % mod;
    if(ans & 1) ans += mod; ans >>= 1;
    printf("%lld\n", ((LL) ans * ksm(C(n, m), mod-2) + n) % mod);
}

AGC021

D Reversed LCS

lcs=longest common sequence, lps=longest palindrome sequence.

题目描述：给定字符串 \(S\) 和正整数 \(k\)，求更改至多 \(k\) 个字符的情况下，\(\text{lcs}(S,S^R)\) 的最大值。

数据范围：\(0\le k\le |S|\le 300\)。

solution

根据这篇题解，\(\text{lcs}(S,S^R)=\text{lps}(S)\)。于是直接区间 DP，设 \(f_{l,r,k}\) 表示区间 \([l,r]\) 内修改 \(k\) 个字符的 \(\text{lps}\) 长度。

时间复杂度 \(O(k|S|^2)\)。

## AGC022

D Shopping

题目描述：给定 \(n\) 个购物点 \(x_i\) 和对应的购物时间 \(t_i\)。一辆列车从 \(0\) 开始在 \([0,L]\) 往返跑，一开始在 \(0\)。求在购物不间断的情况下，乘坐列车完成购物并回到原点的最少时间。

数据范围：\(n\le 3\times 10^5,0<x_1<\dots<x_n<L\le 10^9,t_i\le 10^9\)。

solution

容易知道答案是 \(2L\) 乘上来回数。容易知道可以令 \(ans\leftarrow2L\lfloor\frac{t_i}{2L}\rfloor,t_i:=t_i\bmod 2L\)。然后把 \(t_i=0\) 的点去除。

此时 \(t_i<2L\)，来回数有一个上界 \(n+1-[t_n\le 2(L-x_n)]\)：从左至右依次直接下车购物，转一圈之后跑路。

然后就可以把前 \(n-1\) 个购物点分为 \(3\) 类：

\(t_i\le 2x_i\)，分为 A 类。
\(t_i\le 2(L-x_i)\)，分为 B 类。
同时属于 A,B，将其从 A,B 中去除，分为 C 类。

\(t_i>2\max(x_i,L-x_i)\) 的点对减少答案没有用处，忽略掉。

然后就能发现一个 \(A-C,C-B,C-C\) 的匹配能使来回数-1。

由于 A 类都 \(x_i>\frac L2\)，B 类都 \(x_i<\frac L2\)，所以可以将 A 类从大到小排序，B 类从小到大排序，然后贪心跟 C 匹配。

时间复杂度 \(O(n\log n)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 300003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, L, x[N], ans; set<int> B, C; set<int, greater<int> > A;
int main(){
    read(n); read(L); L <<= 1; ans = n+1;
    for(int i = 1;i <= n;++ i) read(x[i]);
    for(int i = 1, x, t;i <= n;++ i){
        read(t); x = ::x[i]; ans += t / L; t %= L;
        bool f1 = t <= (x<<1), f2 = t <= L - (x<<1);
        if(!t || i == n && f2){-- ans; continue;}
        if(f1 && f2) C.insert(x);
        else if(f1) A.insert(x);
        else if(f2) B.insert(x);
    }
    for(int t : B) if(!C.empty() && *C.begin() < t){C.erase(C.begin()); -- ans;}
    for(int t : A) if(!C.empty() && *C.rbegin() > t){C.erase(*C.rbegin()); -- ans;}
    ans -= C.size() >> 1;
    printf("%lld\n", (LL) ans * L);
}

F Checkers

题目描述：给定 \(n\) 个点，初始第 \(i\) 个点在 \(X^i\)（数轴上）。进行以下操作 \(n-1\) 次：选择两个点 \(a,b\)，将 \(a\) 移动到对 \(b\) 的对称点，删除 \(b\)。问最后剩下的点的可能位置数量\(\bmod(10^9+7)\)。

数据范围：\(X=10^{100},n\le 50\)。

solution

Tips:要多尝试一些转化方法，不然就暴毙了。

发现这个过程类似一个 Huffman 树~~然后就不会做了~~

显然只需考虑最后每个点的贡献系数。这些贡献系数形如 \(\pm 2^k\)。

考虑换一种转化方法，设上述操作 \(a,b\)，连边 \(a\rightarrow b\)，最后 \(2\) 的幂次就是深度，只需考虑每个深度的点的正负个数。

容易发现，\(-1\) 的幂次即为：儿子个数+所有祖先在操作了当前儿子之后的儿子个数。

向父亲差分后方案数不变，变为：儿子个数+父亲之前操作的儿子个数+1。

然后就可以按深度从小到大 dp，设 \(f_{i,j}\) 表示当前有 \(i\) 个点，最后一层有 \(j\) 个点钦定要有奇数个儿子。枚举当前这一层下要挂的点数 \(k\)，则 \(2|(k-j)\) 且 \(\frac{k-j}2\) 个点的差分（目前的）为 \(0\)。枚举这一层实际上有 \(t\) 个点差分值为 \(0\)，则当前至少有 \(|t-\frac{k-j}2|\) 个点有奇数个儿子。

据题解说，只需考虑恰好 \(|t-\frac{k-j}2|\) 个点的情况。因为其他情况都会算重。

在其它情况中，为了保持最后差分为1的点的数量不变，每次必然会钦定两个差分不同的儿子将会有奇数个儿子

此时我们直接交换这两个点的操作顺序，并将其中一个点的所有儿子合并到另一个点的儿子里面，可以保持所有点的符号不变，即答案不变。因此不能算这种情况，会导致重复计数。

也因此得到，转移系数直接用组合数搞，即

\[f_{i+j,|t-\frac{k-j}2|}\leftrightarrow\binom{n-i}j\binom jtf_{i,k} \]

（前一个系数是标号数，后一个系数是选择 \(t\) 个点改变差分）时间复杂度 \(O(n^4)\)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 53, mod = 1e9 + 7;
int n, fac[N], inv[N], f[N][N];
int ksm(int a, int b){int res = 1; for(;b;b >>= 1, a = (LL) a * a % mod) if(b & 1) res = (LL) res * a % mod; return res;}
int C(int a, int b){if(a < b || b < 0) return 0; return (LL) fac[a] * inv[b] % mod * inv[a-b] % mod;}
int main(){
    scanf("%d", &n); fac[0] = 1;
    for(int i = 1;i <= n;++ i) fac[i] = (LL) fac[i-1] * i % mod;
    inv[n] = ksm(fac[n], mod-2);
    for(int i = n;i;-- i) inv[i-1] = (LL) inv[i] * i % mod;
    f[1][0] = f[1][1] = n;
    for(int i = 1;i < n;++ i)
        for(int j = 1;j <= n-i;++ j)
            for(int k = j&1;k <= j;k += 2){
                int d = j - k >> 1;
                for(int t = 0;t <= j;++ t){
                    int u = abs(t - d);
                    f[i+j][u] = (f[i+j][u] + (LL) C(n-i, j) * C(j, t) % mod * f[i][k]) % mod;
                }
            }
    printf("%d\n", f[n][0]);
}

AGC023

E Inversions

题目描述：给定长为 \(n\) 的正整数序列 \(a\)，求所有满足 \(p_i\le a_i\) 的排列 \(p\) 的逆序对个数之和\(\bmod(10^9+7)\)。

数据范围：\(n\le 2\times 10^5\)。

solution

设 \(cnt_i=\sum_j[a_j\ge i]\)，则排列个数为 \(S=\prod_{i=1}^n(cnt_i-n+i)\)。

枚举逆序对 \((i,j)\)，设 \(i<j,p_i>p_j\)，计算有多少个排列满足此条件。

若 \(a_i\le a_j\)，则 \(p_j<a_i\)，将 \(a_j:=a_i\) 之后答案即为此时排列个数\(/2\)。

若 \(a_i>a_j\)，反面考虑之后同理。

设 \(D_i=\frac{cnt_j-n+j-1}{cnt_j-n+j}\)，则此时排列个数为 \(S\times \prod_{k=a_i+1}^{a_j}D_k\)。求前缀积后枚举较大的 \(a\)，用树状数组求和即可。

\(D_i=0\) 的位置要特殊处理。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200003, mod = 1e9 + 7;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
void qmo(int &x){x += x >> 31 & mod;}
int ksm(int a, int b){int res = 1; for(;b;b >>= 1, a = (LL) a * a % mod) if(b & 1) res = (LL) res * a % mod; return res;}
int n, a[N], cnt[N], d[N], id[N], all = 1, pre[N], pos[N], ans;
struct BIT {
    int tr[N];
    void clear(){memset(tr, 0, n+1<<2);} BIT(){clear();}
    void upd(int p, int v){v -= mod; for(;p <= n;p += p & -p) qmo(tr[p] += v);}
    int qry(int p){int r = 0; for(;p;p -= p & -p) qmo(r += tr[p] - mod); return r;}
} t1, t2;
int main(){
    read(n);
    for(int i = 1;i <= n;++ i){read(a[i]); ++ cnt[a[i]];}
    for(int i = n-1;i;-- i) cnt[i] += cnt[i+1];
    for(int i = 1;i <= n;++ i) all = (LL) all * (cnt[i] -= n-i) % mod;
    if(!all){puts("0"); return 0;} pos[0] = d[0] = 1;
    for(int i = 1;i <= n;++ i){
        int x = (cnt[i]-1ll) * ksm(cnt[i], mod-2) % mod;
        if(x){pre[i] = pre[i-1]; d[i] = (LL) d[i-1] * x % mod;}
        else {pos[pre[i] = pre[i-1] + 1] = i; d[i] = d[i-1];}
        id[i] = ksm(d[i], mod-2);
    }
    for(int i = 1;i <= n;++ i){
        int tmp = (LL)(t1.qry(a[i]) + mod - t1.qry(pos[pre[a[i]]]-1)) * d[a[i]] % mod;
        if(tmp & 1) tmp += mod; tmp >>= 1; qmo(ans += tmp - mod); t1.upd(a[i], id[a[i]]);
    } t1.clear();
    for(int i = n;i;-- i){
        int tmp = (LL)(t1.qry(a[i]-1) + mod - t1.qry(pos[pre[a[i]]]-1)) * d[a[i]] % mod;
        if(tmp & 1) tmp += mod; tmp >>= 1; qmo(ans -= tmp); qmo(ans += t2.qry(a[i]-1) - mod);
        t1.upd(a[i], id[a[i]]); t2.upd(a[i], 1); 
    } printf("%lld\n", (LL) ans * all % mod);
}

F 01 on Tree

题目描述：给定 \(n\) 个点的树，每个点有 \(01\) 权值，求以 \(1\) 为根的拓扑序的逆序对个数的最小值。

数据范围：\(n\le 2\times 10^5\)。

solution

考虑整体合并过程，\(A\) 放在 \(B\) 前面当且仅当 \(\frac{A_0}{A_1}>\frac{B_0}{B_1}\)。

每次找到 \(\frac{A_0}{A_1}\) 最小的点，和父亲合并。注意相同时要取最深的一个。用堆+并查集维护，时间复杂度 \(O(n\log n)\)。

注意 stl 的比较类调用非 const 会在 C++17/20 上报错...

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, fa[N], cnt[2][N], rt[N]; LL ans;
int get(int x){return x == rt[x] ? x : rt[x] = get(rt[x]);}
struct Ver {
    int u; Ver(int _u = 0): u(_u){}
    bool operator == (const Ver &b){return u == b.u;}
    bool operator < (const Ver &b) const {
        LL t1 = (LL) cnt[0][u] * cnt[1][b.u], t2 = (LL) cnt[1][u] * cnt[0][b.u];
        if(t1 != t2) return t1 > t2; return u > b.u;
    }
}; set<Ver> S;
int main(){
    read(n);
    for(int i = 2;i <= n;++ i) read(fa[i]);
    for(int i = 1, x;i <= n;++ i){read(x); rt[i] = i; cnt[x][i] = 1;}
    for(int i = 2;i <= n;++ i) S.insert(Ver(i));
    while(!S.empty()){
        int now = S.begin()->u; S.erase(S.begin());
        int fat = get(fa[now]); S.erase(Ver(fat));
        ans += (LL) cnt[1][fat] * cnt[0][now];
        cnt[0][fat] += cnt[0][now]; cnt[1][fat] += cnt[1][now];
        rt[now] = fat; if(fat > 1) S.insert(Ver(fat));
    } printf("%lld\n", ans);
}

AGC025

E Walking on a Tree

题目描述：给定 \(n\) 个点的树和 \(m\) 条链 \((u,v)\)，要求给这 \(m\) 条链定向，使得每条边的经过方向数(0/1/2)之和尽量大。

数据范围：\(n,m\le 2000\)。

solution

大概也是经典题了，之前好像听别人讲过？

答案必定是 \(\sum \min(2,c_e)\)，其中 \(c_e\) 表示边 \(e\) 的经过次数。考虑构造：对于叶子 \(u\) 和与其相连的唯一点 \(v\)，

若 \(c_{u,v}=0\)，则直接删掉 \(u\) 对答案无影响。
若 \(c_{u,v}=1\)，设唯一的一条链是 \([u,a]\)，改为 \([v,a]\) 再删掉 \(u\)，答案 +1。
若 \(c_{u,v}\ge 2\)，设其中两条链是 \([u,a]\) 和 \([b,u]\)，交点是 \(d\)，则 \([u,d]\) 上的所有边必定被经过两个方向，按 2. 中的方法依次处理，这两条链直接改为 \([a,b]\) 对答案无影响。

使用 set 维护每个点为端点的链，时间复杂度 \(O(n\log^2 n)\) （暴力启发式合并）或 \(O(n\log n)\)。

具体实现来说，可以对于每个端点维护方向，去除直上直下的链，限制即为 \([u,v]\) 要求 \(u,v\) 方向不同。

#include<bits/stdc++.h>
#define MP make_pair
#define PB emplace_back
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 2003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, cnt, head[N], to[N<<1], nxt[N<<1], res, col[N<<1], fa[11][N], dep[N], v[2][N], sum[N];
set<pii> S[N]; vector<pii> del[N]; vector<int> G[N<<1];
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
void dfs(int x){
    for(int i = 1;i < 11;++ i) fa[i][x] = fa[i-1][fa[i-1][x]];
    for(int i = head[x];i;i = nxt[i]) if(to[i] != fa[0][x]){
        dep[to[i]] = dep[x] + 1; fa[0][to[i]] = x; dfs(to[i]);
    }
}
int lca(int u, int v){
    if(dep[u] < dep[v]) swap(u, v);
    for(int i = 10;~i;-- i)
        if(dep[fa[i][u]] >= dep[v]) u = fa[i][u];
    for(int i = 10;~i;-- i)
        if(fa[i][u] != fa[i][v]){u = fa[i][u]; v = fa[i][v];}
    return u == v ? u : fa[0][u];
}
void work(int x){
    int tmp = 0;
    for(int i = head[x];i;i = nxt[i]) if(to[i] != fa[0][x]){
        work(to[i]); if(S[to[i]].size() == 1) ++ res;
        else if(S[to[i]].size() > 1){
            res += 2;
            if(!sum[to[i]]){
                auto t0 = S[to[i]].begin(), t1 = next(t0);
                G[t0->se].PB(t1->se); G[t1->se].PB(t0->se);
                int x = t0->fi, y = t1->fi;
                if(dep[x] > dep[y]) swap(x, y);
                ++ sum[to[i]]; -- sum[y];
            }
        } sum[x] += sum[to[i]];
        if(!tmp || S[tmp].size() < S[to[i]].size()) tmp = to[i];
    } if(tmp) swap(S[x], S[tmp]);
    for(int i = head[x];i;i = nxt[i]) if(to[i] != fa[0][x]){
        for(pii u : S[to[i]]) S[x].insert(u); S[to[i]].clear();
    } for(pii u : del[x]) S[x].erase(u);
}
void dfsc(int x){for(int v : G[x]) if(col[v] == -1){col[v] = !col[x]; dfsc(v);}}
int main(){
    read(n); read(m);
    for(int i = 1, u, v;i < n;++ i){
        read(u); read(v); add(u, v); add(v, u);
    } fa[0][1] = 1; dfs(1);
    for(int i = 0;i < m;++ i){
        read(v[0][i]); read(v[1][i]);
        if(dep[v[0][i]] > dep[v[1][i]]) swap(v[0][i], v[1][i]);
        int tmp = lca(v[0][i], v[1][i]);
        S[v[1][i]].insert(MP(tmp, i<<1)); del[tmp].PB(tmp, i<<1);
        if(tmp != v[0][i]){
            S[v[0][i]].insert(MP(tmp, i<<1|1));
            G[i<<1].PB(i<<1|1); G[i<<1|1].PB(i<<1);
            del[tmp].PB(tmp, i<<1|1);
        }
    } work(1); memset(col, -1, sizeof col);
    for(int i = 0;i < (m<<1);++ i)
        if(col[i] == -1){col[i] = 0; dfsc(i);}
    printf("%d\n", res);
    for(int i = 0;i < m;++ i){
        bool f = col[i<<1];
        printf("%d %d\n", v[f][i], v[!f][i]);
    }
}

-F Addition and Andition

题目描述：给定正整数 \(a,b,k\)，做 \(k\) 次操作：将 \(a,b\) 都加上 \(a\&b\)。求最后的 \(a,b\)。

数据范围：\(a,b\le 2^{10^6},k\le 10^6\)。\(a,b\) 以二进制形式给出。

AGC026

E Synchronized Subsequence

题目描述：给定长为 \(2n\) 的字符串 \(S\)，求满足以下条件的字典序最大的子串 \(T\)：第 \(i\) 个 a 和第 \(i\) 个 b 都选或都不选。

数据范围：\(n\le 3000,S\) 中 ab 各有 \(n\) 个。

solution

设 \(f_i\) 表示只考虑第 \([i,n]\) 对 ab 时的答案。\(a_i,b_i\) 表示第 \(i\) 个 ab 的位置，则

第 \(i\) 对 ab 都不选，\(f_i=f_{i+1}\)。
第 \(i\) 对 ab 都选，且 \(a_i<b_i\)，则 \([a_i,b_i)\) 中的字符都是 a，应当尽量不选，于是 \(f_i=\texttt{ab}+f_{pos}\)，其中 \(pos\) 是第一个 \(\min(a_{pos},b_{pos})>b_i\) 的位置。
第 \(i\) 对 ab 都选，且 \(a_i>b_i\)，则 \([b_i,a_i)\) 中的字符都是 b，应当尽量选，然而选了更多对之后可能出现连锁反应，遍历一下算出取到哪里即可。

时空复杂度 \(O(n^2)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 6003;
int n, t1, t2, a[N], b[N], c[N]; char s[N]; string f[N]; bool vis[N];
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int main(){
    scanf("%d%s", &n, s+1);
    for(int i = 1;i <= (n<<1);++ i)
        if(s[i] == 'a') a[c[i] = ++t1] = i;
        else b[c[i] = ++t2] = i;
    for(int i = n;i;-- i){
        f[i] = f[i+1];
        if(a[i] < b[i]){
            int pos = i+1;
            while(pos <= n && min(a[pos], b[pos]) <= b[i]) ++ pos;
            chmax(f[i], "ab" + f[pos]);
        } else {
            int r = a[i]; string tmp;
            memset(vis, 0, sizeof vis);
            vis[a[i]] = vis[b[i]] = true;
            for(int j = b[i]+1;j < r;++ j)
                if(s[j] == 'b'){
                    chmax(r, a[c[j]]);
                    vis[j] = vis[a[c[j]]] = true;
                }
            for(int j = b[i];j <= (n<<1);++ j) if(vis[j]) tmp += s[j];
            int pos = c[r] + 1;
            while(pos <= n && min(a[pos], b[pos]) <= b[i]) ++ pos;
            chmax(f[i], tmp + f[pos]);
        }
    } cout << f[1] << endl;
}

F Manju Game

题目描述：给定一个长为 \(n\) 的正整数序列，Alice 与 Bob 轮流操作，Alice 先手，轮流进行 \(n\) 次操作：选择一个之前未选中的数，且与上一个玩家选择的数相邻（如果是第一次或者上一次选择的数周围没有未被选中的数，则可以任意选择一个数）

两个人都想要最大化自己所选择的数之和，且都采取最优策略，求最后 Alice 选择的数之和与 Bob 选择的数之和。

数据范围：\(n\le 3\times 10^5,a_i\le 10^3\)。

solution

题目即为做以下两种操作的博弈：

先手选择开头或结尾，先手取奇数位，后手取偶数位，结束。
先手选择中间的起始位置，后手选择方向，一直取过去。

由于 \(n\) 为偶数时做操作 2 会让后手占据先手地位，显然没有操作 1 优，所以直接做操作 1 即可。

然后考虑 \(n\) 为奇数的情况。这个游戏就变为以下操作：

先手选择奇数位，后手拿偶数位，游戏结束。
先手选择偶数位的分界点，后手选择方向，递归到区间的子问题。

于是就能得到先手取的数一定形如 \([1,l)\) 和 \((r,n]\) 上的偶数位和 \([l,r]\) 上的奇数位。先手希望最大化 \([l,r]\) 上的奇数位-偶数位之和。

由于每次是由后手选择方向，问题转化为先手选择一堆偶数位的分界点，取其中奇数位-偶数位之和的最小值。

先手想让最小值最大，考虑二分答案 \(mid\)，从左往右做，维护当前分界点的前缀和的最小值 \(mn\)，若 \(s_i-mn\ge mid\) 则 \(i+1\) 可以作为分界点。可行即为 \(n+1\) 可以作为分界点。时间复杂度 \(O(n\log V)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 300003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, a[N], sum[N], A, B;
bool check(int val){
    int mn = 0;
    for(int i = 1;i < n;i += 2)
        if(sum[i] - mn >= val)
            chmin(mn, sum[i+1]);
    return sum[n] - mn >= val;
}
int main(){
    read(n);
    for(int i = 1;i <= n;++ i){
        read(a[i]); sum[i] = sum[i-1];
        if(i & 1){sum[i] += a[i]; A += a[i];}
        else {sum[i] -= a[i]; B += a[i];}
    }
    if(!(n & 1)){printf("%d %d\n", max(A, B), min(A, B)); return 0;}
    int l = 1, r = A, mid, ans = 0;
    while(l <= r){
        mid = l + r >> 1;
        if(check(mid)){ans = mid; l = mid+1;}
        else r = mid-1;
    } printf("%d %d\n", B + ans, A - ans);
}

AGC027

E ABBreviate

题目描述：给定字符串 \(S\)，可以做任意次操作：\(aa\rightarrow b\) 或 \(bb\rightarrow a\)。求能得到的字符串数量\(\bmod(10^9+7)\)。

数据范围：\(|S|\le 10^5,\Sigma=\{a,b\}\)。

solution

首先特判掉 \(S\) 是 ab 交替，答案是 \(1\)。

容易发现，若分别将 \(a,b\) 看作 \(\pm 1\)，操作维持和\(\bmod 3\) 的余数不变，我们记这个数为 \(p(S)\)。

不容易发现，\(S\) 能变为字符 \(c\) 当且仅当 \(S=c\or p(S)=p(c)\and S\) 不是 ab 交替。

然后如何判断字符串 \(T\) 是否合法呢？将 \(S\) 划分成 \(|T|\) 段，每段的和\(\bmod 3\) 与字符串 \(T\) 对应。

如何保证计数不算重？从左往右贪心匹配最短的段，最右边剩下一个和为 \(0\) 的段。

简单 dp 即可解决，时间复杂度 \(O(|S|)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 100003, mod = 1e9 + 7;
int n, a[N], nxt[3][N], f[N], ans; char s[N]; bool flg = true;
void qmo(int &x){x += x >> 31 & mod;}
int main(){
    scanf("%s", s+1); n = strlen(s+1);
    for(int i = 1;i < n;++ i) flg &= s[i] != s[i+1];
    if(flg){puts("1"); return 0;}
    for(int i = 1;i <= n;++ i) a[i] = (a[i-1] + s[i] - 'a' + 1) % 3;
    for(int i = 0;i < 3;++ i) nxt[i][n] = n+1;
    for(int i = n-1;~i;-- i){
        for(int j = 0;j < 3;++ j) nxt[j][i] = nxt[j][i+1];
        nxt[a[i+1]][i] = i+1;
    } f[0] = 1;
    for(int i = 0;i < n;++ i){
        for(int j = 1;j <= 2;++ j)
            qmo(f[nxt[(a[i]+j)%3][i]] += f[i] - mod);
        if(i && a[i] == a[n]) qmo(ans += f[i] - mod);
    } qmo(ans += f[n] - mod); printf("%d\n", ans);
}

-F Grafting

题目描述：给定两棵 \(n\) 个点的有标号无根树 \(T_1,T_2\)，\(T_1\) 的每个节点初始都是白的。你可以对 \(T_1\) 做任意次操作，求将其形态变成 \(T_2\) 的最小操作次数（需判无解）\(T\) 组数据。

选择一个白色叶子 \(v\)；
删掉 \(v\) 连出的边，连向另一个点；
将 \(v\) 染成黑色。

数据范围：\(T\le 20,n\le 50\)。

AGC028

-F2 Reachable Cells

题目描述：给定 \(n\times n\) 的矩阵，每个元素是 \([1,9]\) 或 #（障碍），问所有满足 \(X\) 能向下或向右，不经过障碍，到达 \(Y\) 的网格对 \((X,Y)\) 的元素乘积之和。

数据范围：\(40\%:n\le 500,\text{TL}=4\text s;60\%:n\le 1500,\text{TL}=9\text s\)。

ARC104

-F Visibility Sequence

题目描述：给定长为 \(n\) 的正整数序列 \(X_i\)，对于所有满足 \(H_i\le X_i\) 的长度为 \(n\) 的正整数序列 \(H_i\)，求序列 \(P\) 的个数\(\bmod(10^9+7)\)，

\[P_i=\max\{j|j<i\and H_j>H_i\} \]

数据范围：\(n\le 100,X_i\le 10^5\)。

ARC105

E Keep Graph Disconnected

题目描述：给定 \(n\) 个点 \(m\) 条边的无向简单图，两人轮流操作，加一条边，不能使得图中有重边、自环或 \(1\) 与 \(n\) 连通，不能操作的人输，求谁必胜。\(T\) 组数据。

数据范围：\(2\le n\le 10^5,0\le m\le\min(\binom n2,10^5),\sum n,\sum m\le 2\times 10^5\)。

solution

最后的状态一定是两个完全图，所以 \(n\) 是奇数的时候无论怎样胜负已定。

此时考虑 \(\sum\binom{c_i}2-m\) 的奇偶性，其中 \(c_i\) 是每个连通块的大小。

若选择两个奇连通块相连，这个数的奇偶性不会变，胜负反转，否则一定会变。

设初始时奇连通块有 \(k\) 个，则 \(k\) 一定是偶数，则胜负会反转 \(\frac{k-1}2\) 或 \(\frac{k+1}2\) 次，前者表示最后 \(1\) 和 \(n\) 都处于奇连通块。

问题就转化为先/后手是否能让最后 \(1\) 和 \(n\) 都处于奇连通块，手玩一下就可以发现：

初始时 \(1,n\) 所在连通块奇偶性不同，则先手可以，后手不行。
初始时 \(1,n\) 所在连通块都是奇数，则都可以。
初始时 \(1,n\) 所在连通块都是偶数，则都不可以。

直接模拟这个过程即可，时间复杂度 \(O(n+m)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int t, n, m, cnt, cnt1, cnt2, head[N], to[N<<1], nxt[N<<1]; bool vis[N];
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
void dfs(int x){
    vis[x] = true; ++ cnt1;
    for(int i = head[x];i;i = nxt[i])
        if(!vis[to[i]]) dfs(to[i]);
}
void solve(){
    read(n); read(m); cnt = cnt1 = cnt2 = 0;
    memset(head, 0, n+1<<2); memset(vis, 0, n+1);
    for(int i = 1, u, v;i <= m;++ i){
        read(u); read(v); add(u, v); add(v, u);
    }
    if(n & 1){puts(((n-1>>1)^m)&1 ? "First" : "Second"); return;}
    dfs(n); swap(cnt1, cnt2); dfs(1);
    if((cnt1^cnt2)&1) puts("First");
    else puts(((n>>1)^m^cnt1)&1 ? "First" : "Second");
}
int main(){read(t); while(t --) solve();}

CF700E Cool Slogan

题目描述：给定字符串 \(S\)，求最大的正整数 \(k\)，使得存在长为 \(k\) 的非空字符串序列 \(s\)，使得 \(s_i\) 都是 \(S\) 的子串，且 \(s_{i-1}\) 在 \(s_i\) 中出现至少两次。

数据范围：\(|S|\le 2\times 10^5\)。

solution

建出 SAM 的 Parent 树，用主席树维护 endpos 集合。

从上至下 dp，设 \(f_i\) 表示到节点 \(i\) 时序列的长度，\(g_i\) 表示此时序列的末尾节点最浅的是哪个，转移状态直接贪心判断 \(g_{fa_i}\) 的字符串是否在 \(i\) 表示的字符串中出现至少 \(2\) 次。

时间复杂度 \(O(n\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 400003, M = N<<5;
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int n, rt[N], ls[M], rs[M], tot, ans;
char str[N];
void inse(int &x, int p, int L = 1, int R = n){
    if(!x) x = ++tot;
    if(L == R) return;
    int mid = L + R >> 1;
    if(p <= mid) inse(ls[x], p, L, mid);
    else inse(rs[x], p, mid+1, R);
}
void merge(int &x, int y){
    if(!x || !y){x ^= y; return;}
    int o = ++tot; ls[o] = ls[x]; rs[o] = rs[x]; x = o;
    merge(ls[x], ls[y]); merge(rs[x], rs[y]);
}
bool qry(int x, int l, int r, int L = 1, int R = n){
    if(!x) return false;
    if(l <= L && R <= r) return true;
    int mid = L + R >> 1;
    return l <= mid && qry(ls[x], l, r, L, mid) || mid < r && qry(rs[x], l, r, mid+1, R);
}
int ch[N][26], fa[N], len[N], pos[N], a[N], c[N], f[N], g[N], last = 1, cnt = 1;
void ins(int c, int id){
    int p = last, np = ++cnt; last = np; len[np] = len[p] + 1;
    pos[np] = id; inse(rt[np], id);
    for(;p && !ch[p][c];p = fa[p]) ch[p][c] = np;
    if(!p){fa[np] = 1; return;}
    int q = ch[p][c];
    if(len[q] == len[p] + 1){fa[np] = q; return;}
    int nq = ++cnt; len[nq] = len[p] + 1;
    memcpy(ch[nq], ch[q], sizeof ch[q]);
    fa[nq] = fa[q]; fa[q] = fa[np] = nq; pos[nq] = pos[q];
    for(;ch[p][c] == q;p = fa[p]) ch[p][c] = nq;
}
int main(){
    scanf("%d%s", &n, str+1);
    for(int i = 1;i <= n;++ i) ins(str[i] - 'a', i);
    for(int i = 1;i <= cnt;++ i) ++c[len[i]];
    for(int i = 1;i <= n;++ i) c[i] += c[i-1];
    for(int i = 1;i <= cnt;++ i) a[c[len[i]]--] = i;
    for(int i = cnt;i > 1;-- i) merge(rt[fa[a[i]]], rt[a[i]]);
    for(int i = 2;i <= cnt;++ i){
        int x = a[i];
        if(fa[x] == 1){f[x] = 1; g[x] = x;}
        else if(qry(rt[g[fa[x]]], pos[x] - len[x] + len[g[fa[x]]], pos[x] - 1)){
            f[x] = f[fa[x]] + 1; g[x] = x;
        } else {f[x] = f[fa[x]]; g[x] = g[fa[x]];}
        chmax(ans, f[x]);
    } printf("%d\n", ans);
}

-CF468E Permanent

题目描述：积和式 \(\bmod(10^9+7)\)。

数据范围：\(n\le 10^5\)，仅有至多 \(50\) 项非 \(1\)。

posted @ 2020-11-18 22:34 mizu164 阅读(251) 评论(0) 编辑收藏举报

刷新页面返回顶部

2020.11刷题记录

朱刘算法

CF671D Roads in Yusland

LOJ2842「JOISC 2018 Day 4」野猪

LOJ2836「JOISC 2018 Day 2」最差记者 3

CF1163F Indecisive Taxi Fee

LOJ2835「JOISC 2018 Day 2」路网服务

CODE FESTIVAL 2017 qual C

F Three Gluttons

AGC010

D Decrementing

E Rearranging

F Tree Game

AGC011

C Squared Graph

D Half Reflector

E Increasing Numbers

AGC012

C Tautonym Puzzle

D Colorful Balls

E Camel and Oases

AGC013

D Pilling Up

E Placing Squares

AGC015

D A or...or B Problem

AGC016

E Poor Turkeys

F Games on DAG

AGC017

C Snuke and Spells

D Game on Tree

E Jigsaw

AGC018

C Coins

C Fountain Walk

D Shift and Flip

E Shuffle and Swap

F Yes or No

AGC021

D Reversed LCS

D Shopping

F Checkers

AGC023

E Inversions

F 01 on Tree

AGC025

E Walking on a Tree

-F Addition and Andition

AGC026

E Synchronized Subsequence

F Manju Game

AGC027

E ABBreviate

-F Grafting

AGC028

-F2 Reachable Cells

ARC104

-F Visibility Sequence

ARC105

E Keep Graph Disconnected

CF700E Cool Slogan

-CF468E Permanent

公告