IOI2021 集训队作业

LOJ6405「ICPC World Finals 2018」征服世界

题目描述：给定 \(n\) 个点的树，边带权，初始第 \(i\) 个点有 \(x_i\) 个军队，最终要使第 \(i\) 个点至少有 \(y_i\) 个军队，求移动路程之和的最小值。

数据范围：\(n\le 2.5\times 10^5,\sum y_i\le\sum x_i\le 10^6,0\le c\le 10^6\)。

肝败吓疯...

这实际上是一个二分图匹配，考虑 dfs 枚举匹配的 lca，匹配的代价就是 \(dis(u,v)=dep_u+dep_v-2dep_{lca}\)，因为匹配的初始位置和目标位置在同一个子树时不优，所以不用考虑这种情况。

将每一个初始位置的权值 \(-\infty\)，这样每个初始位置就会被强制匹配。

一对已经在 \(z\) 处匹配的初始位置和目标位置不会同时反悔，所以元素入堆的总次数为 \(O(\sum x_i)\) 级别。

合并相同元素，使用可并堆维护，时间复杂度 \(O(n\log n)\)。

#include<bits/stdc++.h>
#include<ext/pb_ds/priority_queue.hpp>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 250003;
const LL inf = 1e12;
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, head[N], to[N<<1], nxt[N<<1], w[N<<1], a[N], b[N], s; LL ans;
void add(int a, int b, int c){
    static int cnt = 0;
    to[++ cnt] = b; nxt[cnt] = head[a]; head[a] = cnt; w[cnt] = c;
}
struct Node {
    LL val; mutable int cnt;
    Node(LL v = 0, int c = 0): val(v), cnt(c){}
    inline bool operator < (const Node &o) const {return val > o.val;}
}; __gnu_pbds::priority_queue<Node> p[N], q[N];
void dfs(int x, int f = 0, LL d = 0){
    p[x].push(Node(d, a[x])); q[x].push(Node(d - inf, b[x]));
    for(Rint i = head[x];i;i = nxt[i]) if(to[i] != f){
        dfs(to[i], x, d + w[i]); p[x].join(p[to[i]]); q[x].join(q[to[i]]);
    }
    while(!p[x].empty() && !q[x].empty()){
        Node t1 = p[x].top(), t2 = q[x].top();
        int cc = min(t1.cnt, t2.cnt); LL tmp = t1.val + t2.val - (d<<1);
        if(tmp >= 0) break; ans += cc * tmp;
        p[x].push(Node(t1.val - tmp, cc));
        q[x].push(Node(t2.val - tmp, cc));
        p[x].top().cnt -= cc; if(!p[x].top().cnt) p[x].pop();
        q[x].top().cnt -= cc; if(!q[x].top().cnt) q[x].pop();
    }
}
int main(){
    read(n);
    for(Rint i = 1, u, v, c;i < n;++ i){
        read(u); read(v); read(c); add(u, v, c); add(v, u, c);
    }
    for(Rint i = 1;i <= n;++ i){read(a[i]); read(b[i]); s += b[i];}
    dfs(1); printf("%lld\n", ans + s * inf);
}

LOJ6406「ICPC World Finals 2018」绿宝石之岛

题目描述：给定正整数 \(n,d,r\)，长为 \(n\) 的正整数序列 \(a\) 初始为 \(0\)，每次操作以 \(a_i+1\) 的权重随机一个整数 \(i\in[1,n]\)，然后将 \(a_i\) 加 \(1\)，求 \(d\) 次操作之后 \(a\) 中前 \(r\) 大的值的期望。

数据范围：\(n,d\le 500,r\le n\)。

对于一种局面 \(\sum a_i=d\)，出现这种局面的情况数是 \(\frac{d!}{\prod a_i!}\times\prod a_i!=d!\)，所以出现每种局面的概率相同！

然后就可以直接 dp，设 \(f_{i,j}\) 表示方案数，\(g_{i,j}\) 表示答案，其中 \(i,j\) 分别表示元素个数和 \(\sum a_i\)。枚举当前有 \(k\) 个最大值，然后减去 \(1\) 变为子问题。

\[\begin{aligned} f_{i,j}&=\sum_{k=0}^{\min(i,j)}\binom ikf_{k,j-k} \\ g_{i,j}&=\sum_{k=0}^{\min(i,j)}\binom ik(g_{k,j-k}+\min(k,r)f_{k,j-k}) \end{aligned} \]

时间复杂度 \(O(n^2d)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 503;
double c[N][N], f[N][N], g[N][N];
int n, d, r;
int main(){
    scanf("%d%d%d", &n, &d, &r); c[0][0] = f[0][0] = 1;
    for(Rint i = 1;i <= n;++ i){
        c[i][0] = 1;
        for(Rint j = 1;j <= i;++ j) c[i][j] = c[i-1][j-1] + c[i-1][j];
    }
    for(Rint i = 1;i <= n;++ i)
        for(Rint j = 0;j <= d;++ j)
            for(Rint k = 0;k <= i && k <= j;++ k){
                f[i][j] += c[i][k] * f[k][j-k];
                g[i][j] += c[i][k] * (g[k][j-k] + min(k,r) * f[k][j-k]);
            }
    printf("%.6lf\n", g[n][d] / f[n][d] + r);
}

LOJ6407「ICPC World Finals 2018」跳过罪恶

模拟题，代码咕了。

LOJ6410「ICPC World Finals 2018」单割故障

易(nan)得，答案 \(\le 2\)。

将矩形边界看作一个环，答案 \(=1\) 当且仅当存在一个区间满足其包含所有区间的恰好一个端点。直接枚举即可。

时间复杂度 \(O(n\log n)\)。你学废了么?

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 1000003;
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, w, h, cnt[N], now; pii a[N<<1];
int get(int x, int y){
    if(!y) return x;
    if(x == w) return w + y;
    if(y == h) return (w<<1) + h - x;
    return (w<<1) + (h<<1) - y;
}
void print(double p){
    if(p <= w) printf("%.1lf 0 ", p);
    else if(p <= w + h) printf("%d %.1lf ", w, p - w);
    else if(p <= (w<<1) + h) printf("%.1lf %d ", (w<<1) + h - p, h);
    else printf("0 %.1lf ", (w<<1) + (h<<1) - p)
}
int main(){
    read(n); read(w); read(h);
    for(Rint i = 0, x, y;i < (n<<1);++ i){
        read(x); read(y); a[i] = MP(get(x, y), i>>1);
    }
    sort(a, a + (n<<1));
    for(Rint i = 0;i < n;++ i) now += !cnt[a[i].se]++;
    for(Rint i = 0;i < n;++ i){
        if(now == n){puts("1"); print(a[i].fi - 0.5); print(a[i+n].fi - 0.5); return 0;}
        now -= !--cnt[a[i].se]; now += !cnt[a[i+n].se]++;
    }
    puts("2"); print(0.5); print(w + h + 0.5); putchar('\n'); print(w + 0.5); print((w<<1) + h + 0.5);
}

LOJ6470「ICPC World Finals 2017」机场构建

答案线段必定经过至少两个顶点（

直接暴力，时间复杂度 \(O(n^3)\)。

LOJ6473「ICPC World Finals 2017」不劳而获的钱财

题目描述：给定 \(m+n\) 个整点 \((x_i,y_i)\)，求

\[\max\{(x_j-x_i)(y_j-y_i)|1\le i\le m,m+1\le j\le m+n,x_i<x_j,y_i<y_j\} \]

数据范围：\(m,n\le 5\times 10^5,1\le x_i,y_i\le 10^9\)。

发现若 \(1\le i,j\le m\) 且 \(x_i\le x_j,y_i\le y_j\)，则 \(i\) 无用。 \(m+1\le i,j\le m+n\) 同理。

两部分都变为了 \(x\) 递增时 \(y\) 递减的，此时这个东西就是决策单调的。但此时条件要改为 \(x_i<x_j\or y_i<y_j\)，显然对答案没有影响但对计算决策点是有影响的。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 500003;
int m, n, tp; pii a[N], b[N], st[N]; LL ans;
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
void solve(int l, int r, int L, int R){
    if(l > r || L > R) return;
    int mid = l + r >> 1, nx = a[mid].fi, ny = a[mid].se, pos = L; LL res = -5e18;
    for(Rint i = L;i <= R;++ i)
        if((nx < b[i].fi || ny < b[i].se) && chmax(res, (LL) (b[i].fi - nx) * (b[i].se - ny))) pos = i;
    chmax(ans, res); solve(l, mid-1, L, pos); solve(mid+1, r, pos, R);
}
int main(){
    read(m); read(n);
    for(Rint i = 1;i <= m;++ i){read(a[i].fi); read(a[i].se);}
    for(Rint i = 1;i <= n;++ i){read(b[i].fi); read(b[i].se);}
    sort(a + 1, a + m + 1); tp = 1; st[1] = a[1]; sort(b + 1, b + n + 1);
    for(Rint i = 2;i <= m;++ i) if(a[i].se < st[tp].se) st[++tp] = a[i];
    for(Rint i = 2;i <= tp;++ i) a[i] = st[i]; m = tp; tp = 1; st[1] = b[1];
    for(Rint i = 2;i <= n;++ i){while(tp && b[i].se >= st[tp].se) -- tp; st[++tp] = b[i];}
    for(Rint i = 1;i <= tp;++ i) b[i] = st[i];
    solve(1, m, 1, tp); printf("%lld\n", ans);
}

LOJ6476「ICPC World Finals 2017」复制，复制，复制并变异

每次尝试缩起来，缩不起来就直接输出。

按照行列的两种顺序遍历能分别找到 bug 的所在行、列。

时间复杂度 \(O(wh\min(w,h))\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 303;
int m, n, o, xl = 1, xr, yl = 1, yr, tx, ty;
bool a[2][N][N];
char str[N];
bool CheckX(int x){for(Rint i = yl;i <= yr;++ i) if(a[o][x][i]) return false; return true;}
bool CheckY(int y){for(Rint i = xl;i <= xr;++ i) if(a[o][i][y]) return false; return true;}
bool get(int x, int y){bool r = a[o][x][y]; for(Rint i = -1;i <= 1;++ i) for(Rint j = -1;j <= 1;++ j) r ^= a[!o][x+i][y+j]; return r;}
int FindX(){
    memset(a[!o], 0, sizeof a[!o]);
    for(Rint i = xl;i <= xr;++ i)
        for(Rint j = yl;j <= yr;++ j)
            if((a[!o][i+1][j+1] = get(i, j)) && (i+1 >= xr || j+1 >= yr)) return i;
    return 0;
}
int FindY(){
    memset(a[!o], 0, sizeof a[!o]);
    for(Rint j = yl;j <= yr;++ j)
        for(Rint i = xl;i <= xr;++ i)
            if((a[!o][i+1][j+1] = get(i, j)) && (i+1 >= xr || j+1 >= yr)) return j;
    return 0;
}
int main(){
    scanf("%d%d", &m, &n);
    for(Rint i = 1;i <= n;++ i){
        scanf("%s", str + 1);
        for(Rint j = 1;j <= m;++ j) a[0][i][j] = str[j] == '#';
    } xr = n; yr = m;
    while(xl < xr - 1 && yl < yr - 1){
        if((tx = FindX()) && (a[o][tx][ty = FindY()] ^= 1, FindX())){a[o][tx][ty] ^= 1; break;}
        o ^= 1; while(CheckX(xl)) ++ xl; while(CheckX(xr)) -- xr; while(CheckY(yl)) ++ yl; while(CheckY(yr)) -- yr;
    }
    for(Rint i = xl;i <= xr;++ i){
        for(Rint j = yl;j <= yr;++ j) putchar(a[o][i][j] ? '#' : '.');
        putchar('\n');
    }
}

LOJ6480「ICPC World Finals 2017」弄虚作假的塔罗占卜

题目描述：给定 \(s\) 个长为 \(l\) 的字符串和正整数 \(n\)，将这 \(s\) 个字符串按在长为 \(n\) 的随机字符串中的出现概率排序。

数据范围：\(n\le 10^6,s\le 10,l\le 10^5,|\Sigma|=3\)。

直接上结论：按将 Border 长度从大到小排列得到的数列的字典序排序，注意要去掉不可能贡献答案的 border。

设无限随机字符串是 \(X\)，当前考虑的模式串是 \(P\)，\(M_P(i)\) 表示事件 \(X[i:i+l-1]=P\)。\(S\) 是 \(P\) 的 border 集合。\(f_S(n)\) 表示 \(\Pr[\bigcup\limits_{i=1}^nM_P(i)]\)，\(g_S(n)\) 表示 \(P\) 在位置 \(1\) 出现，但不在位置 \(2,\dots,n\) 出现的概率。

易得 \(f_S(n)=\sum_{i=1}^ng_S(i)\)。计算 \(g_S(n)\) 可以用容斥，对于 \(j\in[n-1]\)，\(P\) 在位置 \(1,j+1\) 出现，但不在 \(j+2,\dots,n\) 出现的概率为

\[\begin{cases} g_S(n-j)3^{-j} & \text{if }j<l,j\in S \\ g_S(n-j)3^{-l} & \text{if }j\ge l \\ 0 & \text{otherwise} \end{cases} \]

所以 \(g_S(n)=3^{-l}(1-\sum_{i=1}^{n-l}g_S(i))-\sum_{i\in S}3^{-i}g_S(n-i)\)。

所以 \(f_S(n)=3^{-l}(n-\sum_{i=1}^{n-l}f_S(i))-\sum_{i\in S}3^{-i}f_S(n-i)\)。

易得 \(g_S(n)\ge\frac23g_S(n-1)\)。

现在就来考虑那个结论了，设 \(S,T\) 是两个 Border 集合，设 \(\min(S\text{\\}T)>\min(T\text{\\}S)=r\)，则当 \(n\le r\) 时 \(f_S(n)=f_T(n)\)，\(n>r\) 时 \(f_S(n)>f_T(n)\)。

证明：设 \(D(n)=f_S(n)-f_T(n)\)。则

\[\begin{aligned} D(n)&=\sum_{i\in T}3^{-i}f_T(n-i)-\sum_{i\in S}3^{-i}f_S(n-i)-3^{-l}\sum_{i=1}^{n-l}D(i)\\ &=\sum_{i\in T\text{\\}S}3^{-i}f_T(n-i)-\sum_{i\in S\text{\\}T}3^{-i}f_S(n-i)-3^{-l}\sum_{i=1}^{n-l}D(i)-\sum_{i\in S\cap T}3^{-i}D(n-i) \\ &=\sum_{i\in T\text{\\}S}3^{-i}f_T(n-i)-\sum_{i\in S\text{\\}T}3^{-i}f_T(n-i)-3^{-l}\sum_{i=1}^{n-l}D(i)-\sum_{i\in S}3^{-i}D(n-i) \\ \Delta D(n)&=\sum_{i\in T\text{\\}S}3^{-i}g_T(n-i)-\sum_{i\in S\text{\\}T}3^{-i}g_T(n-i)-3^{-l}D(n-l)-\sum_{i\in S}3^{-i}\Delta D(n-i) \\ \end{aligned} \]

通过一些操作可以得出 \(D(n)\ge \frac 23D(n-1)\)，因为 \(n\le r\) 时 \(D(n)=0\)，\(D(r+1)=3^{-l-r}\)，得证。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 100003;
int n, m, l, id[N], nxt[N];
char s[10][N]; vector<int> v[10];
int main(){
    scanf("%d%d", &n, &m);
    for(Rint _ = 0;_ < m;++ _){
        scanf("%s", s[_] + 1); l = strlen(s[_] + 1); id[_] = _; nxt[0] = -1;
        for(Rint i = 1, j = -1;i <= l;++ i){while(~j && s[_][j+1] != s[_][i]) j = nxt[j]; nxt[i] = ++j;}
        for(Rint i = nxt[l];i && i >= 2 * l - n;i = nxt[i]) v[_].push_back(i);
    }
    stable_sort(id, id+m, [&](int x, int y){return v[x] < v[y];});
    for(Rint _ = 0;_ < m;++ _) printf("%s\n", s[id[_]] + 1);
}

LOJ6481「ICPC World Finals 2017」Visual Python++

题目描述：二维括号匹配。构造任意一种方案或判断无解。

数据范围：\(n\le 10^5\)。

不难发现匹配是唯一的，因为若构造出了一种方案，无论怎么交换匹配都会破坏原本的结构？

按照水平序排序，贪心选最近的点匹配，再用扫描线判断相交。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 200003;
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
void EE(){puts("syntax error"); exit(0);}
int n, m, t, id[N], mat[N]; pii a[N], add[N], del[N]; pair<int, pii> q[N]; set<pii> S; set<int> SS;
int main(){
    read(n); m = n << 1;
    for(Rint i = 1;i <= m;++ i){read(a[i].fi); read(a[i].se); id[i] = i;}
    sort(id + 1, id + m + 1, [&](int x, int y){return a[x] < a[y];});
    for(Rint i = 1;i <= m;++ i){
        int p = id[i];
        if(p <= n) S.insert(MP(a[p].se, p));
        else {
            auto it = S.lower_bound(MP(a[p].se, 1e9));
            if(it == S.begin()) EE(); -- it; mat[it->se] = p; S.erase(it);
        }
    }
    for(Rint i = 1;i <= n;++ i){
        int x1 = a[i].fi, x2 = a[mat[i]].fi, y1 = a[i].se, y2 = a[mat[i]].se;
        add[++t] = MP(y1, x1); del[t] = MP(y2, x1);
        if(x1 != x2){add[++t] = MP(y1, x2); del[t] = MP(y2, x2);}
        q[2*i-1] = MP(y1, MP(x1, x2)); q[2*i] = MP(y2, MP(x1, x2));
    }
    sort(q + 1, q + m + 1); sort(add + 1, add + t + 1); sort(del + 1, del + t + 1);
    int nowa = 1, nowd = 1;
    for(Rint i = 1;i <= m;++ i){
        while(nowd <= t && del[nowd].fi < q[i].fi) SS.erase(del[nowd++].se);
        while(nowa <= t && add[nowa].fi <= q[i].fi) if(!SS.insert(add[nowa++].se).se) EE();
        int l = q[i].se.fi, r = q[i].se.se;
        if(l != r && *SS.lower_bound(l+1) < r) EE();
    }
    for(Rint i = 1;i <= n;++ i) printf("%d\n", mat[i] - n);
}

ICPC World Finals 2014

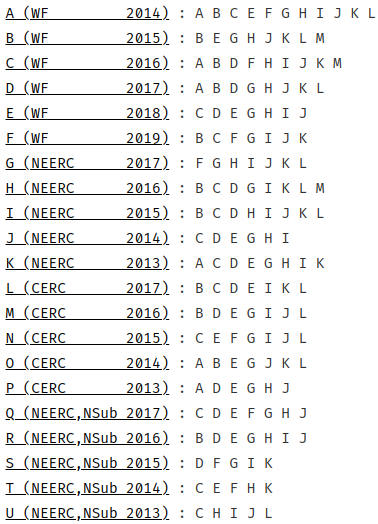
A Baggage

首先答案一定 \(\ge n\)，这是因为前 \(\lceil\frac n2\rceil\) 个 B 和后 \(\lceil\frac n2\rceil\) 个 A 都需要移动。现在考虑构造恰好 \(n\) 步的解。

暴搜 \(n\le 7\)，其中除了 \(n=3\) 之外只用到前 \(2\) 个空位置，然后将其他情况递归处理。

__BABABA....BABABA
ABBABABA....BAB__A
ABBA__BA....BABBAA
    [        ] <- 将这一部分递归处理（用到前两个空位置）
ABBAAAAA....__BBAA
A__AAAAA....BBBBAA
AAAAAAAA....BBBBBB

将 \(n>7\) 的情况用 \(4\) 步转化为 \(n-4\) 的子问题，又因为它达到了 \(n\) 步的下界，所以这个就是答案。

#include<bits/stdc++.h>
using namespace std;
int n;
void out(int a, int b){printf("%d to %d\n", a, b);}
void work(int l, int r){
    if(r-l == 5){out(2, -1); out(5, 2); out(3, -3); return;}
    if(r-l == 7){out(r-2, l-2); out(l+2, l+5); out(l-1, l+2); out(r-1, l-1); return;}
    if(r-l == 9){out(r-2, l-2); out(l+2, l+7); out(l+5, l+2); out(l-1, l+5); out(r-1, l-1); return;}
    if(r-l == 11){out(r-2, l-2); out(l+6, l+9); out(l+1, l+6); out(l+5, l+1); out(l-1, l+5); out(r-1, l-1); return;}
    if(r-l == 13){out(l+7, l-2); out(l+4, l+7); out(l+11, l+4); out(l+2, l+11); out(l+8, l+2); out(l-1, l+8); out(r-1, l-1); return;}
    out(r-2, l-2); out(l+2, r-2); work(l+4, r-4); out(l-1, r-5); out(r-1, l-1);
}
int main(){scanf("%d", &n); work(1, n<<1);}

K Surveillance

倍长为链，直接建树，每个点的父亲是覆盖这个点的所有线段中右端点的最大值 \(+1\)，枚举破环的位置 \(i\)，计算第一个 \(\ge i+n\) 的祖先与其的深度差。

#include<bits/stdc++.h>
using namespace std;
const int N = 2000003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, k, m, fa[21][N], dep[N], ans = 1e9;
int calc(int p){
    int u = p;
    for(int i = 20;~i;-- i)
        if(fa[i][p] < u + n) p = fa[i][p];
    p = fa[0][p]; if(p >= u + n) return dep[u] - dep[p]; return 1e9;
}
int main(){
    read(n); read(k); m = n<<1;
    for(int i = 1;i <= m+1;++ i) fa[0][i] = i;
    while(k --){
        int l, r; read(l); read(r);
        if(l <= r){chmax(fa[0][l], r+1); chmax(fa[0][l+n], r+n+1);}
        else chmax(fa[0][l], r+n+1);
    }
    for(int i = 2;i <= m;++ i) chmax(fa[0][i], fa[0][i-1]);
    for(int i = m-1;i;-- i) if(i < fa[0][i]) dep[i] = dep[fa[0][i]] + 1;
    for(int i = 1;i < 21;++ i)
        for(int j = 1;j <= m+1;++ j)
            fa[i][j] = fa[i-1][fa[i-1][j]];
    for(int i = 1;i <= n;++ i) chmin(ans, calc(i));
    if(ans > n) puts("impossible");
    else printf("%d\n", ans);
}

C Crane Balancing

物理题，直接模拟。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 103;
const double eps = 1e-10;
int n, x[N], y[N], L = 1e9, R; double ara, sum, ans1, ans2 = 1e18;
template<typename T>
void read(T &x){
    int ch = getchar(); bool f = false; x = 0;
    for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
    if(f) x = -x;
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int main(){
    read(n);
    for(Rint i = 1;i <= n;++ i){
        read(x[i]); read(y[i]);
        if(!y[i]){chmin(L, x[i]); chmax(R, x[i]);}
    }
    for(Rint i = 1;i <= n;++ i){
        int j = i % n + 1; LL tmp = x[i] * y[j] - x[j] * y[i];
        ara += tmp; sum += tmp * (x[i] + x[j]);
    } sum /= 6; ara /= 2; if(ara < 0){sum = -sum; ara = -ara;}
    if(L == x[1]){if(sum - L * ara < -eps) return puts("unstable"), 0;}
    else if(L > x[1]) chmin(ans2, (sum - L * ara) / (L - x[1]));
    else chmax(ans1, (sum - L * ara) / (L - x[1]));
    if(R == x[1]){if(sum - R * ara > eps) return puts("unstable"), 0;}
    else if(R > x[1]) chmax(ans1, (sum - R * ara) / (R - x[1]));
    else chmin(ans2, (sum - R * ara) / (R - x[1]));
    if(ans2 >= 1e18) printf("%d .. inf\n", (int) ans1);
    else if(ans1 <= ans2 + eps) printf("%d .. %d\n", (int) ans1, (int)(ans2 - eps) + 1);
    else puts("unstable");
}

G Metal Processing Plant

题目描述：给出 \(n\) 个点的无向完全图，定义直径为集合间最大边权。将其划分为两个点集，求直径之和的最小值。

数据范围：\(n\le 200\)。

two-pointer 枚举直径，转化为 2-sat 问题，暴力 Tarjan 判断，时间复杂度 \(O(m^2)\)。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 403, M = 80003;
int n, m, cnt, d[N][N], val[M], head[N], to[M], nxt[M], col[N], dfn[N], low[N], stk[N], tp, tim, cnum, ans;
bool ins[N];
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
inline bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
void dfs(int x){
    dfn[x] = low[x] = ++tim; stk[++tp] = x; ins[x] = true;
    for(Rint i = head[x];i;i = nxt[i])
        if(!dfn[to[i]]){dfs(to[i]); chmin(low[x], low[to[i]]);}
        else if(ins[to[i]]) chmin(low[x], dfn[to[i]]);
    if(low[x] == dfn[x]){int p; ++ cnum; do {p = stk[tp--]; col[p] = cnum; ins[p] = false;} while(p != x);}
}
bool check(int x, int y){
    if(val[x] + val[y] >= ans) return true;
    cnt = tp = cnum = tim = 0;
    memset(head, 0, sizeof head);
    memset(dfn, 0, sizeof dfn);
    memset(col, 0, sizeof col);
    for(Rint i = 0;i < n;++ i)
        for(Rint j = i+1;j < n;++ j){
            if(d[i][j] > x){add(i+n, j); add(j+n, i);}
            if(d[i][j] > y){add(i, j+n); add(j, i+n);}
        }
    for(Rint i = 0;i < (n<<1);++ i) if(!dfn[i]) dfs(i);
    for(Rint i = 0;i < n;++ i) if(col[i] == col[i+n]) return false;
    return true;
}
int main(){
    read(n);
    for(Rint i = 0;i < n;++ i)
        for(Rint j = i+1;j < n;++ j){
            read(d[i][j]); val[++m] = d[i][j];
        }
    sort(val + 1, val + m + 1); m = unique(val + 1, val + m + 1) - val; ans = val[m-1];
    for(Rint i = 0;i < n;++ i)
        for(Rint j = i+1;j < n;++ j)
            d[i][j] = lower_bound(val + 1, val + m, d[i][j]) - val;
    int u = m - 1;
    for(Rint x = 0;x < m;++ x) while(u >= x && check(x, u)){chmin(ans, val[x] + val[u]); -- u;}
    printf("%d\n", ans);
}

B Buffed Buffet

题目描述：给定正整数 \(w\) 和 \(d\) 份食物，食物有两种：离散的和连续的。离散食物 \((w_i,t_i,\Delta t_i)\) 表示一份食物有 \(w_i\text{ g}\) ，吃 \(n\) 份的价值为 \(nt_i-\binom n2\Delta t_i\)。连续食物 \((t_i,\Delta t_i)\) 表示吃 \(X\text{ g}\) 的价值为 \(Xt_i-\frac{X^2}2\Delta t_i\)。求吃 \(w\text{ g}\) 食物的最大价值。

数据范围：\(d\le 250,w\le 10^4,1\le w_i\le 10^4,0\le t_i,\Delta t_i\le 10^4\)。

分别考虑两种食物。对于离散食物，分别考虑相同 \(w_i\) 的食物，这些食物最多选 \(\lfloor\frac w{w_i}\rfloor\) 个，每次用堆找出最大价值的食物，做 01 背包，时间复杂度 \(O(w^2\log d)\)。对于连续食物，直接贪心，对于每个整数值 \(i\in[0,w]\)，二分出最后吃剩下的价值，计算价值和。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 253, M = 10003;
const double eps = 1e-11;
int n, w, m, pos; LL dp[M]; double ans = -1e20; pii con[M];
priority_queue<pii> dis[M];
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
double calc(double p){
    double res = 0;
    for(Rint i = 1;i <= m;++ i) res += max(con[i].fi - p, 0.) / con[i].se;
    return res;
}
int main(){
    scanf("%d%d", &n, &w);
    memset(dp, 0x80, sizeof dp); dp[0] = 0;
    for(Rint i = 1, ch, a, b, c;i <= n;++ i){
        for(ch = getchar();ch != 'D' && ch != 'C';ch = getchar());
        if(ch == 'D'){
            scanf("%d%d%d", &a, &b, &c);
            dis[a].push(MP(b, c));
        } else {
            scanf("%d%d", &b, &c);
            con[++m] = MP(b, c);
        }
    }
    for(Rint i = 1;i <= w;++ i) if(!dis[i].empty()){
        int k = w / i;
        while(k --){
            pii now = dis[i].top(); dis[i].pop(); pos = min(w, pos + i);
            for(Rint j = pos;j >= i;-- j) chmax(dp[j], dp[j - i] + now.fi);
            now.fi -= now.se; dis[i].push(now);
        }
    }
    if(!m){if(dp[w] <= -1e18) puts("impossible"); else printf("%lld\n", dp[w]); return 0;}
    double l = -1e18, r = 10000, mid, tmp;
    for(Rint i = 0;i <= w;++ i, r = 10000) if(dp[w-i] > -1e18){
        while(r - l > eps) if(calc(mid = (l + r) / 2) > i) l = mid; else r = mid;
        tmp = 0; for(Rint i = 1;i <= m;++ i) if(con[i].fi >= l) tmp += (con[i].fi + l) * (con[i].fi - l) / con[i].se;
        chmax(ans, dp[w-i] + tmp / 2);
    }
    if(ans <= -1e18) puts("impossible");
    else printf("%.9lf\n", ans);
}

H Pachinko

题目描述：给定 \(w\times h\) 的矩阵，每个元素是.XT（弹簧、障碍、终点）和四个实数 \(u,d,l,r\)，若你当前在.上，你会以 \(u,d,l,r\) 的概率随机向四个方向走，若该方向有障碍或边界则重新随机。对于每个T，求最终到达它的概率。

数据范围：\(w\le 20,2\le h\le 10^4,u+d+l+r=1\)。

求每个点的期望访问次数可以解方程。

因为有 \(0\) 系数的存在所以不能用主元法，需要用带状矩阵消元。时间复杂度 \(O(w^3h)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 23, M = 10003; const double eps = 1e-11;
int sgn(double x){return (x < -eps) ? -1 : (x > eps);}
int n, m, tmp; double u, d, l, r, uc[M][N], dc[M][N], lc[M][N], rc[M][N];
char s[M][N];
struct Node {
    double c[3][N], v;
} f[M][N];
int main(){
    scanf("%d%d%lf%lf%lf%lf", &m, &n, &u, &d, &l, &r); u /= 100; d /= 100; l /= 100; r /= 100;
    for(Rint i = 1;i <= n;++ i) scanf("%s", s[i] + 1);
    for(Rint i = 1;i <= m;++ i) if(s[1][i] == '.') ++ tmp;
    for(Rint i = 1;i <= m;++ i) if(s[1][i] == '.') f[1][i].v = 1./tmp;
    for(Rint i = 0;i <= n+1;++ i) s[i][0] = s[i][m+1] = 'X';
    for(Rint i = 0;i <= m+1;++ i) s[0][i] = s[n+1][i] = 'X';
    for(Rint i = 1;i <= n;++ i)
        for(Rint j = 1;j <= m;++ j) if(s[i][j] == '.'){
            double tmp = 0;
            if(s[i-1][j] != 'X'){uc[i][j] = u; tmp += u;}
            if(s[i][j-1] != 'X'){lc[i][j] = l; tmp += l;}
            if(s[i][j+1] != 'X'){rc[i][j] = r; tmp += r;}
            if(s[i+1][j] != 'X'){dc[i][j] = d; tmp += d;}
            if(sgn(tmp)){uc[i][j] /= tmp; lc[i][j] /= tmp; rc[i][j] /= tmp; dc[i][j] /= tmp;}
        }
    for(Rint i = 1;i <= n;++ i)
        for(Rint j = 1;j <= m;++ j) if(s[i][j] != 'X'){
            f[i][j].c[1][j] = 1; f[i][j].c[0][j] = -dc[i-1][j]; f[i][j].c[2][j] = -uc[i+1][j]; f[i][j].c[1][j-1] = -rc[i][j-1]; f[i][j].c[1][j+1] = -lc[i][j+1];
        }
    for(Rint i = 1;i <= n;++ i)
        for(Rint j = 1;j <= m;++ j) if(s[i][j] != 'X'){
            if(!sgn(f[i][j].c[1][j])) continue;
            double tmp = f[i][j].c[1][j];
            for(Rint k = j;k <= m;++ k) f[i][j].c[1][k] /= tmp;
            for(Rint k = 1;k <= j;++ k) f[i][j].c[2][k] /= tmp;
            f[i][j].v /= tmp;
            for(Rint k = j + 1;k <= m;++ k){
                tmp = f[i][k].c[1][j];
                if(sgn(tmp)){
                    for(Rint l = j;l <= m;++ l) f[i][k].c[1][l] -= f[i][j].c[1][l] * tmp;
                    for(Rint l = 1;l <= j;++ l) f[i][k].c[2][l] -= f[i][j].c[2][l] * tmp;
                    f[i][k].v -= f[i][j].v * tmp;
                }
            }
            for(Rint k = 1;k <= j;++ k){
                tmp = f[i+1][k].c[0][j];
                if(sgn(tmp)){
                    for(Rint l = j;l <= m;++ l) f[i+1][k].c[0][l] -= f[i][j].c[1][l] * tmp;
                    for(Rint l = 1;l <= j;++ l) f[i+1][k].c[1][l] -= f[i][j].c[2][l] * tmp;
                    f[i+1][k].v -= f[i][j].v * tmp;
                }
            }
        }
    for(Rint i = n;i;-- i)
        for(Rint j = m;j;-- j) if(s[i][j] != 'X'){
            if(!sgn(f[i][j].c[1][j])) continue;
            double tmp = f[i][j].v /= f[i][j].c[1][j];
            for(Rint k = 1;k < j;++ k) f[i][k].v -= tmp * f[i][k].c[1][j];
            for(Rint k = j;k <= m;++ k) f[i-1][k].v -= tmp * f[i-1][k].c[2][j];
        }
    for(Rint i = 1;i <= n;++ i)
        for(Rint j = 1;j <= m;++ j) if(s[i][j] == 'T')
            printf("%.9lf\n", f[i][j].v);
}

2015-2016 ACM-ICPC Northeastern European Regional Contest (NEERC 15)

J Jump

题目描述：给定正整数 \(n\)，交互器有一个长为 \(n\) 的字符串 \(S\)，每次可以询问长为 \(n\) 的字符串 \(T\)，若 \(S=T\) 则直接结束，否则你可以知道 \(S\) 与 \(T\) 是否恰好有 \(\frac{n}{2}\) 个字符相同。要求在 \(n+500\) 次操作内结束。

数据范围：\(n\le 10^3\)，\(n\) 为偶数。

先随机到有恰好 \(\frac n2\) 个字符相同的字符串，然后每次修改 \(T_1,T_i\) 可以得到 \(T_1\) 与 \(T_i\) 是否应同时反转，再询问两次即可。根据斯特林近似，操作次数为 \(n+\sqrt{2\pi n}+O(1)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 1003;
int n, m; bool a[N], b[N];
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
void guess(){for(Rint i = 1;i <= n;++ i) a[i] = rng() & 1;}
void out(){for(Rint i = 1;i <= n;++ i) printf("%d", a[i]); putchar('\n'); fflush(stdout); scanf("%d", &m); if(m == n) exit(0);}
void work(){
    a[1] ^= 1;
    for(Rint i = 2;i <= n;++ i){
        a[i] ^= 1; out(); b[i] = m; a[i] ^= 1;
    } a[1] ^= 1;
    for(Rint i = 2;i <= n;++ i) if(b[i]) a[i] ^= 1; out();
    for(Rint i = 1;i <= n;++ i) a[i] ^= 1; out();
}
int main(){
    scanf("%d", &n);
    while(true){guess(); out(); if(m) work();}
}

2013-2014 ACM-ICPC, NEERC, Northern Subregional Contest

C Correcting Curiosity

直接枚举 \(A\)，计算出出现次数就可以得到 \(B\) 的长度，进而得到 \(B\)。

使用字符串 hash 判断相等，时间复杂度 \(O(n^2+m)\)。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
#define PB push_back
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 2003, X = 20201018, mod = 1004535809;
int n, m, h1[N], h2[N], pw[N], nxt[N], ans1, ans2, l = 1;
char s1[N], s2[N];
bool vis[N];
int calc(int *h, int l, int r){return (h[r] - (LL) h[l-1] * pw[r-l+1] % mod + mod) % mod;}
unordered_map<int, int> M, S;
int main(){
    freopen("curiosity.in", "r", stdin);
    freopen("curiosity.out", "w", stdout);
	gets(s1+1); ans1 = n = strlen(s1+1); gets(s2+1); ans2 = m = strlen(s2+1); pw[0] = 1;
	for(Rint i = 1;i <= n;++ i) h1[i] = ((LL) X * h1[i-1] + s1[i]) % mod;
	for(Rint i = 1;i <= m;++ i) h2[i] = ((LL) X * h2[i-1] + s2[i]) % mod;
	for(Rint i = 1;i <= n || i <= m;++ i) pw[i] = (LL) pw[i-1] * X % mod;
	for(Rint len = 1;len < n;++ len){
		M.clear(); S.clear();
		memset(nxt, 0, sizeof nxt);
		memset(vis, 0, sizeof vis);
		for(Rint i = n-len+1;i;-- i){
			if(i+2*len-1 <= n) M[calc(h1, i+len, i+2*len-1)] = i+len;
			int tmp = calc(h1, i, i+len-1);
			if(M.count(tmp)) nxt[i] = M[tmp];
			if(S.count(tmp)) vis[S[tmp]] = true;
			S[tmp] = i;
		}
		for(Rint i = 1;i <= n-len+1;++ i) if(!vis[i]){
			int t1 = 0, now = i;
			while(now){++ t1; now = nxt[now];}
			int t2 = n - t1 * len, len2 = (m - t2) / t1;
			if(m < t2 || len + len2 >= ans1 + ans2 || (m - t2) % t1) continue;
			int lst = 1; now = i; t1 = 0; t2 = calc(h2, i, i+len2-1);
			while(now){
				t1 = ((LL) t1 * pw[now - lst] + calc(h1, lst, now - 1)) % mod;
				t1 = ((LL) t1 * pw[len2] + t2) % mod; lst = now + len; now = nxt[now];
			} t1 = ((LL) t1 * pw[n - lst + 1] + calc(h1, lst, n)) % mod;
			if(t1 == h2[m]){l = i; ans1 = len; ans2 = len2;}
		}
	}
	printf("s/");
	for(Rint i = l;i < l + ans1;++ i) putchar(s1[i]); putchar('/');
	for(Rint i = l;i < l + ans2;++ i) putchar(s2[i]); puts("/g");
}

H Heavy Chain Clusterization

题目可以转化为求给定两组集合，组内集合不交，求最小覆盖。

将集合设为点，元素设为边，转化为二分图最小点覆盖。使用 dinic 计算，左部分中有流的点即为选中的集合，进而推出右部分选了哪些集合。时间复杂度 \(O(\sum |s_i|+n\sqrt n)\)。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
#define PB push_back
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 10003, M = N * 3;
template<typename T>
void read(T &x){
	int ch = getchar(); x = 0; bool f = false;
	for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
	for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
	if(f) x = -x;
}
int n, k, m1, m2, a[N], b[N], head[N], to[M], nxt[M], w[M], S, T, dep[N], cur[N], q[N], f, r, ans;
char str[N];
map<string, int> ma, mb;
vector<int> vec[N];
void add(int a, int b, int c){
	static int cnt = 1;
	to[++ cnt] = b; nxt[cnt] = head[a]; head[a] = cnt; w[cnt] = c;
	to[++ cnt] = a; nxt[cnt] = head[b]; head[b] = cnt; w[cnt] = 0;
}
bool bfs(){
	memset(dep, -1, sizeof dep); memcpy(cur, head, sizeof cur);
	f = r = 0; q[r++] = S; dep[S] = 0;
	while(f < r){
		int u = q[f++];
		for(Rint i = head[u];i;i = nxt[i])
			if(!~dep[to[i]] && w[i]){dep[to[i]] = dep[u] + 1; q[r++] = to[i];}
	}
	return ~dep[T];
}
int dfs(int x, int lim){
	if(x == T || !lim) return lim;
	int flow = 0, f;
	for(Rint &i = cur[x];i;i = nxt[i])
		if(dep[to[i]] == dep[x] + 1 && (f = dfs(to[i], min(lim, w[i])))){
			lim -= f; flow += f; w[i] -= f; w[i^1] += f;
		}
	return flow;
}
int main(){
	freopen("heavy.in", "r", stdin);
	freopen("heavy.out", "w", stdout);
	read(n); read(k);
	for(Rint i = 1;i <= n;++ i){
		string s, tmp; scanf("%s", str); s = str;
		tmp = s.substr(0, k); if(!ma.count(tmp)) ma[tmp] = ++m1; a[i] = ma[tmp];
		tmp = s.substr(s.size() - k, k); if(!mb.count(tmp)) mb[tmp] = ++m2; b[i] = mb[tmp];
	}
	S = m1 + m2 + 1; T = S + 1;
	for(Rint i = 1;i <= m1;++ i) add(S, i, 1);
	for(Rint i = 1;i <= m2;++ i) add(i + m1, T, 1);
	for(Rint i = 1;i <= n;++ i) add(a[i], m1 + b[i], 1);
	while(bfs()) ans += dfs(S, 1e9); printf("%d\n", ans);
	for(Rint i = 1;i <= n;++ i) if(!~dep[a[i]]) vec[a[i]].PB(i); else vec[m1 + b[i]].PB(i);
	for(Rint i = 1;i <= m1 + m2;++ i) if(!vec[i].empty()){
		printf("%llu", vec[i].size());
		for(Rint u : vec[i]) printf(" %d", u);
		putchar('\n');
	}
}

J J

题目所述的 Complexity 即为 \(X\) 的次数，维护 \(X\) 的多项式然后暴力计算即可。

不想模拟了aaa

2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17)

G The Great Wall

题目描述：给定正整数 \(n,r,k\) 和三个长为 \(n\) 的正整数序列 \(a_0,a_1,a_2\)，定义

\[w(x,y)=\sum_{i=1}^na_{[i\in(x-r,x]]+[i\in(y-r,y]],i} \]

其中 \(r\le x<y\le n\)。求这 \(\binom{n-r+1}2\) 个值中的第 \(k\) 小。

数据范围：\(n\le 30000,r<n,k\le\binom{n-r+1}2,1\le a_{0,i}<a_{1,i}<a_{2,i}\le 10^6\)。

将 \(a_{?,i}\) 作差分，设 \(sum=\sum a_{0,i},s_{1,i}=\sum_{j=1}^ia_{1,j},s_{2,i}=\sum_{j=1}^ia_{2,j}\)。

  • 若 \(x<y\le x+r\)，则答案为 \(sum+(s_{2,x}-s_{1,x-r})+(s_{1,y}-s_{2,y-r})\)。
  • 若 \(y>x+r\)，则答案为 \(sum+(s_{1,x}-s_{1,x-r})+(s_{1,y}-s_{1,y-r})\)。

二分答案，用 two-pointer 配合树状数组维护，时间复杂度 \(O(n\log n\log V)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 30005;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, r, m, p[N], q[N], t[N], tr[N]; LL sum, k, f[N], g[N], h[N], a[3][N];
void upd(int p){for(;p <= n;p += p & -p) ++ tr[p];}
int qry(int p){int res = 0; for(;p;p -= p & -p) res += tr[p]; return res;}
LL calc(LL val){
    memset(tr + 1, 0, n << 2); int now = 1; LL res = 0;
    for(Rint i = m;i;-- i){
        while(now <= m && f[p[i]] + g[q[now]] <= val) upd(q[now++]);
        res += qry(p[i] + r - 1) - qry(p[i]);
    } memset(tr + 1, 0, n << 2); now = 1;
    for(Rint i = m;i;-- i){
        while(now <= m && h[t[i]] + h[t[now]] <= val) upd(t[now++]);
        res += qry(n) - qry(t[i] + r - 1);
    } return res;
}
int main(){
    read(n); read(r); read(k); m = n - r + 1;
    for(Rint i = 1;i <= n;++ i) read(a[0][i]);
    for(Rint i = 1;i <= n;++ i) read(a[1][i]);
    for(Rint i = 1;i <= n;++ i){read(a[2][i]); a[2][i] -= a[1][i]; a[1][i] -= a[0][i];}
    for(Rint i = 1;i <= n;++ i){sum += a[0][i]; a[1][i] += a[1][i-1]; a[2][i] += a[2][i-1];}
    for(Rint i = 1;i <= m;++ i){f[i] = a[2][i+r-1] - a[1][i-1]; g[i] = a[1][i+r-1] - a[2][i-1]; h[i] = a[1][i+r-1] - a[1][i-1]; p[i] = q[i] = t[i] = i;}
    sort(p + 1, p + m + 1, [&](int x, int y){return f[x] < f[y];});
    sort(q + 1, q + m + 1, [&](int x, int y){return g[x] < g[y];});
    sort(t + 1, t + m + 1, [&](int x, int y){return h[x] < h[y];});
    LL L = 0, R = a[2][n] + a[1][n], mid;
    while(L < R){
        mid = L + R >> 1;
        if(calc(mid) < k) L = mid + 1; else R = mid;
    } printf("%lld\n", sum + L);
}

H Hack

这是一道交互题

题目描述：给定伪代码

modPow(a, d, n) {
	r = 1;
	for (i = 0; i < 60; ++i) {
		if ((d & (1 << i)) != 0) {
			r = r * a % n;
		}
		a = a * a % n;
	}
}

其中计算 \(x\times y\bmod n\) 的时间为 \((\lfloor\log_2x\rfloor+2)(\lfloor\log_2y\rfloor+2)\)，其他步骤的计算时间忽略不计。

给定正整数 \(n\)，交互器有正整数 \(d\)，每次询问自然数 \(a<n\)，交互器返回计算 \(\text{modPow}(a,d,n)\) 的时间。求 \(d\)。

数据范围：\(n=pq\)，\(p,q\) 为 \((2^{29},2^{30})\) 中的随机质数。设 \(m=(p-1)(q-1)\)，则 \(d\) 为 \(\{k|k\in\N_+,k<m,k\bot m\}\) 中的随机整数，询问次数 \(\le 3\times 10^4\)，数据组数 \(=30\)，时间限制 \(10\) s。

首先平方部分是固定的，可以去掉它。

做法太神仙，直接上正解。随机 \(3\times 10^4\) 个 \(a\) 弄上去，易得 \(d\) 的第 \(0\) 位为 \(1\)，之后从低到高计算 \(d\) 的每一位。以第 \(1\) 位为例，设 \(p_i\) 为当前位中代码第 \(5\) 行的计算时间（若 if 中的条件成立），\(q_i\) 为总计算时间，计算 \(p\) 与 \(q\) 的取样协方差

\[\text{Cov}(p,q)=\text E[pq]-\text E[p]\text E[q] \]

若当前位为 \(1\)，则 \(p_i\) 为 \(a_i\times a_i^2\) 的计算时间，\(q_i\) 中与 \(p_i\) 关系密切的只有 \(a_i\times a_i^2\) 的部分，因此 \(\text{Cov}(p,q)\) 近似于 \(\text{Cov}(p,p)=\text{Var}(p)\)。

若当前位为 \(0\)，则 \(p_i\) 为 \(a_i\times a_i^2\) 的计算时间，\(q_i\) 中与 \(p_i\) 关系密切的只有下一步的计算时间，因此 \(\text{Cov}(p,q)\) 近似于 \(\text{Cov}(p,t)\)，其中 \(t\) 为 \(a_i\times a_i^4\) 的计算时间。

比较一下哪个离得更近就是哪个（？

现在考虑定量计算这个方法的正确性...个鬼啊，不会证啊啊啊啊...

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
typedef long double LD;
const int N = 30000;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int bit(LL x){return x ? 65 - __builtin_clzll(x) : 1;}
LL get(LL x, LL y){return bit(x) * bit(y);}
LD cov(LL *x, LL *y){
    LD sum1 = 0, sum2 = 0, sum3 = 0;
    for(Rint i = 0;i < N;++ i){sum1 += x[i] * y[i]; sum2 += x[i]; sum3 += y[i];}
    return sum1 / N - sum2 * sum3 / N / N;
}
LL n, ans = 1, a[N], p[N], q[N], d[N], pw[N];
LL mul(LL a, LL b){
    a %= n; b %= n;
    LL res = a * b - ((LL)((LD) a / n * b + 0.5) * n);
    return res < 0 ? res + n : res;
}
int main(){
    read(n);
    for(Rint i = 0;i < N;++ i){
        a[i] = rng() % (n - 1) + 1;
        printf("? %lld\n", a[i]); fflush(stdout); read(q[i]);
        pw[i] = mul(a[i], a[i]); q[i] -= get(1, a[i]);
        LL tmp = a[i];
        for(Rint j = 0;j < 60;++ j){
            q[i] -= get(tmp, tmp);
            tmp = mul(tmp, tmp);
        }
    }
    for(Rint i = 1;i < 60;++ i){
        for(Rint j = 0;j < N;++ j){p[j] = get(a[j], pw[j]); d[j] = get(a[j], mul(pw[j], pw[j]));}
        LD A = cov(p, q), B = cov(p, p), C = cov(p, d);
        if(abs(A - B) < abs(A - C)){
            ans |= 1ll << i;
            for(Rint j = 0;j < N;++ j){a[j] = mul(a[j], pw[j]); q[j] -= p[j];}
        }
        for(Rint j = 0;j < N;++ j) pw[j] = mul(pw[j], pw[j]);
    }
    printf("! %lld\n", ans);
}

I Interactive Sort

这是一道交互题

题目描述：给定正整数 \(n\)，交互器有两个序列 \(e,o\)，分别表示 \([1,n]\) 中偶数和奇数的排列。每次询问 \((i,j)\) 交互器返回 \(e_i\) 与 \(o_j\) 的大小关系。求 \(e,o\)。

数据范围：\(n\le 10^4\)，询问次数 \(\le 3\times 10^5\)，数据随机。

用 \(e\) 将 \(o\) 分割成值域上升的序列，期望询问次数 \(O(n\log n)\)。

#include<bits/stdc++.h>
#define Rint register int
#define PB push_back
using namespace std;
typedef vector<int> vi;
const int N = 10003;
int n, n0, n1, cnt, pr[2][N]; vi p[N], t[2]; unordered_map<int, bool> M;
bool qry(int x, int y){
    int tmp = (x - 1) * n1 + y; if(M.count(tmp)) return M[tmp];
    printf("? %d %d\n", x, y); fflush(stdout);
    char ch[4]; scanf("%s", ch); return M[tmp] = ch[0] == '<';
}
bool work(int x, int k){
    t[0].clear(); t[1].clear();
    for(Rint i : p[k]) t[qry(x, i)].PB(i);
    return !(t[0].empty() || t[1].empty());
}
int main(){
    scanf("%d", &n); n0 = n >> 1; n1 = n - n0; cnt = 1;
    for(Rint i = 1;i <= n1;++ i) p[1].PB(i);
    for(Rint i = 1;i <= n0;++ i){
        int l = 1, r = cnt, mid;
        while(l < r){
            mid = l + r + 1 >> 1;
            if(qry(i, p[mid][0])) r = mid - 1; else l = mid;
        }
        if(l > 1 && work(i, l - 1)) -- l;
        else if(l < cnt && work(i, l + 1)) ++ l;
        else if(!work(i, l)){pr[0][i] = n0; continue;}
        for(Rint j = ++cnt;j > l+1;-- j) p[j] = p[j-1];
        p[l] = t[0]; p[l+1] = t[1];
        for(Rint j = 1;j <= l;++ j) pr[0][i] += p[j].size();
    }
    for(Rint i = 1;i <= cnt;++ i) pr[1][p[i][0]] = i;
    putchar('!');
    for(Rint i = 1;i <= n0;++ i) printf(" %d", pr[0][i] << 1);
    for(Rint i = 1;i <= n1;++ i) printf(" %d", (pr[1][i] << 1) - 1);
    putchar('\n');
}

K Knapsack Cryptosystem

题目描述：给定 \(n\) 个正整数 \(b_i\) 和正整数 \(s,q\)，求长为 \(n\) 的 \(01\) 串 \(S\) 使 \(s\equiv \sum b_iS_i(\text{mod }q)\)。

数据范围：\(n\le 64,q=2^{64},b_i<q,s<q\)，存在 \(n\) 个正整数 \(a_i\) 和正整数 \(r\) 满足 \(a_i>\sum_{j=1}^{i-1}a_j,q>\sum_{i=1}^na_i\)，\(r\) 是奇数，\(b_i=a_ir\bmod q\)，保证有解。

\(n\le 42\) 时直接暴力。\(n>42\) 时，因为 \(a_1<2^{22}\)，并且 \(\text{lowbit}(a_i)=\text{lowbit}(b_i)\)，设为 \(k\)。所以可以直接求出 \(r^{-1}\) 的后 \(64-k\) 位，更高的 \(k\) 位直接暴力枚举。时间复杂度 \(O(\sqrt[3]q\log q)\)。

#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef unsigned long long LL;
typedef pair<LL, LL> pii;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
const int N = 64, M = 1 << 21;
int n, m, k, n1, n2; LL b[N], s; pii t[2][M];
LL get(LL x){LL res = 0; for(int i = 0;i < n;++ i, x >>= 1) if(x & 1) res += b[i]; return res;}
void GG(LL x){for(int i = 0;i < n;++ i, x >>= 1) putchar((x & 1) + '0'); exit(0);}
int main(){
    read(n); for(int i = 0;i < n;++ i) read(b[i]); read(s);
    if(n <= 42){
        m = n >> 1; n1 = 1 << m; n2 = 1 << n - m;
        for(int i = 0;i < n1;++ i) t[0][i] = MP(get(i), i);
        for(int i = 0;i < n2;++ i) t[1][i] = MP(s - get((LL)i<<m), (LL)i<<m);
        sort(t[0], t[0] + n1); sort(t[1], t[1] + n2);
        int p1 = 0, p2 = 0;
        while(p1 < n1 && p2 < n2)
            if(t[0][p1].fi == t[1][p2].fi) GG(t[0][p1].se | t[1][p2].se);
            else if(t[0][p1].fi < t[1][p2].fi) ++ p1; else ++ p2;
    } else {
        k = __builtin_ctzll(b[0]); LL S = b[0] >> k, Si = 1; n1 = 1ull << 66 - n - k; n2 = 1ull << k;
        for(int i = 1;i < 64;++ i) if(S * Si >> i & 1) Si |= 1ull << i;
        for(int i = 1;i < n1;i += 2)
            for(int j = 0;j < n2;++ j){
                LL r = Si * i + ((LL)j << 64 - k), tt = s * r, ans = 0;
                for(int _ = n-1;~_;-- _){
                    LL tmp = b[_] * r;
                    if(tt >= tmp){tt -= tmp; ans |= 1ull << _;}
                    if(tt >= tmp) break;
                } if(!tt) GG(ans);
            }
    }
}

L Laminar Family

题目描述：给定 \(n\) 个点的树和 \(m\) 条链 \((a_i,b_i)\)，问是否存在两条链相交且不包含。

数据范围：\(n,m\le 10^5\)。

按照链长从大到小染色，判断是否全相等。树剖+线段树，时间复杂度 \(O((n+m)\log^2n)\)。

2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest

D Dividing Marbles

题目描述：给定有 \(n\) 个的一堆石子，每次操作将一堆石子分割，并按石子个数将各堆石子去重，问最终到达一堆 \(1\) 个石子的状态的最少步数的一种方案。\(t\) 组数据。

数据范围：\(t\le 500\)，\(\exist d_1,d_2,d_3,d_4\in[0,20]\cap\N,n=2^{d_1}+2^{d_2}+2^{d_3}+2^{d_4}\)。

容易找到 \(\lfloor\log_2 n\rfloor+\text{popcount}(n)-1\) 步的方案。题解说 \(\text{popcount}(n)\le 8\) 时不可能优于 \(\lfloor\log_2n\rfloor+\lceil\log_2\text{popcount}(n)\rceil\)，所以只用考虑 \(\text{popcount}(n)=4\)。

直接暴搜即可。

C Consonant Fencity

直接暴力即可...签到题咋混进来了...

E Equal Numbers

题目描述：给定 \(n\) 个正整数 \(a_i\)，一次操作选定一个 \(a_i\)，将其乘以任意一个正整数。\(\forall 0\le k\le n\)，求出 \(k\) 次操作后 \(a_i\) 中不同数个数的最小值。

数据范围：\(n\le 3\times 10^5,a_i\le 10^6\)。

考虑最优解实际上就只能是将 \(k\) 个 \(a_i\) 变为它们的公倍数，对这个公倍数是否在序列中进行分类讨论即可，时间复杂度 \(O(V\log V)\)。

#include<bits/stdc++.h>
#define PB push_back
using namespace std;
const int N = 1000003, M = 300003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
vector<int> v;
int n, m, tot, c[N], ans[M]; bool vis[N];
int main(){
    freopen("equal.in", "r", stdin); freopen("equal.out", "w", stdout); read(n);
    for(int i = 1, x;i <= n;++ i){read(x); ++ c[x]; chmax(m, x);}
    for(int i = 1;i <= m;++ i) if(c[i]){++ tot; for(int j = (i<<1);j <= m && !vis[i];j += i) if(c[j]) vis[i] = true;}
    for(int i = 1;i <= m;++ i) if(vis[i]) v.PB(c[i]);
    for(int i = 0;i <= n;++ i) ans[i] = tot; sort(v.begin(), v.end());
    for(int i = 0, sum = 0;i < v.size();++ i) chmin(ans[sum += v[i]], tot - i - 1);
    for(int i = 1;i <= m;++ i) if(c[i] && !vis[i]) v.PB(c[i]); sort(v.begin(), v.end());
    for(int i = 0, sum = 0;i < v.size();++ i) chmin(ans[sum += v[i]], tot - i);
    for(int i = 1;i <= n;++ i) chmin(ans[i], ans[i-1]);
    for(int i = 0;i <= n;++ i) printf("%d ", ans[i]);
}

2015 ACM-ICPC World Finals

L Weather Report

题目描述：给定 \(p_0,p_1,p_2,p_3\) 和正整数 \(n\)，表示在长度为 \(n\)，字符集为 \(\{0,1,2,3\}\) 的所有字符串中，第 \(i\) 个字符是 \(j\) 的概率为 \(p_j\)。求将这 \(4^n\) 个字符串进行 Huffman 编码时的期望位数。

数据范围：\(n\le 20,\sum p_i=1,p_i\ge 0\)，绝对或相对误差 \(\le 10^{-4}\)。

将相同概率的字符串合并再做合并果子。时间复杂度 \(O(n^4\log^2n)\)。

#include<bits/stdc++.h>
#define fi first
#define se second
#define MP make_pair
using namespace std;
typedef long long LL;
typedef pair<double, LL> pii;
priority_queue<pii, vector<pii>, greater<pii> > pq;
int n; double p[4][21], ans; LL fac[21];
int main(){
    scanf("%d%lf%lf%lf%lf", &n, p[0]+1, p[1]+1, p[2]+1, p[3]+1);
    p[0][0] = p[1][0] = p[2][0] = p[3][0] = fac[0] = 1;
    for(int i = 1;i <= n;++ i) fac[i] = i * fac[i-1];
    for(int i = 0;i < 4;++ i)
        for(int j = 2;j <= n;++ j) p[i][j] = p[i][j-1] * p[i][1];
    for(int i = 0;i <= n;++ i)
        for(int j = 0;j <= n-i;++ j)
            for(int k = 0;k <= n-i-j;++ k)
                pq.push(MP(p[0][i]*p[1][j]*p[2][k]*p[3][n-i-j-k], fac[n]/fac[i]/fac[j]/fac[k]/fac[n-i-j-k]));
    while(pq.size() > 1){
        pii now = pq.top(); pq.pop();
        if(now.se > 1){ans += (now.se>>1)*now.fi*2; pq.push(MP(now.fi*2, now.se>>1)); if(now.se & 1) now.se = 1; else continue;}
        pii tmp = pq.top(); pq.pop();
        ans += now.fi + tmp.fi; pq.push(MP(now.fi + tmp.fi, 1)); if(tmp.se > 1) pq.push(MP(tmp.fi, tmp.se - 1));
    } printf("%.6lf\n", ans);
}

H Qanat

设 \(f_i(x)\) 表示挖 \(i\) 条沟渠，\(w=x\) 时的答案（斜率为 \(k\)）。

\[\begin{aligned} f_0(x)&=(\frac{k+1}2)^2x^2\\ f_i(x)&=a_ix^2+b_ix+c_i \\ f_{i+1}(x)&=\min_{0<y<x}\{f_i(y)+\frac12((k+1)x+(k-1)y)^2-(ky)^2\} \\ &=\min_{0<y<x}\{\Big(a_i+1-\frac12(k+1)^2\Big)y^2+\Big(b_i+(k^2-1)x\Big)y+c_i+\frac12(k+1)^2x^2\} \\ &=\frac12(k+1)^2x^2+c_i+\frac{(b_i+(k^2-1)x)^2}{2k^2+4k-4a_i-2}&, y=\frac{b_i+(k^2-1)x}{k^2+2k-2a_i-1} \end{aligned} \]

因为沟渠挖在两边都是不优的，所以对称轴一定 \(\in (0,x)\)。

解二次函数最值即可。

E Evolution in Parallel

将所有字符串按长度从大到小排序，显然有解则一条链的长度区间包含另一条，直接贪心连边即可。

2016 ACM-ICPC World Finals

A Balanced Diet

设 \(A=\sum a\)，发现 \(nf_i-1<s_i<nf_i+1\) 当且仅当 \(\lfloor nf_i\rfloor\le s_i\le\lceil nf_i\rceil\)。也就是当 \(n=A\) 时 \(s_i\) 已经确定，所以当 \(k\ge\sum a\) 时将 \(k:=k\bmod(\sum a)\)。

此时，只要能够吃到 \(\sum a\) 天就说明 forever。

发现 \(s_i\) 的这个限制就相当于固定了第 \(j\) 个 \(i\) 属于哪个区间，这事一个经典贪心，时间复杂度 \(O(A\log A)\)。

#include<bits/stdc++.h>
#define Rint register int
#define MP make_pair
#define fi first
#define se second
#define PB push_back
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0; bool f = false;
    for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
    if(f) x = -x;
}
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
inline bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int m, k, suma, a[N], b[N], tt[N], tot, now; pii p[N]; priority_queue<int, vector<int>, greater<int> > pq;
int main(){
    read(m); read(k);
    for(int i = 1;i <= m;++ i){read(a[i]); suma += a[i];}
    for(int i = 1;i <= k;++ i) read(b[i % suma]); k %= suma;
    for(int i = 1;i <= k;++ i) ++ tt[b[i]];
    for(int i = 1;i <= m;++ i)
        for(int j = tt[i]+1;j <= a[i];++ j)
            p[tot++] = MP(suma * (j - 1ll) / a[i], ((LL)suma * j - 1) / a[i]);
    sort(p, p + tot);
    for(int i = k;i < suma;++ i){
        while(now < tot && p[now].fi <= i) pq.push(p[now++].se);
        if(pq.empty() || pq.top() < i) return printf("%d\n", i-k-1), 0; pq.pop();
    } puts("forever");
}

B Branch Assignment

先跑两次最短路计算 \(\text{dis}(b+1,i)\) 和 \(\text{dis}(i,b+1)\)，问题就可以转化为将可重集合 \(A=\{\text{dis}(b+1,i)+\text{dis}(i,b+1)|1\le i\le b\}\) 分为 \(s\) 个非空的集合，一个集合的代价为 \(f(S)=(|S|-1)\text{sum}(S)\)，求代价之和最小值。

易得将 \(A\) 排序之后每个集合都是一个连续区间，且区间长度单调递减，设 \(dp_{i,j}\) 表示前 \(j\) 个数组成 \(i\) 个集合的代价之和最小值，\(s_i\) 表示前缀和，则

\[dp_{i,j}=\min_{k=j-\lfloor\frac ji\rfloor}^{j-1}(dp_{i-1,k}+(j-k-1)(s_j-s_k)) \]

时间复杂度 \(O(r\log n+bs\log b)\)。

K String Theory

人被玩傻了...

当 \(k\ge 1\) 时，一堆 \(k\)-quotation 可以合成一个。所以 \(k>1\) 时直接暴力判断，\(k=1\) 时即为 \(sum=2\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 103;
int n, a[N], tmp[N], sum;
int main(){
    scanf("%d", &n);
    for(int i = 1;i <= n;++ i){scanf("%d", a+i); sum += a[i];}
    if(sum & 1) return puts("no quotation"), 0;
    for(int i = 100;i > 1;-- i){
        memcpy(tmp, a, sizeof tmp);
        int l = 1, r = n; bool f = true;
        for(int j = i;j;-- j){
            if(tmp[l] < j){f = false; break;} tmp[l] -= j;
            if(tmp[r] < j){f = false; break;} tmp[r] -= j;
            if(!tmp[l]) ++ l; if(!tmp[r]) -- r;
        } if(f) return printf("%d\n", i), 0;
    } puts(sum == 2 ? "1" : "no quotation");
}

2013-2014 ACM-ICPC Northeastern European Regional Contest (NEERC 13)

H Hack Protection

简单题。

I Interactive Interception

容易想到直接二分，可为何是对的呢...

感性理解 😦

#include<bits/stdc++.h>
using namespace std;
const int N = 103;
int lp, rp, lv, rv, l[N], r[N]; char op[5];
bool chmin(int &a, int b){if(a > b) return a = b, 1; return 0;}
bool chmax(int &a, int b){if(a < b) return a = b, 1; return 0;}
int main(){
    scanf("%d%d", &rp, &rv);
    for(int i = 0;lp < rp;++ i){
        int mid = lp + rp >> 1;
        printf("check %d %d\n", lp, mid);
        fflush(stdout); scanf("%s", op);
        if(op[0] == 'Y') rp = mid; else lp = mid+1;
        for(int j = 0;j < i;++ j){
            chmin(rv, (rp - l[j]) / (i - j));
            chmax(lv, (lp - r[j]) / (i - j));
        } l[i] = lp; r[i] = rp; lp += lv; rp += rv;
    } printf("answer %d\n", lp);
}

2016-2017 ACM-ICPC, Central Europe Regional Contest (CERC 16)

B Bipartite Blanket

根据 Hall 定理，一个二分图中，对于一个左部点的集合 \(S\)，存在一个匹配覆盖 \(S\) 当且仅当 \(\forall S_0\subseteq S,|\Gamma(S_0)|\ge |S_0|\)。右部点同理。

推广一下就可以知道，一个二分图中，对于一个点集 \(S=S_L+S_R\)，其中 \(S_L,S_R\) 分别是左、右部点的集合，则存在一个匹配覆盖 \(S\) 当且仅当对 \(S_L,S_R\) 分别存在一个匹配覆盖。

证明：\(\Rightarrow\) 显然，\(\Leftarrow\) 考虑覆盖 \(S_L\) 的匹配，从左向右连红边，\(S_R\) 的匹配从右向左连蓝边，这样形成的图每个点的入度和出度 \(\le 1\) 且红蓝相间，所以形成了一些环、链和孤立点。环显然都是偶环，可以直接取一半，链的结尾点不是 \(S\) 中的点，所以直接从链首取即可。孤立点不是 \(S\) 中的点，不需要管，于是就成功构造了方案，得证。

然后用高位前缀和判断是否存在匹配，再用 two-pointer 计数，时间复杂度 \(O(n2^m+m2^n)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 1<<20;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, siz[N], deg[2][20], w[2][20], v, val[N], adj[N]; LL ans;
bool ok[N]; char str[22]; vector<int> sl, sr;
void work(){
    for(int i = 1;i < (1<<n);++ i){
        val[i] = val[i & (i-1)] + w[0][__builtin_ctz(i)];
        adj[i] = adj[i & (i-1)] | deg[0][__builtin_ctz(i)];
        ok[i] = siz[adj[i]] >= siz[i];
    } ok[0] = true;
    for(int i = 0;i < n;++ i)
        for(int j = 0;j < (1<<n);++ j)
            if(!(j >> i & 1)) ok[j | (1<<i)] &= ok[j];
    for(int i = 0;i < (1<<n);++ i) if(ok[i]) sl.push_back(val[i]);
}
int main(){
    read(n); read(m);
    for(int i = 1;i < N;++ i) siz[i] = siz[i>>1] + (i&1);
    for(int i = 0;i < n;++ i){
        scanf("%s", str);
        for(int j = 0;j < m;++ j)
            if(str[j] == '1'){deg[0][i] |= 1 << j; deg[1][j] |= 1 << i;}
    }
    for(int i = 0;i < n;++ i) read(w[0][i]);
    for(int i = 0;i < m;++ i) read(w[1][i]); read(v);
    work(); swap(deg[0], deg[1]); swap(w[0], w[1]); swap(n, m); swap(sl, sr); work();
    sort(sl.begin(), sl.end()); sort(sr.begin(), sr.end(), greater<int>());
    int u = 0; for(int t : sl){while(u < sr.size() && sr[u] + t >= v) ++ u; ans += u;}
    printf("%lld\n", ans);
}

L Lost Logic

又被教做人了

显然是能成立的限制都要加上，但是因为 \(m\le 500\) 所以要优化一下。

若两个变量在三个解的取值都相同，那么连 xa -> xb 和 !xa -> !xb，然后只用考虑每两个值之间的限制，所以总共边数很少。

此时可能的解只有 \(256\) 种，直接枚举并暴力判断即可。

#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define PB push_back
using namespace std;
typedef long long LL;
typedef pair<LL, LL> pii;
const int N = 53, M = N*N;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0; bool f = false;
    for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
    if(f) x = -x;
}
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
inline bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, m, val[N], u[M], v[M], vis[8]; bool w1[M], w2[M]; char obuf[M], *O = obuf;
void print(int x){if(x > 9) print(x / 10); *O++ = x % 10 + '0';}
void print(char *s){while(*O = *s++) ++ O;}
void add(int a, bool b, int c, bool d){
    u[++m] = a; v[m] = c; w1[m] = b; w2[m] = d;
    if(!b) *O++ = '!'; *O++ = 'x'; print(a); print(" -> ");
    if(!d) *O++ = '!'; *O++ = 'x'; print(c); *O++ = '\n';
}
int main(){
    read(n);
    for(int i = 0, ch;i < 3;++ i)
        for(int j = 1;j <= n;++ j){read(ch); val[j] |= ch << i;}
    for(int i = 1;i <= n;++ i)
        if(!vis[val[i]]) vis[val[i]] = i;
        else {add(vis[val[i]], 0, i, 0); add(vis[val[i]], 1, i, 1);}
    int cc = 0, tmp = 0; for(int i = 0;i < 8;++ i) cc += !vis[i];
    for(int i = 0;i < 8;++ i) if(vis[i])
        for(int j = 0;j < 8;++ j) if(vis[j])
            for(int a = 0;a < 2;++ a)
                for(int b = 0;b < 2;++ b) if(i != j || a != b){
                    bool f = true;
                    for(int c = 0;c < 3 && f;++ c)
                        if((i >> c & 1) == a && (j >> c & 1) != b)
                            f = false;
                    if(f) add(vis[i], a, vis[j], b);
                }
    for(int S = 0;S < 256;++ S){
        bool f = true;
        for(int i = 1;i <= m && f;++ i)
            if((S >> val[u[i]] & 1) == w1[i] && (S >> val[v[i]] & 1) != w2[i])
                f = false;
        if(f) ++ tmp;
    } if(tmp > (3 << cc)){puts("-1"); return 0;} printf("%d\n", m);
    fwrite(obuf, O - obuf, 1, stdout);
}

J Jazz Journey

所有点对可以分别处理，然后贪心即可。

2015-2016 ACM-ICPC, Central Europe Regional Contest (CERC 15)

F Frightful Formula

分类讨论 \(a=1\) 和 \(a\ne 1,b=1\) 和 \(b\ne 1\)，然后就可以将 \(c\) 消掉，就只用考虑第一行和第一列的贡献。

2013-2014 ACM ICPC Central European Regional Contest (CERC 13)

H Chain & Co.

相同方向的矩形之间不可能满足条件，于是只用考虑 \(3\) 种方向分成的 \(3\) 类之间是否满足条件。

2015-2016 ACM-ICPC, NEERC, Northern Subregional Contest

D Distribution in Metagonia

每次尽可能将 \(n\) 除以 \(2\) 然后再减去 \(3^{\lfloor\log_3 n\rfloor}\)，容易知道这样得到的解的 \(2\) 的次幂严格递增而 \(3\) 的次幂严格递减。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int t; LL n, pw[38]; vector<LL> ans;
int main(){
    freopen("distribution.in", "r", stdin);
    freopen("distribution.out", "w", stdout);
    read(t); pw[0] = 1;
    for(int i = 1;i < 38;++ i) pw[i] = pw[i-1] * 3;
    while(t --){
        read(n); int tt = 0; ans.clear();
        while(n){
            while(!(n & 1)){++ tt; n >>= 1;}
            LL p = *(upper_bound(pw, pw + 38, n) - 1);
            ans.push_back(p << tt); n -= p;
        } printf("%ld\n", ans.size());
        for(LL v : ans) printf("%lld ", v); putchar('\n');
    }
}

G Graph

神奇贪心...

用两个 priority_queue \(q1,q2\) 分别维护当前入度为 \(0\) 的点（小根堆）和当前需要入边的点（大根堆）。

每次尽可能将 \(q1\) 中的点弾到 \(q2\) 中（至少剩下一个，每次消耗一条边），然后若还有剩余，则看 \(q1\) 的最小值 \(u\) 与 \(q2\) 的最大值 \(v\) 哪个更大，若 \(u\) 更大，则之后再连向它显然是无用的，直接将其加入答案的拓扑序；若 \(v\) 更大，则为了防止 \(v\) 跑到前面去，必须将其加入答案的拓扑序并连边，然后将 \(u\) 从 \(q1\) 加到 \(q2\)。

若一开始 \(q1\) 就为空则直接将 \(q2\) 中的点按顺序加入拓扑序。（此时可以直接连边，因为消耗是已经“预支”过的）

#include<bits/stdc++.h>
#define MP make_pair
#define PB push_back
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0; bool f = false;
    for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
    if(f) x = -x;
}
int n, m, k, in[N], ans[N], head[N], to[N], nxt[N];
vector<pii> tmp;
priority_queue<int, vector<int>, greater<int> > q1;
priority_queue<int> q2;
void add(int a, int b){
    static int cnt = 0;
    to[++ cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;
}
int main(){
    freopen("graph.in", "r", stdin);
    freopen("graph.out", "w", stdout);
    read(n); read(m); read(k);
    for(int i = 0, u, v;i < m;++ i){read(u); read(v); add(u, v); ++ in[v];}
    for(int i = 1;i <= n;++ i) if(!in[i]) q1.push(i);
    for(int i = 1;i <= n;++ i){
        if(q1.empty()){tmp.PB(MP(ans[i-1], ans[i] = q2.top())); q2.pop();}
        else {
            while(k && q1.size() > 1){-- k; q2.push(q1.top()); q1.pop();}
            if(k && !q2.empty() && q1.top() < q2.top()){
                -- k; q2.push(q1.top()); q1.pop();
                tmp.PB(MP(ans[i-1], ans[i] = q2.top())); q2.pop();
            } else {ans[i] = q1.top(); q1.pop();}
        }
        for(int j = head[ans[i]];j;j = nxt[j]) if(!-- in[to[j]]) q1.push(to[j]);
    } for(int i = 1;i <= n;++ i) printf("%d%c", ans[i], " \n"[i == n]);
    printf("%ld\n", tmp.size()); for(pii o : tmp) printf("%d %d\n", o.fi, o.se);
}

I Insider's Information

调整法可过，但其实有保证正确的做法。

先做一次拓扑排序，使得 \(b\) 至少比 \(a,c\) 中的一个先出现（数据范围保证了一定可以做到）

从中间向两边扩展，假设当前点是一个限制里面最后一个出现的，那么限制就转化为了必须加到左边或必须加到右边，取较多的一边就可以满足至少一半的限制。

#include<bits/stdc++.h>
#define PB push_back
using namespace std;
const int N = 100003;
template<typename T>
void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, a[N], b[N], c[N], deg[N], q[N], f, r, id[N], ans[N], pl = 1, pr; bool vis[N];
vector<int> vec[N], tmp;
int main(){
    freopen("insider.in", "r", stdin);
    freopen("insider.out", "w", stdout);
    read(n); read(m);
    for(int i = 1;i <= m;++ i){
        read(a[i]); read(b[i]); read(c[i]);
        ++ deg[b[i]]; vec[a[i]].PB(i); vec[c[i]].PB(i);
    }
    for(int i = 1;i <= n;++ i) if(!deg[i]) q[r++] = i;
    while(f < r){
        int u = q[f++]; tmp.clear();
        for(int v : vec[u]) if(!vis[v]){
            vis[v] = true; tmp.PB(v);
            if(!--deg[b[v]]) q[r++] = b[v];
        } vec[u] = tmp;
    }
    for(int _ = n-1;~_;-- _){
        int tmp = 0;
        for(int i : vec[q[_]])
            if(id[a[i] ^ c[i] ^ q[_]] > id[b[i]]) ++ tmp;
            else -- tmp;
        id[q[_]] = tmp > 0 ? -- pl : ++ pr;
    }
    for(int i = 1;i <= n;++ i) ans[id[i] - pl + 1] = i;
    for(int i = 1;i <= n;++ i) printf("%d ", ans[i]);
}

2017-2018 ACM-ICPC, Central Europe Regional Contest (CERC 17)

C Cumulative Code

由于 \(md\le 2^k\)，所以当 \(m\le d\) 时直接暴力，\(m>d\) 时考虑 prufer 序列的一些性质，如对于大部分相同层的子树的 prufer 序列可以通过其中一个整体加得到，于是按除以 \(d\) 的余数先预处理，再进行查询。时间复杂度 \(O(qk2^{\frac k2})\)。

实现好烦，心态爆炸了...

D Donut Drone

询问可以对每个点维护 \(next\)，对第一列每个点维护走 \(c\) 步之后到达哪一个点，用 \(O(r)\) 步找循环节之后走 \(O(c)\) 步即可。

单点修改 \(next\) 对第一列的影响是一个区间赋值，用 \(O(c)\) 步可以求出来这个区间，\(O(r)\) 暴力区间赋值。

时间复杂度 \(O(m(r+c))\)。

posted @ 2020-11-04 18:18  mizu164  阅读(561)  评论(0)  编辑  收藏  举报