欧拉函数

欧拉函数

定义：表示小于n且与n互质的正整数的个数
用\(\varphi (n)\) 或者phi(n)表示
通式：\(\varphi(x)=x\prod\limits_{i=1}^{n}1-\frac{1}{p_i}=x\prod\limits_{i=1}^{n}\frac{p_i-1}{p_i}\)
\(p_i\)为x的所有质因数
\(\varphi(1)=1\)

积性：if gcd(a,b)=1, \(\varphi(a,b)=\varphi(a)\varphi(b)\)

证明：

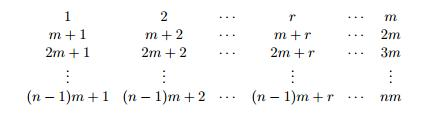
第k列可以表示为 \(km+r\)，因为\(gcd(km+r,m)=gcd(r,m)\) 所以与m互质的列有\(\varphi(m)\)个
互质的列每行构成\(mod\text{ }n\)的剩余系,剩余系中与n互质的个数为\(\varphi(n)\)
故与m,n互质的个数为行\(\times\)列,即\(\varphi(m)\times\varphi(n)\)

小性质：\(p|n,p^2|n,\varphi(n)=\varphi(n/p)\times p\)

证明：n,n/p有相同质因子令\(\prod\limits_{i=1}^{n}\frac{p_i-1}{p_i}=A\),\(\varphi(n)=n\times A\text{,}\varphi(n/p)=n/p\times A\)

CODE1(\(\sqrt{n}\)):

int euler(int x){
 int ans=x;
 for(int p=2;p<=sqrt(x);++p){
       if(x%p==0){
       ans=ans/p*(p-1);
       while(x%p==0)x/=p;
       }
 }
 if(x>1)ans=ans/x*(x-1);
 return ans;
}//根据通式

CODE2(n)

inline void euler(int n){
   for(int i=2;i<=n;++i){
    if(!v[i]){
     v[i]=i;
        p[++tot]=i;
        phi[i]=i-1;
      }
    for(int j=1;j<=tot;++j){
     if(p[j]>v[i]||p[j]*i>n)break;
     v[i*p[j]]=p[j];
     phi[i*p[j]]=phi[i]*(i%p[j]?p[j]-1:p[j]);//根据积性函数和小性质
      }
   }
}