HOROWITZ
Horowitz-Ostrogradsky方法
Hermite方法避免了完全分解,但仍要求无平方分解和关于![]() 的部分分式分解。Horowitz-Ostrogradsky方法则不需要其他工具,通过待定系数法将问题归结为线性方程的求解问题。
的部分分式分解。Horowitz-Ostrogradsky方法则不需要其他工具,通过待定系数法将问题归结为线性方程的求解问题。
设![]() 其中
其中![]() 为积分的有理部分,由部分分式的结果可知
为积分的有理部分,由部分分式的结果可知![]() ,
,![]() 。求导得到
。求导得到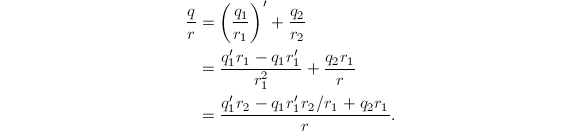 从而问题归结为求
从而问题归结为求![]() ,
,![]() 满足
满足![]() 且
且![]() ,
,![]() 。以
。以![]() ,
,![]() 的系数作为未知变量,这是一个至多
的系数作为未知变量,这是一个至多![]() 维的线性方程组问题。
维的线性方程组问题。
注1 设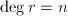 ,则Hermite方法的时间复杂度为
,则Hermite方法的时间复杂度为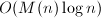 [3],其中
[3],其中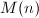 为乘法的复杂度。而Horowitz-Ostrogradsky方法的复杂度为
为乘法的复杂度。而Horowitz-Ostrogradsky方法的复杂度为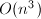 (解线性方程组),尽管渐进意义上后者要比前者慢将近两个量级,但在实践中还是要分析具体情况而定。
(解线性方程组),尽管渐进意义上后者要比前者慢将近两个量级,但在实践中还是要分析具体情况而定。
 Rothstein-Trager方法
Rothstein-Trager方法
下面的问题是如何求出对数部分,因此我们设![]() 无平方因子的首一多项式,并可设
无平方因子的首一多项式,并可设![]() 其中
其中![]() 为互不相同的常数,
为互不相同的常数,![]() 为无平方因子的首一多项式,两两互素(可以通过合并项来满足这些条件)。求导得到
为无平方因子的首一多项式,两两互素(可以通过合并项来满足这些条件)。求导得到![]() 由于
由于![]() 无平方因子且两两互素可知
无平方因子且两两互素可知![]() 记
记![]() ,则有
,则有![]() 及
及![]() 于是对于
于是对于![]()
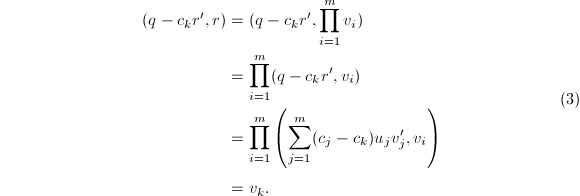 最后一个等式成立是因为
最后一个等式成立是因为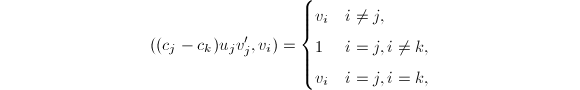 从而
从而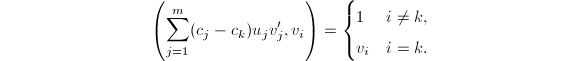
由式(3)可以看出,当我们找出系数![]() 后即可通过最大公因子的计算求出
后即可通过最大公因子的计算求出![]() 。如何求出
。如何求出![]() 呢?同样的论证可以知道
呢?同样的论证可以知道![]() ,而
,而![]() (此结式称为Rothstein-Trager结式),故求解关于
(此结式称为Rothstein-Trager结式),故求解关于![]() 的方程
的方程![]() 即可得到所有的系数
即可得到所有的系数![]() 。
。
例2 设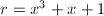 ,
,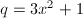 ,则Rothstein-Trager结式
,则Rothstein-Trager结式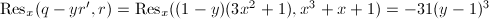 。从而方程
。从而方程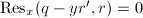 有唯一的根
有唯一的根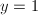 ,最大公因子
,最大公因子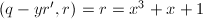 ,故
,故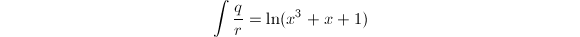 即为积分结果。 ◇
即为积分结果。 ◇
注2 Rothstein-Trager方法的时间复杂度为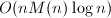 [3]。
[3]。
注3 对于高次Rothstein-Trager结式,其根可能无法显式地表达出来。设 无平方因子,
无平方因子,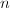 个根为
个根为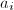 (
(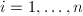 ),不难求得(1)中的
),不难求得(1)中的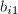 ,此时可直接将积分表示为
,此时可直接将积分表示为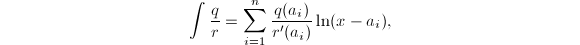 便于进一步的运算。
便于进一步的运算。

