Atcoder ABC 353 全题解
最近看的人好少……都快不想写了……
你们的支持就是我创作的最大动力!
AB
%你
CDE
题意:有一个一个一个函数,把函数两两配对式求值,求这些值最后的总和
C
考虑将所有的和减去 $ 10^8 $ 出现的次数。
将整个数组排序,然后进行二分,求第一个与这个数的和 $ \ge 10^8 $ 的位置,然后与这个数的位置取 max,看后面的数的数量即可。
// Problem: C - Sigma Problem
// Contest: AtCoder - AtCoder Beginner Contest 353
// URL: https://atcoder.jp/contests/abc353/tasks/abc353_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 100000000ll
ll a[300005];
int main() {
int n;
scanf("%d", &n);
ll ans = 0;
for (int i = 0; i < n; i++) {
scanf("%lld", &a[i]);
ans += a[i] * (n - 1);
}
sort(a, a + n);
for (int i = 0; i < n; i++) {
int cnt = n - max((int)(lower_bound(a, a + n, mod - a[i]) - a), i + 1);
ans -= mod * cnt;
}
printf("%lld", ans);
}
D
两个数拼凑,比如 $ a $ 位的 $ x $ 和 $ b $ 位的 $ y $,组成的数为 $ 10^bx + y $。
因此,我们可以考虑每个数的 $ 10^b $,那么一个数对答案的贡献,就等于它后面的数的 $ 10^b $ 之和,加上前面的数的数量,再将和乘上自己得到的结果。
可以倒序扫描,也可以用后缀和。
// Problem: D - Another Sigma Problem
// Contest: AtCoder - AtCoder Beginner Contest 353
// URL: https://atcoder.jp/contests/abc353/tasks/abc353_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 998244353
ll a[200005], suf[200005];
ll prod[200005];
ll calc_prod(ll x) {
ll ans = 1;
while (x) {
ans *= 10;
x /= 10;
}
return ans;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%lld", &a[i]);
suf[i] = a[i];
prod[i] = calc_prod(a[i]);
a[i] %= mod;
}
for (int i = n - 1; i >= 0; i--) {
suf[i] = (suf[i] + suf[i + 1]) % mod;
prod[i] = (prod[i] + prod[i + 1]) % mod;
}
ll ans = 0;
for (int i = 0; i < n; i++) {
ans = (ans + a[i] * prod[i + 1] % mod + suf[i + 1]) % mod;
}
printf("%lld", ans);
}
E
前缀?Trie 树走上!
先把所有字符串插进去,然后进行 dfs 或遍历。
对于一个节点,统计里面的字符串数量 $ n $,那么答案就会额外加 $ \frac{n(n - 1)}{2} $。
// Problem: E - Yet Another Sigma Problem
// Contest: AtCoder - AtCoder Beginner Contest 353
// URL: https://atcoder.jp/contests/abc353/tasks/abc353_e
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int trie[300005][26];
ll val[300005], cnt = 1;
void insert(string s) {
int node = 0;
val[0]++;
for (char x : s) {
if (trie[node][x - 'a'] == -1) {
trie[node][x - 'a'] = cnt++;
}
node = trie[node][x - 'a'];
val[node]++;
}
}
int main() {
memset(trie, -1, sizeof trie);
int n;
cin >> n;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
insert(s);
}
ll ans = 0;
for (int i = 1; i < cnt; i++) {
ans += val[i] * (val[i] - 1) / 2;
}
printf("%lld", ans);
}
F
首先在一个标准方格纸上走,找出最坏情况。
接着,考虑三种情况:
-
$ L \to L $
-
$ L \to S $
-
$ S \to S $
(第二种包括了 $ S \to L $)
首先考虑核心的第一种情况。
从一个大块走到斜对角相邻的另一个大块,可以从它们夹着的小块过去,代价为2,那么一般来说,代价就是坐标除以 $ K $ 后的切比雪夫距离乘 2。
但是也有特例:
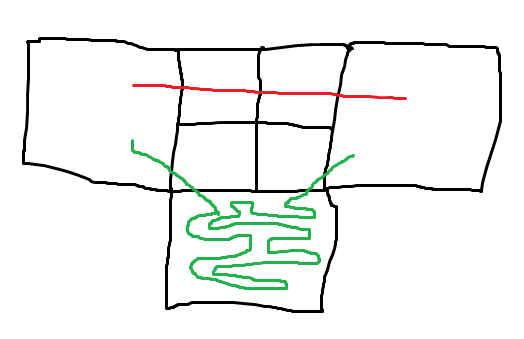
这时候就应该走红色而非绿色。
那怎么办?没办法,只能特判 $ K = 2 $ 的情况!
有了 $ L \to L $ 的基础,23 两类情况就很好处理了,先枚举一个方向从 $ S $ 走到 $ L $,然后再 $ L \to L $ 处理即可。
// Problem: F - Tile Distance
// Contest: AtCoder - AtCoder Beginner Contest 353
// URL: https://atcoder.jp/contests/abc353/tasks/abc353_f
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
bool large(ll bx, ll by) {
return (bx + by) & 1;
}
// X-1,X+1,Y-1,Y+1
ll s_to_l(ll x, ll y, ll sz, int dir) {
x %= sz, y %= sz;
if (dir == 0) {
return x + 1;
} else if (dir == 1) {
return sz - x;
} else if (dir == 2) {
return y + 1;
} else {
return sz - y;
}
}
ll dis_l(ll bx1, ll by1, ll bx2, ll by2, ll sz) {
if (sz == 1) {
return abs(bx1 - bx2) + abs(by1 - by2);
} else if (sz == 2) {
ll ans = min(abs(bx1 - bx2), abs(by1 - by2)) * 2;
ans += (max(abs(bx1 - bx2), abs(by1 - by2)) - min(abs(bx1 - bx2), abs(by1 - by2))) / 2 * 3;
return ans;
}
return max(abs(bx1 - bx2), abs(by1 - by2)) * 2;
}
ll dx[] = {-1, 1, 0, 0};
ll dy[] = {0, 0, -1, 1};
int main() {
ll sz;
scanf("%lld", &sz);
ll sx, sy, tx, ty;
scanf("%lld %lld", &sx, &sy);
scanf("%lld %lld", &tx, &ty);
ll bsx = sx / sz, bsy = sy / sz, btx = tx / sz, bty = ty / sz;
ll ans = abs(sx - tx) + abs(sy - ty);
if (sz == 1) {
printf("%lld", ans);
return 0;
}
if (large(bsx, bsy) && large(btx, bty)) {
printf("%lld", dis_l(bsx, bsy, btx, bty, sz));
} else if (!large(bsx, bsy) && !large(btx, bty)) {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
// cerr << i << " " << j << " ";
// cerr << s_to_l(sx, sy, sz, i) << " " << s_to_l(sx, sy, sz, j);
// cerr << " " << dis_l(bsx + dx[i], bsy + dy[i], btx + dx[j], bty + dy[j]) << endl;
ans = min(ans, s_to_l(sx, sy, sz, i) + s_to_l(tx, ty, sz, j) + dis_l(bsx + dx[i], bsy + dy[i], btx + dx[j], bty + dy[j], sz));
}
}
printf("%lld", ans);
} else {
if (!large(bsx, bsy)) {
swap(bsx, btx);
swap(bsy, bty);
swap(sx, tx);
swap(sy, ty);
}
for (int i = 0; i < 4; i++) {
ans = min(ans, s_to_l(tx, ty, sz, i) + dis_l(bsx, bsy, btx + dx[i], bty + dy[i], sz));
}
printf("%lld", ans);
}
}
G
考虑 DP,设 $ f_i $ 为我们必须参加第 $ i $ 场最多能赚到的钱。
聪明的你肯定已经想到了一个 $ O(n^2) $ 的 DP:
把转移分成两部分,从前面过来和从后面过来。
然后你就会发现,从前面过来的,由于 $ x_i > x_j $,所以可以把绝对值符号去掉!
那么,我们定一个“虚拟起点”,这个点位于所有点的后面。容易发现,从前面转移来的时候,从“虚拟起点”计算代价和从真正的点计算代价,大小关系以及差的关系仍然保持一致。
后面的同理。
现在,我们只有一个转移的起点了(即“虚拟起点”),那么我们就可以用树状数组进行单点更新,前缀查询 max 进行转移了,时间复杂度 $ O(n \ \log \ n) $。
// Problem: G - Merchant Takahashi
// Contest: AtCoder - AtCoder Beginner Contest 353
// URL: https://atcoder.jp/contests/abc353/tasks/abc353_g
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n;
ll cost, pre_bit[200005], suf_bit[200005], f[200005];
void update(int i, ll x) {
int p = i;
int j = n - i + 1;
while (i < 200003) {
pre_bit[i] = max(pre_bit[i], x - cost * (n - p)); // 虚拟起点 n
i += (i & -i);
}
while (j < 200003) {
suf_bit[j] = max(suf_bit[j], x - cost * p); // 虚拟起点 0
j += (j & -j);
}
}
ll query(int i) {
int p = i;
int j = n - i + 1;
ll ans = -0x3f3f3f3f3f3f3f3fll;
while (i) {
ans = max(ans, pre_bit[i] + cost * (n - p));
i -= (i & -i);
}
while (j) {
ans = max(ans, suf_bit[j] + cost * p);
j -= (j & -j);
}
return ans;
}
int main() {
scanf("%d %lld", &n, &cost);
int m;
scanf("%d", &m);
memset(pre_bit, -0x3f, sizeof pre_bit);
memset(suf_bit, -0x3f, sizeof suf_bit);
update(1, 0);
ll ans = 0;
for (int i = 1; i <= m; i++) {
int t;
ll p;
scanf("%d %lld", &t, &p);
f[i] = query(t) + p;
// cerr << f[i] << endl;
ans = max(ans, f[i]);
update(t, f[i]);
}
printf("%lld", ans);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号