OI loves Math（三）——组合数
又来了（喜）
这次我们聊组合数，也就是 $ C_n^m $ 。。。。。。
何为组合数
没人不知道吧。。。。。。
组合数就是问从 $ n $ 项里选 $ m $ 项有多少种选法，记作 $ C_n^m $ 或 $ \left( \begin{matrix} n \\ m \end{matrix} \right) $ 。
但是，竞赛中一般求 $ C_n^m \bmod 998244353 $ 。
怎么求
注：下文 $ mod $ 为模数。
有很多，但这儿介绍一种 $ O(n \log mod) $ 预处理，$ O(1) $ 单词查询的方法！
其实就是组合数公式。。。。。。
\[C_n^m = \frac{n!}{m!(n - m)!}
\]
再加上以前的逆元：
\[\frac{1}{x} \equiv x^{mod - 2} \pmod{mod}
\]
预处理 $ x! $ 和 $ x!^{mod - 2} \bmod mod $ 就可以了。
放一两段小代码：
prod[0] = 1, inv[0] = 1;
for (long long i = 1; i <= maxn; i++) {
prod[i] = prod[i - 1] * i % mod;
inv[i] = qpow(prod[i], mod - 2, mod);
}
long long C(long long n, long long m) {
return prod[n] * inv[n - m] % mod * inv[m] % mod;
}
例题
CF1717D
把选手按编号顺序排列：（注：转载于OIer某罗）
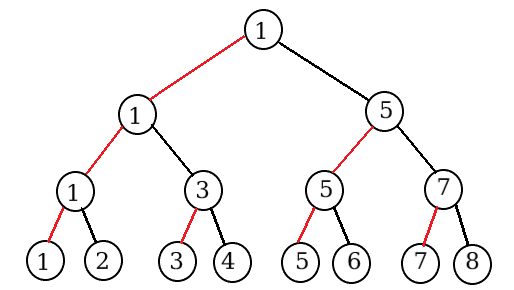
我们可以发现，选手 $ x $ 进行 $ x - 1 $ ，然后 $ \operatorname{popcount}(x - 1) $ 就是胜的场数。
那么问题就变成了求满足 $ \operatorname{popcount}(x) \le k \ \ \ (0 \le x \le 2^n - 1) $ 的 $ x $ 的个数，也就是 $ \sum _ {i = 0} ^ {\min \{ n, k \}} C _ {n} ^ {i} $
代码：
#include <bits/stdc++.h>
using namespace std;
long long prod[100005], inv[100005];
const long long mod = 1000000007;
long long qmul(long long base, long long exp, long long mod) {
long long ans = 0;
while (exp) {
if (exp & 1) {
ans = (ans + base) % mod;
}
exp >>= 1;
base = (base + base) % mod;
}
return ans;
}
long long qpow(long long base, long long exp, long long mod) {
long long ans = 1;
while (exp) {
if (exp & 1) {
// ans = qmul(ans, base, mod);
ans = ans * base % mod;
}
exp >>= 1;
// base = qmul(base, base, mod);
base = base * base % mod;
}
return ans;
}
long long C(long long n, long long m) {
return prod[n] * inv[n - m] % mod * inv[m] % mod;
}
int main() {
long long n, k;
scanf("%lld %lld", &n, &k);
long long ans = 0;
prod[0] = 1, inv[0] = 1;
k = min(n, k);
for (long long i = 1; i <= n; i++) {
prod[i] = prod[i - 1] * i % mod;
inv[i] = qpow(prod[i], mod - 2, mod);
}
for (long long i = 0; i <= k; i++) {
ans = (ans + C(n, i)) % mod;
}
printf("%lld", ans);
return 0;
}
再见！
