Hihocoder [Offer收割]编程练习赛8
A. 小Ho的强迫症 数论 GCD
题意:
一个人在无限长的路上走格子,步长为\(D\),脚长为\(F\),每个格子的长度为\(L\),如图所示:
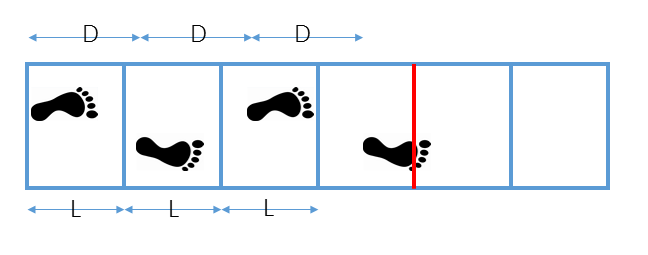
问能否一直走下去,永远踩不到线。
分析:
先不考虑脚的长度,观察一下在所有格子中落点的情况:
容易知道在每个格子中的落点到格子起点的距离都是\(g\),\(2g\),\(3g \cdots\),其中\(g=gcd(D, \; L)\)
即落点以\(g\)等间距地分布在格子上,所以如果脚长\(F>g\),一定会踩到格子的边线。
#include <cstdio>
int gcd(int a, int b) { return !b ? a : gcd(b, a%b); }
int main()
{
int T; scanf("%d", &T);
while(T--) {
int L, F, D; scanf("%d%d%d", &L, &F, &D);
int g = gcd(L, D);
if(F <= g) puts("YES");
else puts("NO");
}
return 0;
}
B. 拆字游戏 BFS
题意:
有一个\(01\)矩阵,求出所有四方向的连通块并输出。
分析:
找连通块可以用BFS,主要说一下这题的坑点:
- 代表点是连通块的最左且最上的点,而不是所在矩阵的左上角。
- 输出连通块所在矩阵时,注意不要输出其他连通块的\(1\)。
代码丑拒贴,(ˉ▽ ̄~)
C. 数组分拆 DP
题意:
给出一个长度为\(N(N \leq 10^5)\)的数组\(A_1 \sim A_N,|Ai| \leq 100\),求有多少种方案可以将数组划分若干段,且每段之和不为0,方案数对\(10^9 + 7\)取模。
分析:
设\(d_i\)为将前\(i\)个数划分为若干段且每段之和不为\(0\)的方案数
容易想到一个\(O(N^2)\)的做法:
预处理一下前缀和\(sum_i= \sum\limits_{j=1}^i A_j\)
对于前\(j\)个数的某个划分,如果\(sum_i-sum_j \neq 0\)的话,就可以将\(A_{j+1} \sim A_i\)作为后缀拼在后面得到一个前\(i\)个数的划分
所以转移方程为:\(d_i = \sum\limits_{j=0}^{i-1} d_j, sum_i - sum_{j-1} \neq 0\)
优化:\(d_i\)是由\(d_j\)拼接上不为\(0\)的后缀得到的,不如反向考虑,把所有可能的方案加起来然后减去那些后缀为\(0\)的不合法的方案。
设\(cnt_s\)表示元素之和为\(s\)的划分个数,如果某些划分和为\(sum_i\),说明它对应的后缀为\(0\)是不合法的,所以不合法的划分就有\(cnt_{sum_i}\)个。
因此\(d_i=\sum\limits_{j=1}^{i-1} d_j - cnt_{sum_i}\)
边界情况是\(d_0=1\),对应\(A_1 \sim A_i\)作为一个整体划分的转移
#include <cstdio>
#include <map>
using namespace std;
typedef long long LL;
const LL MOD = 1000000007LL;
void add(LL& a, LL b) { a += b; if(a >= MOD) a -= MOD; }
map<int, LL> M;
const int maxn = 100000 + 10;
int n, a[maxn], sum[maxn];
LL d[maxn];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%d", a + i);
sum[i] = sum[i - 1] + a[i];
}
M[0] = 1;
d[0] = 1;
LL tot = 1;
for(int i = 1; i <= n; i++) {
d[i] = (tot + MOD - M[sum[i]]) % MOD;
add(M[sum[i]], d[i]);
add(tot, d[i]);
}
printf("%lld\n", d[n]);
return 0;
}
D. 矩形计数 容斥原理
题意:
有一个\(N\)行\(M\)列的矩形,其中有\(K\)个黑格子,其余的都是白格子。
求全部由白格子组成的矩形的个数。
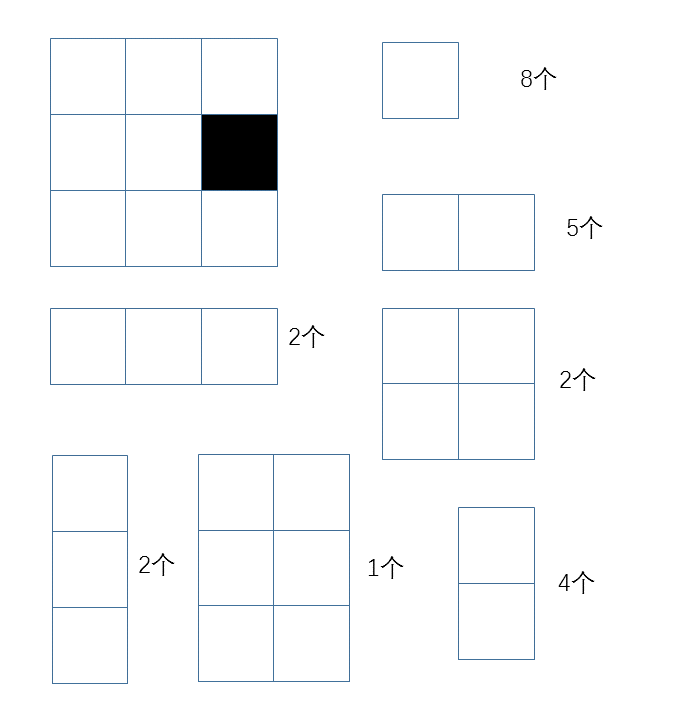
分析:
首先不考虑黑格子,计算出一共有多少个矩形:
枚举矩形的大小\(r \times c\),这样大小的矩形一共有\((N-r+1)(M-c+1)\)个。
然后减去不符合要求的矩形,也就是减去包含第一个黑格子的矩形个数,减去包含第二个黑格子,第三个的……
然后再加上包含第一第二黑格子的矩形数……
也就是容斥原理。
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
int n, m, k;
int r[10], c[10];
int main()
{
scanf("%d%d%d", &n, &m, &k);
LL ans = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
ans += (LL)(n + 1 - i) * (m + 1 - j);
for(int i = 0; i < k; i++)
scanf("%d%d", r + i, c + i);
for(int S = 1; S < (1 << k); S++) {
int lft = m + 1, top = n + 1;
int down = 0, rgh = 0;
int cnt = 0;
for(int i = 0; i < k; i++) if((S >> i) & 1) {
cnt++;
lft = min(lft, c[i]);
top = min(top, r[i]);
rgh = max(rgh, c[i]);
down = max(down, r[i]);
}
int sign = (cnt & 1) ? -1 : 1;
ans += (LL)sign * lft * (m + 1 - rgh) * top * (n + 1 - down);
}
printf("%lld\n", ans);
return 0;
}



