CodeForces 8D Two Friends 判断三个圆相交

题意：

有两个人\(Alan\)和\(Bob\)，他们现在都在\(A\)点，现在\(Bob\)想去\(B\)点，\(Alan\)想先到\(C\)点再去\(B\)点。
\(Alan\)所走的总路程不能超过\(T_1\)，\(Bob\)所走的总路程不能超过\(T_2\)。
求他们从\(A\)出发到第一次分开所能走的最长的公共路程。

分析：

首先特判一种特殊情况：
如果\(Bob\)能陪\(Alan\)走完全程，那么答案是\(min(T1, \, T2)\)。

因此他们一定是在\(Alan\)到达\(C\)之前分开的，否则如果在到达\(C\)之后再分开的话，显然不比一起回家更优。
然后二分答案x，即\(Alan\)和\(Bob\)走距离为x的相同路线后分开。
设分离点为\(P\)，那么点\(P\)必须满足一下三个条件：

• \(P\)必须在以\(A\)为圆心半径为\(x\)的圆内，因为他们走的公共距离为\(x\)
• \(P\)必须在以\(B\)为圆心半径为\(T_2-x\)的圆内，为了让\(Bob\)在分开之后能及时返回\(B\)点
• \(P\)必选在以\(C\)为圆心半径为\(T_1-x-BC\)的圆内，因为\(Alan\)在到达\(C\)之后还要径直走回\(B\)点。
  所以如果三个圆相交，那么一定存在这样的点\(P\)。

判断三个圆是否相交：
三个圆两两相交是必要条件但不是充分条件。
因为可能会有这种情况：

在两两相交的前提下，如果有一个小圆内含在一个大圆内的话，那么这三个圆也是相交的。
否则，如果三个圆有公共部分，两两圆必然有\(1 \sim 2\)个交点。
如图：

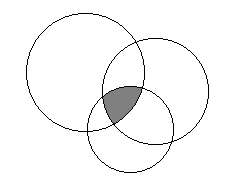
考虑这三个圆的相交区域，它必然是由若干个圆弧组成的。
所以这块区域的关键点也一定是某两个圆的交点，枚举两两圆的共三组交点，如果有一个交点满足都在三个圆的圆内或圆上，那么这三个圆就是相交的。

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;

typedef long double LD;
const LD eps = 1e-10;

int dcmp(LD x) {
	if(fabs(x) < eps) return 0;
	return x < 0 ? -1 : 1;
}

LD sqr(LD x) { return x * x; }

struct Point
{
	LD x, y;
	Point(LD x = 0, LD y = 0):x(x), y(y) {}
	void read() { cin >> x >> y; }
};

Point operator - (const Point& A, const Point& B) {
	return Point(A.x - B.x, A.y - B.y);
}

bool operator == (const Point& A, const Point& B) {
	return dcmp(A.x - B.x) == 0 && dcmp(A.y - B.x) == 0;
}

LD Dot(const Point& A, const Point& B) {
	return A.x * B.x + A.y * B.y;
}

LD Length(const Point& A) { return sqrt(Dot(A, A)); }

LD angle(const Point& A) { return atan2(A.y, A.x); }

struct Circle
{
	Point c;
	LD r;
	Circle() {}
	Circle(Point c, LD r):c(c), r(r) {}
	Point point(LD a) {
		return Point(c.x + cos(a) * r, c.y + sin(a) * r);
	}
};

LD t1, t2, T1, T2;
Point p[3];
Circle o[3];
vector<Point> inter;

bool OnCircle(Point p, Circle C) {
	return dcmp(Length(p - C.c) - C.r) == 0;
}

bool getCircleIntersection(Circle C1, Circle C2) {
	LD &r1 = C1.r, &r2 = C2.r;
	LD &x1 = C1.c.x, &x2 = C2.c.x, &y1 = C1.c.y, &y2 = C2.c.y;
	LD d = Length(C1.c - C2.c);
	if(dcmp(fabs(r1-r2) - d) > 0) return true;
	if(dcmp(r1 + r2 - d) < 0) return false;
	LD d2 = Dot(C1.c - C2.c, C1.c - C2.c);
	LD a = r1*(x1-x2)*2, b = r1*(y1-y2)*2, c = r2*r2-r1*r1-d*d;
	LD p = a*a+b*b, q = -a*c*2, r = c*c-b*b;

	LD cosa, sina, cosb, sinb;
	//One Intersection
	if(dcmp(d - (r1 + r2)) == 0 || dcmp(d - fabs(r1 - r2)) == 0) {
		cosa = -q / p / 2;
		sina = sqrt(1 - sqr(cosa));
		Point p(x1 + C1.r * cosa, y1 + C1.r * sina);
		if(!OnCircle(p, C2)) p.y = y1 - C1.r * sina;
		inter.push_back(p);
		return true;
	}
	//Two Intersections
	LD delta = sqrt(q * q - p * r * 4);
	cosa = (delta - q) / p / 2;
	cosb = (-delta - q) / p / 2;
	sina = sqrt(1 - sqr(cosa));
	sinb = sqrt(1 - sqr(cosb));
	Point p1(x1 + C1.r * cosa, y1 + C1.r * sina);
	Point p2(x1 + C1.r * cosb, y1 + C1.r * sinb);
	if(!OnCircle(p1, C2)) p1.y = y1 - C1.r * sina;
	if(!OnCircle(p2, C2)) p2.y = y1 - C1.r * sinb;
	if(p1 == p2)  p1.y = y1 - C1.r * sina;
	inter.push_back(p1);
	inter.push_back(p2);
	return true;
}

bool Include(Circle C1, Circle C2) {
	LD d = Length(C1.c - C2.c);
	if(dcmp(fabs(C1.r-C2.r) - d) > 0) return true;
	return false;
}

bool InAllCircle(const Point& t) {
	for(int i = 0; i < 3; i++) {
		LD d = Length(t - o[i].c);
		if(dcmp(d - o[i].r) > 0) return false;
	}
	return true;
}

bool check() {
	inter.clear();
	for(int i = 0; i < 3; i++)
		for(int j = i + 1; j < 3; j++)
			if(!getCircleIntersection(o[i], o[j])) return false;
	for(int i = 0; i < 3; i++)
		for(int j = i + 1; j < 3; j++)
			if(Include(o[i], o[j])) return true;
	for(Point t : inter)
		if(InAllCircle(t)) return true;
	return false;
}

int main()
{
	cout << fixed << setprecision(15);
	cin >> t1 >> t2;
	for(int i = 0; i < 3; i++) p[i].read();
	LD AB = Length(p[1] - p[0]);
	LD AC = Length(p[2] - p[0]);
	LD BC = Length(p[2] - p[1]);
	T1 = AC + BC + t1;
	T2 = AB + t2;
	
	if(dcmp(T2 - AC - BC) >= 0) {
		cout << min(T1, T2) << endl;
		return 0;
	}

	LD L = 0, R = min(T1 - BC, T2);
	for(int i = 0; i < 100; i++) {
		LD mid = (L + R) / 2.0;
		o[0] = Circle(p[0], mid);
		o[1] = Circle(p[1], T2 - mid);
		o[2] = Circle(p[2], T1 - BC - mid);
		if(check()) L = mid;
		else R = mid;
	}

	cout << L << endl;

	return 0;
}