最长公共子序列求方案数

题目链接

参考

在最长公共子序列问题中，状态的划分有两类：

1. \(a[i]==b[j]\)
   f[i][j]=f[i-1][j-1]+1;
2. \(a[i]!=b[j]\)
   f[i][j]=max(f[i-1][j],f[i][j-1],f[i-1][j-1])

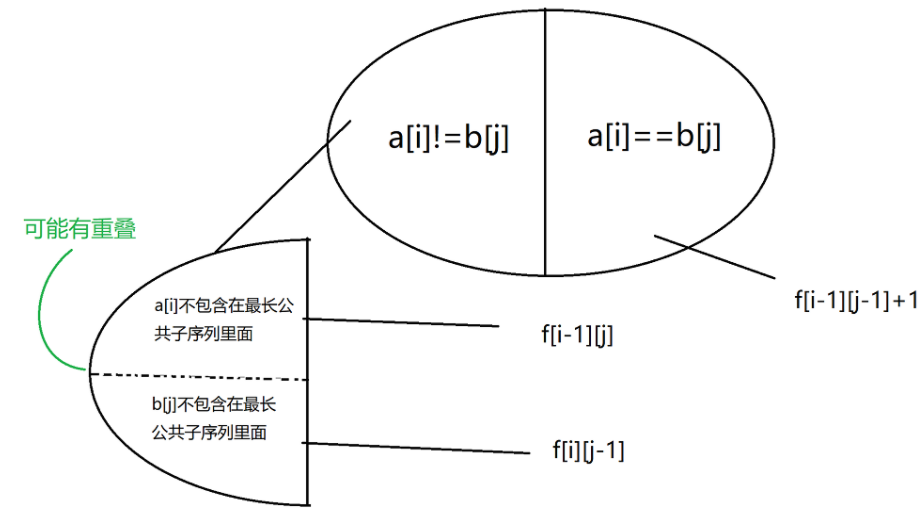
不过，考虑到 \(f[i-1][j-1]\) 可以通过 \(f[i-1][j]\) 或 \(f[i][j-1]\) 转移而来，我们通常将 \(a[i]!=b[j]\) 时的转移方程写为 \(f[i][j]=max(f[i-1][j],f[i][j-1])\)
可以发现，在这种划分方式中，我们仅仅做到了不漏，而没有做到不重，因为 \(f[i-1][j]\) 和 \(f[i][j-1]\) 都包含了 \(f[i-1][j-1]\)，因此在求方案数时，就有了一个大坑

和背包问题求方案数一样，我们令 \(cnt[n][m]\) 表示 \(a\) 的前 \(n\) 位和 \(b\) 的前 \(m\) 位构成最长公共子序列的方案数，然后在状态转移的时候维护好 \(cnt\) 即可

不过如上所说，有一个大坑，当 a[i]!=b[j]&&f[i][j]==f[i-1][j-1] 时，\(f[i][j]\) 会通过 \(f[i-1][j]\) 和 \(f[i][j-1]\) 转移，而 \(f[i-1][j]\) 和 \(f[i][j-1]\) 又都会通过 \(f[i-1][j-1]\) 进行转移，因此我们这里其实多转移了一次。
可以证明，当 a[i]!=b[j]&&f[i][j]==f[i-1][j-1] 时，必然有 \(f[i][j-1]==f[i-1][j]==f[i-1][j-1]\)，因为 \(a[i]!=b[j]\) 时，\(f[i][j]=max(f[i-1][j],f[i][j-1])=f[i-1][j-1]\)，不妨设 \(max(f[i-1][j],f[i][j-1])=f[i-1][j]\)，那么 \(f[i-1][j]==f[i-1][j-1]\)，且 \(f[i][j-1]<=f[i-1][j]=f[i-1][j-1]\)，又因为 \(f[i-1][j]\) 也可以通过 \(f[i-1][j-1]\) 转移，那么 \(f[i][j-1]>=f[i-1][j-1]\)，故 \(f[i][j-1]==f[i-1][j-1]==f[i-1][j]\)

故，代码如下：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 5010, mod = 1e8;

string a, b;
int n, m;
int f[N][N];
int cnt[N][N];

void print()
{
   for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            cout << cnt[i][j] << " \n"[j == m];
}

void init()
{
    cin >> a >> b;
    n = a.size() - 1, m = b.size() - 1;
    a = "#" + a, b = "#" + b;
    for(int i = 0; i <= m; i ++ )   cnt[0][i] = 1;
    for(int i = 0; i <= n; i ++ )   cnt[i][0] = 1;
}

void solve()
{
    // 计算 f
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            f[i][j] = max({f[i - 1][j], f[i][j - 1], f[i - 1][j - 1] + (a[i] == b[j])});
    // 计算 cnt
    for(int i = 1; i <= n; i ++ )
    {
        for(int j = 1; j <= m; j ++ )
        {
            int &u = cnt[i][j];
            // 不考虑重复的情况下三种可能的转移
            if(a[i] == b[j] && f[i][j] == f[i - 1][j - 1] + 1)  u = (u + cnt[i - 1][j - 1]) % mod;
            if(f[i][j] == f[i - 1][j])  u = (u + cnt[i - 1][j]) % mod;
            if(f[i][j] == f[i][j - 1])  u = (u + cnt[i][j - 1]) % mod;
            
            // 重复的情况
            if(a[i] != b[j] && f[i][j] == f[i - 1][j - 1])  u = ((u - cnt[i - 1][j - 1]) % mod + mod) % mod;
        }
    } 
    cout << f[n][m] << endl;
    cout << cnt[n][m] << endl; 
}

int main()
{
    init();
    solve();
    return 0;
}

注意，在 if(a[i] == b[j] && f[i][j] == f[i - 1][j - 1] + 1) u = (u + cnt[i - 1][j - 1]) % mod; 中，你不可以写为 if(f[i][j] == f[i - 1][j - 1] + 1) u = (u + cnt[i - 1][j - 1]) % mod;，因为此时 f[i][j] 不一定满足 a[i]==b[j]
同理 if(a[i] != b[j] && f[now][j] == f[pre][j - 1]) u = ((u - cnt[pre][j - 1]) % mod + mod) % mod;，不可以省去 if(a[i] != b[j]

滚动数组优化版本，优化掉一维

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 5010, mod = 1e8;

int n, m;
int f[2][N];
int cnt[2][N];
char a[N], b[N];

int main()
{
    scanf("%s%s", a + 1, b + 1);
    n = strlen(a + 1) - 1, m = strlen(b + 1) - 1;
    for(int i = 0; i < N; i ++ )   cnt[0 & i][i] = 1;
    for(int i = 0; i < N; i ++ )   cnt[i & 1][0] = 1;
    // 计算 cnt
    for(int i = 1; i <= n; i ++ )
    {
        int now = i & 1, pre = (i - 1) & 1;
        for(int j = 1; j <= m; j ++ )
        {
            // 计算f
            f[now][j] = max(f[pre][j], f[now][j - 1]);
            f[now][j] = max(f[now][j],f[pre][j - 1] + (a[i] == b[j]));
            // 滚动数组，利用上一层，清空当前层
            cnt[now][j] = 0;
            int &u = cnt[now][j];
            // 不考虑重复的情况下三种可能的转移
            if(a[i] == b[j] && f[now][j] == f[pre][j - 1] + 1)  u = (u + cnt[pre][j - 1]) % mod;
            if(f[now][j] == f[pre][j])  u = (u + cnt[pre][j]) % mod;
            if(f[now][j] == f[now][j - 1])  u = (u + cnt[now][j - 1]) % mod;
            
            // 重复的情况
            if(a[i] != b[j] && f[now][j] == f[pre][j - 1])  u = ((u - cnt[pre][j - 1]) % mod + mod) % mod;
        }
    } 
    printf("%d\n%d\n", f[n & 1][m], cnt[n & 1][m]);
    return 0;
}

另外，对于上面的证明，我们也可以验证：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cassert>

using namespace std;

const int N = 5010, mod = 1e8;

int n, m;
int f[2][N];
int cnt[2][N];
char a[N], b[N];

int main()
{
    scanf("%s%s", a + 1, b + 1);
    n = strlen(a + 1) - 1, m = strlen(b + 1) - 1;
    for(int i = 0; i < N; i ++ )   cnt[0 & i][i] = 1;
    for(int i = 0; i < N; i ++ )   cnt[i & 1][0] = 1;
    // 计算 cnt
    for(int i = 1; i <= n; i ++ )
    {
        int now = i & 1, pre = (i - 1) & 1;
        for(int j = 1; j <= m; j ++ )
        {
            // 计算f
            f[now][j] = max(f[pre][j], f[now][j - 1]);
            f[now][j] = max(f[now][j],f[pre][j - 1] + (a[i] == b[j]));
            // 滚动数组，利用上一层，清空当前层
            cnt[now][j] = 0;
            int &u = cnt[now][j];
            // 不考虑重复的情况下三种可能的转移
            if(a[i] == b[j] && f[now][j] == f[pre][j - 1] + 1)  u = (u + cnt[pre][j - 1]) % mod;
            if(f[now][j] == f[pre][j])  u = (u + cnt[pre][j]) % mod;
            if(f[now][j] == f[now][j - 1])  u = (u + cnt[now][j - 1]) % mod;
            
            // 重复的情况
            if(a[i] != b[j] && f[now][j] == f[pre][j - 1])  u = ((u - cnt[pre][j - 1]) % mod + mod) % mod;
            
            // 验证
            if(a[i] != b[j] && f[now][j] == f[pre][j-1])
                assert(f[now][j] == f[now][j - 1] && f[now][j] == f[pre][j]);
        }
    } 
    printf("%d\n%d\n", f[n & 1][m], cnt[n & 1][m]);
    return 0;
}