[蓝桥杯2020初赛] 平面分割及相关知识点补充
证明部分:
1.直线分割平面
一条直线要怎么样放置才能使得平面被分割为尽可能多的部分?

如果已经有了直线1,要让你添加一条直线,你会添加相交的还是平行的?
我们可以看到,如果添加直线2(平行),那么只会将直线1的上面部分一分为二;但是如果添加直线3(相交),那么将会将原有的两个部分都一分为二。
所以我们需要让添加的这条直线尽可能多的和原有的直线相交,并且添加的这条直线被分为了多少段,平面就会增加多少个部分。例如上图,在原有直线1的情况下, 加入直线3,那么直线3被切割为了两个部分,上面部分会上平面的上部分(直线1的上方)分割为两个部分,同理也会将平面的下部分(直线1的下方)分割为两个部分。
所以当我们加入第n条直线的时候,第n条直线最多被原有的n-1条直线切割为n段,平面也就最多增加n个部分,所以:
f(n) = f(n-1) + n
= f(n-2) + (n-1) + n
......
= f(1) + 2 + 3 ... + n
= 1 + 1 + 2 + 3 ... + n
= 1 + (n + 1) n / 2
2.原型分割平面

如图有两个圆形,如果我们已经有了圆形1,要添加一个圆形2,那么是相交还是不相交呢?
我们可以很容易的想到,如果相交的话,那么圆形2会被切割为两段,同直线的切割,平面也就会增加两个部分,而如果是不相交的话,圆形2就相当于只有一段,平面也就只会增加一个部分,所以我们也要让新添加的圆尽可能多的和原有的圆相交。
每和一个圆形相交就会有两个交点,所以加入第n个圆会产生2(n-1)个交点,也就是说这个圆会被切割为2(n-1)个部分,平面也就会增加2(n-1)个部分,所以:
g(n) = g(n-1) + 2(n-1)
= g(n-2) + 2(n-2) + 2(n-1)
......
= g(1) + 2 + 4 ... + 2(n-1)
= 2 + 2 + 4 ... + 2(n-1)
= 2 + (n-1) n
3.20个圆形和20条直线

如果有m个圆形0条直线,那么平面一共有2 + (m-1) m个部分
f(0) = g(m) = 2 + (m-1) m
这时候我们往其中依次加入直线:
- 每次加入一条直线,我们让直线和每一个圆都相交,那么会产生2m个交点,会将直线分为2m-1个线段和两条射线,一共将会新增加2m个部分,也就是说每一条直线加入只考虑原有的圆形的话都会新增加2m个部分,即:
f(1) = f(0) + 2m
= 2 + (m-1) m + 2m
2. 加入第二条直线,会和所有的圆增加2m个部分,和原有的直线会增加两个部分:
f(2) = f(1) + (2m + 2)
…
综上可进行推导:
f(n) = f(n-1) + (2m+n)
= f(n-2) + (2m+(n-1)) + (2m+n)
......
= f(1) + (2m+(2)) ... + (2m+n)
= (2 + (m-1) m) + (2mn) + 2 + 3 ... + n
= m^2 - m + 2mn + 1 + n(n+1) / 2
最后将m=20,n=20带入上式即可。
答案是1391
补充内容
总结一下一些平面分割的公式,以备查用
/**
* @file 平面分割(数学).cpp
* @brief 关于直线和圆分隔平面的问题总结
*/
#include <iostream>
#define ll long long
using namespace std;
/**
* @brief 计算n条直线最多能把平面分成几个部分
*
* @param n 直线条数
* @return ll 划分的块数
*/
ll cal_straight_line_divide(ll n) { return (n * n + n) / 2 + 1; }
/**
* @brief 计算n个圆最多能把平面分成几个部分
*
* @param n 圆的个数且n>=1
* @return ll 划分的块数
*/
ll cal_circle_divide(ll n) { return n * (n - 1) + 2; }
/**
* @brief 计算m个圆和n条直线最多能把平面分成几个部分
*
* @param m 圆的个数
* @param n 直线条数
* @return ll 划分的块数
*/
ll cal_circle_straight_line_divide(ll m, ll n) {
return m * m - m + 2 * m * n + n * (n + 1) / 2 + 1;
}
int main(void) {
ll n, m;
//依次输入直线条数和圆的个数
scanf("%lld%lld", &n, &m);
//直线
printf("%lld\n", cal_straight_line_divide(n));
//圆
printf("%lld\n", cal_circle_divide(n));
//直线和圆
printf("%lld\n", cal_circle_straight_line_divide(m, n));
return 0;
}
附加:三条边可以划分七个区域
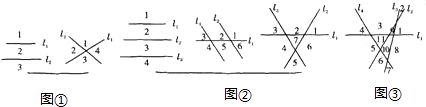
(1)如图①,两条直线可以把平面分成3或4个部分;如图②,三条直线可以把平面分成4或6或7个部分;
(2)如图③,四条直线最多可以把平面分成11部分;四条直线的位置关系:四条直线两两相交;
(3)一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,则n条最多可以把平面分成:an=1+(n+1)*n/2