递归函数和二分查找

递归函数

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身， 这个函数就是递归函数。

举个例子，我们来计算阶乘 n! = 1 x 2 x 3 x ... x n，用函数 fact(n) 表示，可以看出：

fact(n) = n! = 1 x 2 x 3 x ... x (n-1) x n = (n-1)! x n = fact(n-1) x n

所以,fact(n)可以表示为n*fact(n-1),只有 n = 1 时需要特殊处理.

于是,fact(n) 用递归的方式写出来就是:

def fact(n):

    if n == 1:
        return 1
    return n*fact(n-1)


上面就是一个递归函数.可以试试:

>>> fact(1)
1
>>> fact(5)
120
>>> fact(100)
9332621544394415268169923885626670049071596826438162146859296389521759999322991560894146397615651828625369792082722375825118521

递归函数的优点:

定义简单，逻辑清晰。理论上，所有的函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

递归次数的设置：

默认的递归次数:998

递归到一定的次数就会停止

import sys

sys.setrecursionlimit(10000)

 

 

 

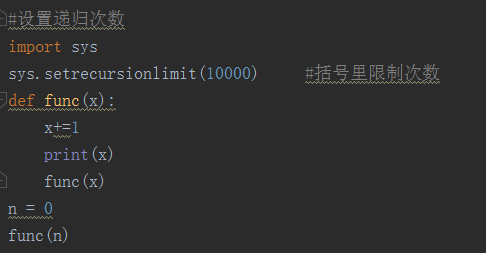
使用递归函数需要注意防止堆栈溢出。在计算机中，函数通用是通过栈（stack）这种数据结构实现的，没当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

 

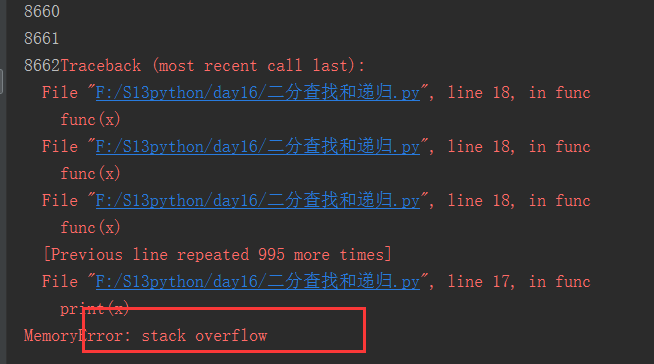
 可以看到这里的数据加载到8662的时候堆栈溢出，当然还有一个问题，那就是程序直接退出，俗称----掉了。和死循环有点相像。

 二分查找法

 假如有这样一个列表，让你找到其中的66，你会怎么做呢？

再假如，不用index来找数据呢，假如数据有几十万上百万呢，该怎么处理呢？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

 

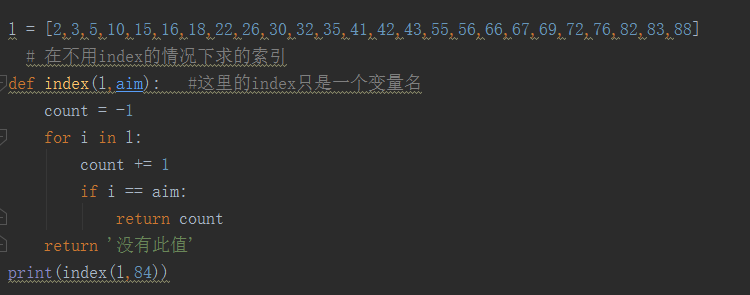
这就是一个简单的二分查找法。那么看出什么端倪了吗？

其实就是： 我有这么长的一个列表，加入我从中切一刀，一分为二，66在哪个区间我们就处理哪个区间。这样我想起了初中的一道数学题，一张纸0.01毫米，对折多少次能和珠穆朗玛峰一样高

结果就是 0.01*2**20 = 10485.76

这个和二分法有异曲同工之妙，唯一与之不同的便是二分法是切，折纸是合，不管多么庞大的数据我们都可以用二分法来处理，最终把它变成一个简单的数据。

l1 = [2, 3, 5, 10, 15, 16, 18, 19] def two_find(l1,aim,start = 0,end = None): end = len(l1)-1 if end is None else end #三元表达式 mid_index = (end - start) // 2 + start ''' 第一次: aim:15 start: 0 end: 6 min_index: 3 中间值:10 aim > 10 第二次: aim:15 start: 4 end: 6 min_index: 5 中间值:16 aim < 16 第三次: aim:15 start: 4 end: 5 min_index: 4 中间值:15 aim = 15 ''' if start <= end: if aim > l1[mid_index]: return two_find(l1,aim,start = mid_index + 1,end = end) elif aim < l1[mid_index]: return two_find(l1,aim,start = start,end = mid_index) elif aim == l1[mid_index]: return mid_index else: return None else: return None print(two_find(l1,15))