浅谈树状数组与线段树
树状数组和线段树都是用于维护数列信息的数据结构,支持单点/区间修改,单点/区间询问信息。以增加权值与询问区间权值和为例,其余的信息需要维护也都类似。时间复杂度均为\(O(logn)\)。
树状数组
对于树状数组,编号为\(x\)的结点上统计着[\(x-lowbit(x)+1,x\)]这一段区间的信息,\(x\)的父亲就是\(x+lowbit(x)\)。
如果不知道\(lowbit\)是啥的话可以去看看这个:https://www.cnblogs.com/AKMer/p/9698694.html
画出来就长这样:
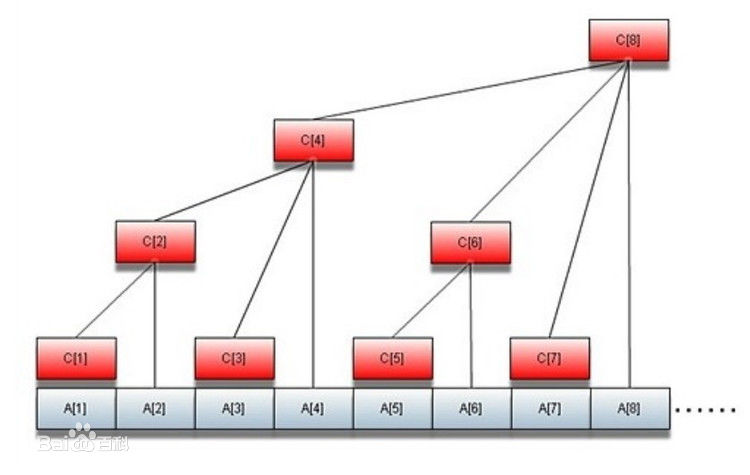
假设我们要维护的区间是\(A\)数组,那么\(C\)数组就是树状数组里存的东西。每个结点掌管的区间都是[\(x-lowbit(x)+1,x\)]。
单点修改区间查询
假设我们要令\(A_x\)增加\(v\),那么\(x\)以及\(x\)的所有祖先全部都需要增加\(v\),因为这些结点的统计区间全部都覆盖了\(x\)这个位置,而其他结点没有。
假设我们要询问区间[\(l,r\)]的权值和,我们可以转化为前缀和相减,也就是\(sum[r]-sum[l-1]\)。
假设我们要求\(sum[x]\),那么我们只需要每次加上当前结点\(x\)的权值,然后令\(x\)等于\(x-lowbit(x)\),直到\(x\)为1时停下来。因为\(x\)统计的是区间[\(x-lowbit(x)+1,x\)]的信息,所以前缀和就由若干个这样的区间组成,每次令\(x-=lowbit(x)\)就相当于去访问前面一个区间了。由于\(lowbit\)与\(x\)的二进制最低位的\(1\)有关,所以复杂度是\(O(logn)\)的。
代码如下:
#define low(i) ((i)&(-i))
void add(int pos,int v) {
for(int i=pos;i<=n;i+=low(i))
c[i]+=v;//单点修改
}
int query(int pos) {
int res=0;
for(int i=pos;i;i-=low(i))
res+=c[i];
return res;//询问区间[1,pos]的权值和
}
区间修改单点询问
这个要利用差分的思想就行了。每次在数组的\(l\)处加\(v\),\(r+1\)处减\(v\),然后一个数的权值就是\([1,x]\)的差分和。
代码如下:
#define low(i) ((i)&(-i))
int l=read(),r=read(),v=read();
add(l,v);add(r+1,-v);
int pos=read();
printf("%d\n",query(pos));//add与query函数见单点修改区间询问
区间修改区间询问
假设\(a\)是差分数组,那么前缀权值和就是\(a\)的前缀和的前缀和,也就是:
化开就是:
\(\sum\limits_{i=1}^{x}(x-i+1)a[i]=(x+1)\sum\limits_{i=1}^{x}a[i]-\sum\limits_{i=1}^{x}i*a[i]\)
同单点修改,我们只需要开两个树状数组,一个维护\(a[i]\),一个维护\(i*a[i]\)就行了。
代码如下:
#include <cstdio>
using namespace std;
typedef long long ll;
#define low(i) ((i)&(-i))
const int maxn=1e5+5;
int n,m;
ll a[maxn],sum[maxn];
ll read() {
ll x=0,f=1;char ch=getchar();
for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
return x*f;
}
struct TreeArray {
ll c[maxn];
void add(int pos,ll v) {
for(int i=pos;i<=n;i+=low(i))
c[i]+=v;
}
ll query(int pos) {
ll res=0;
for(int i=pos;i;i-=low(i))
res+=c[i];
return res;
}
}T1,T2;//T1维护a[i]的前缀和,T2维护i*a[i]的前缀和
int main() {
n=read(),m=read();
for(int i=1;i<=n;i++)
a[i]=read(),sum[i]=sum[i-1]+a[i];
for(int i=1;i<=m;i++) {
int opt=read(),l=read(),r=read();
if(opt==1) {//区间加
ll k=read();
T1.add(l,k);T1.add(r+1,-k);
T2.add(l,l*k);T2.add(r+1,-(r+1)*k);
}
else {//区间查询
ll ans=sum[r]-sum[l-1];
ans+=(r+1)*T1.query(r)-T2.query(r);
ans-=l*T1.query(l-1)-T2.query(l-1);
printf("%lld\n",ans);
}
}
return 0;
}
线段树
线段树是基于分治思想的数据结构,功能比树状数组更强大,长这样:
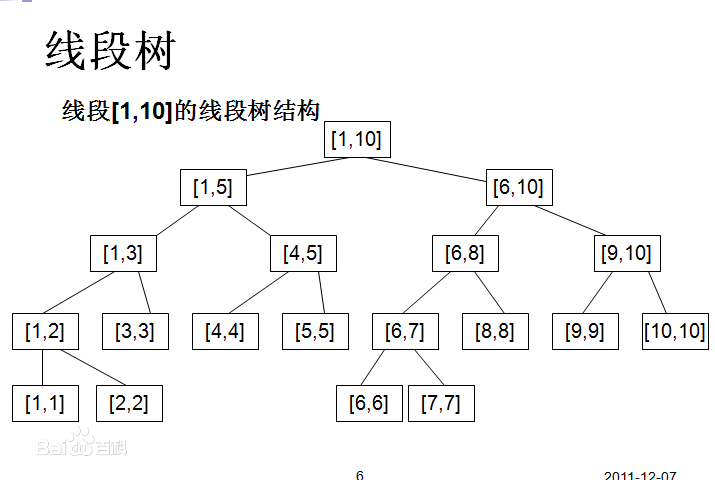
对于一个节点\(p\),如果他统计的区间是[\(l,r\)],\(mid=(l+r)/2\),那么他左儿子统计的区间就是\([l,mid]\),右儿子是\([mid+1,r]\)。对于某些节点统计的区间是\([x,x]\),那么就直接是单点的信息,每个点的信息可以由子节点合并更新。因为线段树是一颗二叉树,所以我们可以用\(p*2\)来记录\(p\)的左儿子,\(p*2+1\)记录右儿子。这样子的话,因为最后一层可能前面全部空出来,单出一个区间[\(n,n\)]在这一层的最后面,所以空间要开到\(4*n\)才不会段错误。
单点修改
直接从根开始,以覆盖\(x\)这个位置的区间为路径,将一条链上的节点全部更新。复杂度是\(O(logn)\)的。
代码如下:
void updata(int p) {
tree[p]=tree[p<<1]+tree[p<<1|1];
}
void change(int p,int l,int r,int pos,int v) {//更新p号节点,p号节点统计了[l,r]的信息,我要把pos位置的值增加v
if(l==r) {
tree[p]+=v;
return;
}//此时到一条链的最底部了就return
int mid=(l+r)>>1;
if(pos<=mid)change(p<<1,l,mid,pos,v);
else change(p<<1|1,mid+1,r,pos,v);//选择覆盖pos的路径递归
updata(p);//更新p节点的信息
}
//更改的时候调用change(1,1,n,x,v)就行了。
区间查询
假如当前区间被我需要访问的区间全部覆盖了,那么直接返回当前区间的权值和就行了。如果不是,再分情况讨论,分别去递归询问左儿子右儿子,再合并起来。显然,我会访问的节点全部是包含\(l\)与\(r\)的,不包含的话会在一开始就返回统计的权值,不会进行递归,所以复杂度也是\(O(logn)\)的。
代码如下:
int query(int p,int l,int r,int L,int R) {
if(L<=l&&r<=R)return tree[p];//如果当前区间是询问区间子区间就直接返回统计信息
int mid=(l+r)>>1,res=0;
if(L<=mid)res+=query(p<<1,l,mid,L,R);//如果L<=mid就返回[L,mid]的和
if(R>mid)res+=query(p<<1|1,mid+1,r,L,R);//如果R>mid就返回[mid+1,R]的和
return res;
}
延迟标记与区间修改
对于区间修改,如果我们一个一个值的去改的话,还不如\(n^2\)暴力统计信息的算法。所以就有了延迟标记这种东西。如果一个节点上面有延迟标记,就表示这个节点已经被修改过了,但是这个节点的子节点还没有被修改过,如果要进行递归必须要把延迟标记的影响一起带下去,然后把当前结点的延迟标记清空。对于一个区间[\(l,r\)],如果是我要修改的区间的子区间,那么我就直接把当前节点\(p\)的统计信息更新掉,然后打上延迟标记,就不进行递归一个一个改了。根据区间查询的复杂度,区间修改也只会在包含\(l\)与\(r\)的路径上进行递归,复杂度是\(O(logn)\)的。
代码如下:
void updata(int p) {
tree[p]=tree[p<<1]+tree[p<<1|1];
}
void add_tag(int p,int l,int r,int v) {
tree[p]+=(r-l+1)*v;tag[p]+=v;//标记只对儿子有影响,自己在打标记的同时一起把统计信息更改了。
}
void push_down(int p,int l,int r) {
int mid=(l+r)>>1;
add_tag(p<<1,l,mid,tag[p]);
add_tag(p<<1|1,mid+1,r,tag[p]);
tag[p]=0;//把当前标记分别传给两个儿子然后清空
}
void change(int p,int l,int r,int L,int R,int v) {//[l,r]为当前区间,[L,R]为要修改的区间
if(L<=l&&r<=R) {
add_tag(p,l,r,v);//打标记
return;
}
int mid=(l+r)>>1;push_down(p,l,r);//下传标记
if(L<=mid)change(p<<1,l,mid,L,R,v);
if(R>mid)change(p<<1|1,mid+1,r,L,R,v);//递归更改
updata(p);//更新当前结点的信息
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号