浅谈爬山算法

百度百科：https://baike.baidu.com/item/%E7%88%AC%E5%B1%B1%E7%AE%97%E6%B3%95/3252408?fr=aladdin

一句话总结爬山算法：一个在迷雾中试图攀爬珠峰的勇者爬上山峰的过程。

局部搜索算法

对于一些问题，状态空间十分的大，我们无法遍历全部状态空间，所以只能使用局部搜索算法。所谓局部搜索算法，就是只对局部的状态空间进行搜索，从而得出局部最优解的算法。这种算法的优点突显在不用考虑时空间，我们始终是在自己规定的状态空间内进行遍历，得出新的状态后替换掉旧的状态，保证局部状态空间大小不变。

而爬山算法，则是十分经典的一种局部搜索算法。

何为爬山？为什么爬山算法不叫下山算法而叫爬山算法呢？因为爬山算法将状态空间里每一个状态映射成一个个点，而状态的优秀度就是一个个点对应的函数值。对于一个函数，我们找到它的峰值，我们就找到了原问题的最优解。爬山算法做的，就是找多峰函数最优值的问题。

怎么爬

爬山很简单，从起始状态开始，哪里高往哪里爬。对于每个状态，都会有与之相邻的状态。在与它相邻的状态中，优秀度最高的那个邻居就是可能成为我们下一步的点。如果该点优秀度高于当前的点，那么就爬到那一个点去，否则说明我们已经爬到了山顶，那么当前所在的状态就是最优解。

不可忽视的致命短处——迷雾

之前就说过了，爬山是在迷雾中攀爬。也就是说，尽管你爬到了某个小山的山顶，但是因为大雾漫天，挡住了你的视线，所以你并不知道远处的珠峰更高。这是爬山算法的致命性短处，因为这一点，正确性无法得到十足的保证。爬山算法在大几率上会陷入局部最优解。
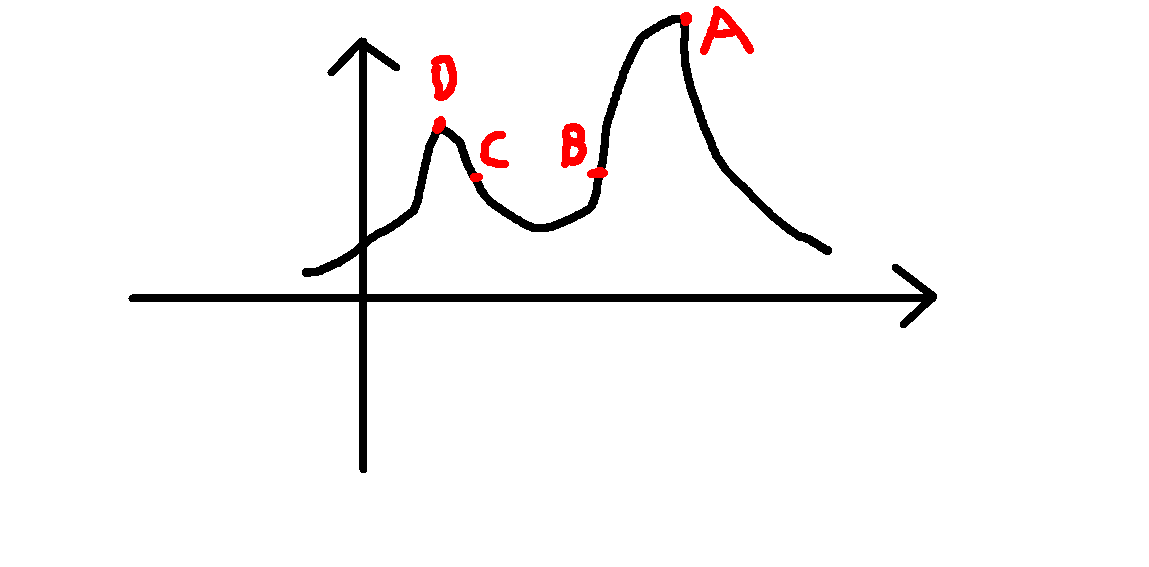
就如下图，如果你是从\(C\)点出发，那么就将以为\(D\)点是最优解而错过了真正的最优解\(A\)。相反，如果你从\(B\)点出发就可以获得正确答案。

人多力量大

于是乎，为了保证可以遍历到最优解，我们可以适当增加初始状态空间的大小（增加爬山的人数），然后从每一个起点出发，答案取最终山顶高度的最大值，便可以大大减小爬山出错的几率。

求函数\(f(x)\)峰值代码：

#include <ctime>
#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long

const int n=1000;//起点个数

int p[n+5];//存起始点

ll f(int x) {
	//返回函数值
}

ll climb(int x) {//爬山
	int pos=x;
	while(1) {
		int y=x+1,z=x-1,nxt;
		if(f(y)>f(z))nxt=y;
		else nxt=z;//找下一个点
		if(f(nxt)<f(pos))break;//如果当前点已经是峰顶就结束该过程
		pos=nxt;//否则就往更高的点爬
	}
	return f(pos);//返回峰顶函数值
}

int main() {
	srand(time(0));int f=1;
    for(int i=1;i<=n;i++)
		p[i]=rand()*f,f*=-1;//初始化状态空间
	ll ans=0;
	for(int i=1;i<=n;i++)
		ans=max(ans,climb(p[i]));//更新答案
	printf("%lld\n",ans);
    return 0;
}