浅谈遗传算法

先上百度百科：https://baike.baidu.com/item/%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3%95/838140

我学遗传的时候先看的百度百科……看的我一脸懵逼……然后有资料看了之后发现百度百科里只有第一段是给\(OIer\)看的，剩下的就是给生物竞赛的同学们看的了。

此后，我四处辗转，终于弄到了\(2002\)年国家集训队论文《遗传算法的特点及其应用》。感谢张宁大佬，让我学会了遗传算法。

遗传算法（Genetic Algorithms）的基本概念

遗传算法大多用于解决一类求最优解问题。基于达尔文的生物进化论，物竞天择，适者生存，是人工智能算法的的重要新分支。一些专有名词请点击百度百科了解一下。

遗传算法运行过程

遗传算法基于自然选择，在计算上模拟生物进化的过程。
在自然界的演化过程中，生物一代又一代的繁衍。他们遗传了上一代的优势，也可能会发生变异，但是留下来的，必然会越来越适应这个世界的环境。
遗传算法将状态当成染色体，状态里的每一个决策都是染色体上的一个基因。然后根据实际情况生成一个估价函数，计算每一串染色体对环境的适应度。让适应度高的遗传到下一代，适应度低的淘汰掉，过程中也许会发生变异，导致一些决策改变。所以估价函数是遗传算法就重要的一部分，你的遗传究竟是欧洲人发明的还是非洲人发明的就取决于估价函数的设定。像我这种非酋，就只能像下面两张图那样了……

为了便于估价函数的设计，我们一般用串来表示状态，常见的有\(2\)进制串与\(10\)进制串。
算法开始先随机生成一些染色体，作为一开始的祖先种群，然后不断繁衍。如果估价函数的最大值超过预先定义的\(T\)代一直都不变说明局面稳定下来了，就可以出结果了。或者直接判断当前代有最优解，那么就可以直接输出了。

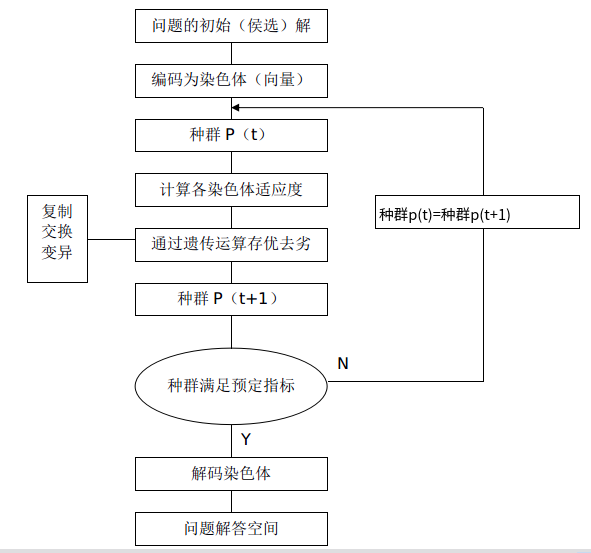
由于遗传算法是随机性近似算法，所以我们必须采取措施使其不收敛到局部最优解而是全局最优解，并且尽量提高达到最优解的概率。因此，遗传算法除了设计估价函数以外，还有很重要的三个部分：选择，交叉，变异。接下来我们详细的讲解一下。

一、选择

物竞天择，适者生存。假设我们有\(n\)条染色体，\(f[i]\)表示第\(i\)条染色体对周围环境的适应度。\(f\)就是估价函数。对于选择，有三种方法，各有利弊：

1、轮盘选择法

大家想象一下我们平常在商场看见过的轮盘抽奖活动。对于每一块不同的奖励占圆盘面积也不同，我们可以根据\(f[i]与\sum_{i=1}^nf[i]\)的比值来设定每一条染色体的比重，然后\(rand\)出n个染色体（可以重复rand出同一条）来形成下一代种群。
利：很好写并且很好理解。
弊：可能会忽视最优解，这的确是靠人品来选择，只不过适应度高的染色体会有大几率\(rand\)出来。然而爆率大也不表示100%可以抽中嘛。
代码实现：

void Roulette() {
    for(int i=1;i<=n;i++)
        sum[i]=sum[i-1]+f[i];//sum是f的前缀和
    for(int i=1;i<=n;i++) {
        int Pointer=random(sum[n])+1;//rand一个sum[n]以内的数
        for(int j=1;j<=n;j++)
            if(sum[j-1]<pointer&&pointer<=sum[j]) {//如果该数在j号染色体的比重内就把j号选择到下一代去
                new_chr[i]=chr[j];break;
            }
    }
    for(int i=1;i<=n;i++)
        chr[i]=new_chr[i];
}

2、确定选择法

跟轮盘选择法不同的是，确定选择法直接强行印点占比\(\frac{m}{n}\)的染色体会被选择到m次。这样不会出现全部抽中最坏的染色体的情况。
代码实现：

void certain() {
    int cnt=0;
    for(int i=1;i<=n;i++)
        sum[i]=sum[i-1]+f[i];//求f前缀和
    for(int i=1;i<=n;i++)
        g[i]=(int)(1.0*f[i]/sum[n]*n);//求分子m
    for(int i=1;i<=n;i++)
        for(int j=1;j<=g[i];j++)
            new_chr[++cnt]=chr[i];//选择m次，因为g数组是向下取整的所以最后cnt肯定不会超过n
    while(cnt<n)new_chr[++cnt]=chr[random(n)+1];
    for(int i=1;i<=n;i++)
        chr[i]=new_chr[i];
}

3、择优选择法

把适应度最大的染色体直接\(copy\)到下一代之后再做\(n-1\)遍轮盘选择法。可以保证最优解不会被扔掉而且也可以使得遗传过程更加充满“物竞天择”的意味。

交叉与变异的重要性

于是乎，选择就到此为止了。然而我们光选择的话是无法生存新的染色体的，所以我们还需要交叉和变异来使得我们可以获得初始种群里没有的染色体。这样可以避免开局不利导致全局不利。

二、交叉

我们随机选择两个染色体，然后随机一个点，然后把该点左边的部分全部交换。当然，你要是喜欢右边也没关系。但是因为这样可能会改变过大，所以我们也可以选择\(rand\)一个区间\([l,r]\)，把区间内的那一部分全部交换掉。
\(01010|1001|0101\)
\(10101|0101|0101\)
交换中间那一段之后就变成了
\(01010|0101|0101\)
\(10101|1001|0101\)
当然，如果交换使得两条染色体的适应度就降低了的话那么这次交换就是不明智的，所以我们应该放弃此次交换机会。
代码实现：

void cross() {
	for(int i=1;i<=10;i++) {//交叉10次，也可以其它次数
		int u=random(n)+1,v=random(n)+1;//u,v是我随机出来用于此次交叉的两条染色体
		int l=random(len)+1,r=random(len)+1;//l，r是我随机出来的区间
		if(l>r)swap(l,r);
		if(check(f[u],f[v],chr[u],chr[v],l,r))continue;//如果交叉之后会变得不优就放弃
		for(int i=l;i<=r;i++)
			swap(chr[u].gene[i],chr[v].gene[i]);
		f[u]=calc(chr[u]),f[v]=calc(chr[v]);//交叉之后重新计算适应度
	}
}

三、变异

随机一个染色体然后随机一个位置，然后改变那个基因。
\(101001100101\)的第\(3\)位发生了变异
就变成了\(100001100101\)
变异的概率是非常低的，尽量设在\(0.1\)以下
然后每一位的变异概率乘上基因总数就是变异次数。
代码实现：

void variety() {
	for(int i=1;i<=var_cnt;i++) {
		int u=random(n)+1,pos=random(len)+1;//随机一条染色体和要变异的位置
		life tmp=chr[u];tmp.gene[pos]^=1;
		if(calc(tmp)<f[u])continue;//如果变异不优我就不变
		chr[u].gene[pos]^=1;
		f[u]=calc(chr[u]);//否则变异，并且重新计算适应度
	}
}

就这样，遗传算的的全过程我们就弄完了。知道\(f_{max}\)超过\(T\)代都不改变，那么我们就可以从当前代里找最优解了。
理论讲完了，我们来个样例模拟一下这个过程吧。

IOI金牌的养成方法

作为一名\(IOI\)金牌的获得者，你肯定拥有超高的码力，超凡的毅力，超强的思维能力以及超长的\(OI\)学习生涯。我们用一个四位\(01\)串来表示以上条件是否满足。\(f[x]\)就是\(x\)号染色体的\(01\)串所表示十进制数值。自然，这个值越高就越接近\(IOI\)金牌的能力。
我们\(rand\)四个串来表示开始的四个\(OIer\)，看看遗传算法会在他们身上发生什么奇妙的效果，看看他们在交♂流与切♂磋过几代之后实力会不会有所提升。

编号	超强的思维能力	超高的码力	超凡的毅力	超长的\(OI\)学习生涯	\(01\)串
1	并没有	有！	有！	并没有	0110
2	并没有	并没有	有！	有！	0011
3	有！	有！	并没有	并没有	1100
4	并没有	有！	并没有	有！	0101

序号	染色体	适应度
1	0110	6
2	0011	3
3	1100	12
4	0101	5
适应度总和	-	26
最坏适应度	-	3
最好适应度	-	12
平均适应度	-	6.5

选择进入下一代的染色体

由表可知，所有染色体串适应度的总和是\(26\)，\(3\)号串的适应度是\(12\)，占适应度总和的\(\frac{6}{13}\)，也就是\(3\)号被选中的机会接近两次；\(1\)号，\(2\)号，\(4\)号被选中的概率分别是\(\frac{3}{13}\)，\(\frac{3}{26}\)，\(\frac{5}{26}\)。按确定选择法，选择进入交换集的染色体串及其适应度情况如下表所示。

序号	染色体	适应度
1	0110	6
2	1100	12
3	1100	12
4	0101	5
适应度总和	-	35
最坏适应度	-	5
最好适应度	-	12
平均适应度	-	8.75

由上表可知，选择操作的作用是改进了\(OIer\)们的平均实力，使其由原来的\(6.5\)提高到了\(8.75\)，最坏适应度由原来的\(3\)改进为\(5\)，实力最差的蒟蒻已从种群中删除。但是，选择不能创造新的染色体，须进行交♂换操作。

交换操作

设采用单点交换，随机产生的交换点是\(2\)，从交换集中任取一对染色体\(1100\)和\(0101\)，互换它们的第\(3，4\)位，得子孙染色体串\(1101\)和\(0100\)。
如下图所示：

序号	染色体	适应度
1	0110	6
2	1100	12
3	1101	13
4	0100	4
适应度总和	-	35
最坏适应度	-	4
最好适应度	-	13
平均适应度	-	8.75

由上表可知，在新一代种群中，最强\(OIer\)实力由原来\(12\)提高到了\(13\)，其对应的二进制串是\(1101\)，已经非常接近\(IOI\)金牌水平了。平均适应度由原来的\(6.5\)提高到\(8.75\)，整个种群的适应度从总体上提高了，被优化了。
（以上例子取自\(2002\)年国家集训队论文《遗传算法的特点及其应用》）

总结

遗传算法多用于解决一类最优解问题。经典的有子集和问题与\(TSP\)问题。在这些\(NPC\)问题上，遗传算法都能发挥出很不错的效果。
遗传算法解决子集和问题：https://www.cnblogs.com/AKMer/p/9487269.html。
遗传算法解决\(TSP\)问题：https://www.cnblogs.com/AKMer/p/9496777.html。
至此，遗传算法的学习便结束了。因为是近似算法，所以只能在比赛中起到骗分作用，\(OJ\)上的题目是不可能\(AC\)的。大家只要会思想会写代码，自己设计出不错的估价函数即可获得贼高的部分分了。
祝你们欧洲旅行愉快哦！