浅谈树分治

因为树具有一般的图没有的特殊性质，所以树考的比图要多得多。而树上分治算法则是解决树上路径信息静态统计的一大利器。

点分治

以点为分界线的分治，每次选取一个点，把经过这个点的路径信息统计完，再在这个点的子树里递归统计没有经过这个点的路径信息，这样可以保证不重不漏的统计每一条路径的信息。如果每次选择重心为这个分界线，那么每次联通块大小至少会缩小一半，所以每个点最多被遍历\(logn\)次，复杂度就得到了保证。而当前联通块的重心只需要\(O(n)\)的时间就可以找到了。

边分治

树可以用点分治，当然也可以按边分治。每次选取一条边，使得删掉这条边之后的两个联通块大小尽量平均，暂时称这条边为重边。因为按照边分治每次只会把一个联通块变成两个，所以对于某些信息边分治比点分治更好统计。

但是，菊花图会卡爆上述做法。所以边分治之前，需要把树重建。在讲重建树之前，我们先来讲讲边分治的时间复杂度分析吧。

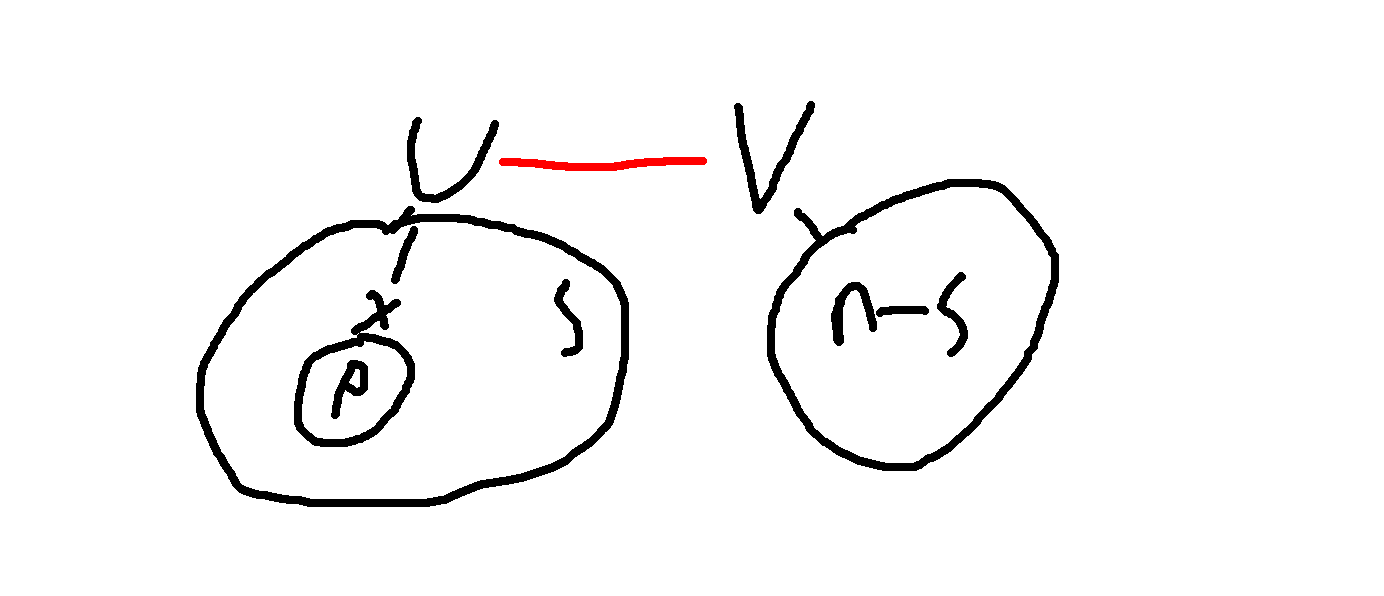
假设当前联通块中，红色的边\(U-V\)是重边，\(U\)以及其子树大小为\(s\)，\(V\)以及其子树大小为\(n-s\)。\(s\geqslant n-s\)。\(X\)是\(U\)的所有儿子中子树大小最大的点，其子树大小为\(p\)，整个联通块中点度最大为\(d\)。

我们考虑另一种方案\(U-X\)，显然\(p\geqslant (s-1)/(d-1)\)，因为\(p\)小于\(s\)且\(U-V\)是重边，所以\(n-p\geqslant s\)。代入前面那个式子可得：

\[\because n-p\geqslant s,\therefore n-s\geqslant p\\ \because p\geqslant (s-1)/(d-1),\therefore n-s\geqslant(s-1)/(d-1)\\ \therefore d*n-d*s-n+s\geqslant s-1\\ \therefore (d-1)*n-d*s\geqslant -1\\ \therefore (d-1)*n+1\geqslant d*s\\ \therefore s\leqslant \frac{(d-1)*n+1}{d}\\ \]

当\(d\)是常数时，复杂度显然可以接受。但是……

一花一世界，一菊一\(TLE\)。

所以我们需要重建树，利用虚拟结点和原本并不存在的边把原树建成一棵二叉树，内存也就翻一倍。另外，新的结点和新的边不能对答案有影响，这个在处理的时候要注意。