bzoj4237: 稻草人

这题不怎么好想，但想法挺好的。%%%PoPoQQQ，不会做就去%题解，结果看不懂，只能舍弃题解自己写了，写着写着……就做出来了。。。长得极其猥琐而且和题解做法好像不一样。。。所以说不要轻易%题解
好像最近做题都不能很快A，每次都要写对拍调小数据。。。

------------------瞎比比------------------------

这道题一开始肯定想的就是一个二维偏序咯，只要x[j]<=x[i]&&y[j]<=y[i]就满足形成田地第一个条件，主要就是判断田地之间有没有其他点是重点。

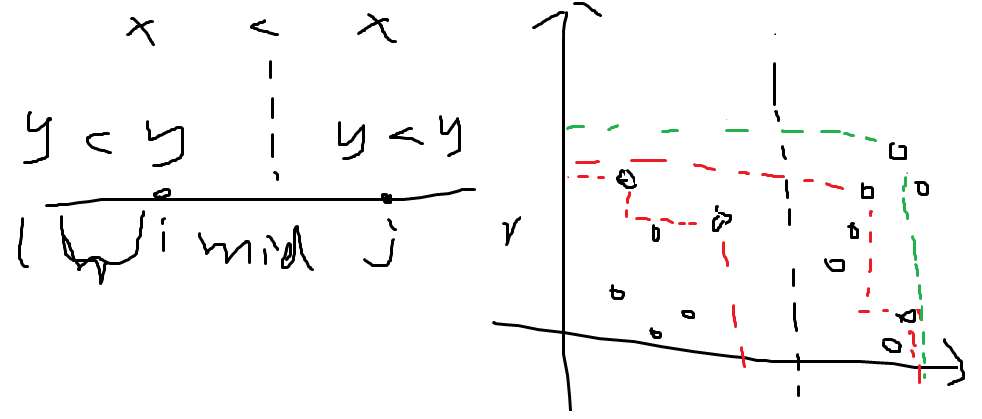
先注意一下，对于当前的cdq，左边整体的x坐标<右边的，并且左右两边的区间中y坐标分别按小到大排序了。

那我们不如换一种思维方式，对于一个点，可以视作在坐标轴上，以原点到该点形成的矩形被其覆盖，里面所有的点都不能再和其他的点形成田地。那么cdq肯定是左边更新右边的，对于左边的区间，我维护一个x坐标单调递减的栈，又因为分治的性质，我可以知道y是单调递增的，想象一下，这些点以及他们和坐标轴形成的矩形就像一个左高右低的楼梯，在楼梯左下边的点都不能被更新，而且，楼梯右上方绝对没有点，反证一下，假如有，那么这个点进入的时候更加应该成为楼梯的一部分，那么，左边所有可以用来更新右边的点，就在这个楼梯的边上！

那么是不是每次sum就+=top就可以了？？不，还有右边对答案的影响。这是一个很恶心的东西，有两个点很烦人：1、是右边也有x[j]<=x[i]&&y[j]<=y[i]的情况，那么j也应该计入我们的楼梯里面，但是j和左边无关，也就是保证不了y的顺序。2、因为右边只有y有序而x无序，有可能前面的一个点比当前的x坐标大，那这个点对于当前点的答案是没有影响的。

所以就要对于右边再维护一个单调栈，但是是按照x坐标递增，why？因为右边的x坐标一定比左边的大，所要考虑的是当前这个点的x坐标与前面的点的x坐标，如果前面的点x坐标大于当前就不取，这样的话就可以在栈里面二分求当前这个点x坐标的前驱，这个前驱就是右边能够给这个点造成影响的点了，而且是唯一的，因为它x最近当前点，y小于当前点，而那些y比它大的前面插入的点都不能影响到当前点。最后在左边二分一下这个前驱的y坐标的后继，就用楼梯把两边连在一起了，答案就是左边楼梯上的点数。

 

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;

struct node
{
    int x,y;
}a[210000];
bool cmp(node n1,node n2){return n1.x<n2.x;}

node t[210000];
int top1,sta1[210000],top2,sta2[210000];
LL sum;
int fhj(node k)
{
    if(k.x==-1)return 1;
    if(top1==0||a[sta1[top1]].y<k.y)return top1+1;
    
    int l=1,r=top1,ret;
    while(l<=r)
    {
        int mid=(l+r)/2;
        if(a[sta1[mid]].y<k.y)l=mid+1;
        else r=mid-1, ret=mid;
    }
    return ret;
}
node fqq(node k)
{
    if(top2==0||a[sta2[1]].x>k.x){node tt;tt.x=-1;return tt;}
    
    int l=1,r=top2;node ret;
    while(l<=r)
    {
        int mid=(l+r)/2;
        if(a[sta2[mid]].x>k.x)r=mid-1;
        else l=mid+1, ret=a[sta2[mid]];
    }
    return ret;
}
void cdq(int l,int r)
{
    if(l==r)return ;
    
    int mid=(l+r)/2;
    cdq(l,mid);
    cdq(mid+1,r);
    
    top1=0;top2=0;
    int i=l,j=mid+1,p=l;
    while(i<=mid&&j<=r)
    {
        if(a[i].y<a[j].y)
        {
            while(top1!=0&&a[sta1[top1]].x<a[i].x)top1--;
            sta1[++top1]=i;
            t[p++]=a[i++];
        }
        else
        {
            sum+=(top1-fhj( fqq(a[j]) )+1);
                
            while(top2!=0&&a[sta2[top2]].x>a[j].x)top2--;
            sta2[++top2]=j;
            t[p++]=a[j++];
        }
    }
    while(i<=mid)t[p++]=a[i++];
    while(j<=r)
    {
        sum+=(top1-fhj( fqq(a[j]) )+1);
            
        while(top2!=0&&a[sta2[top2]].x>a[j].x)top2--;
        sta2[++top2]=j;
        t[p++]=a[j++];
    }
    
    for(int i=l;i<=r;i++)a[i]=t[i];
}
int main()
{
//    freopen("dcr.in","r",stdin);
//    freopen("dcr1.out","w",stdout);
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&a[i].x,&a[i].y);
    sort(a+1,a+n+1,cmp);

    sum=0;
    cdq(1,n);
    printf("%lld\n",sum);
    return 0;
}