bzoj1492: [NOI2007]货币兑换Cash
码了我两个星期的题啊,终于写完了,感觉一半的时间都在调splay,后面写cdq好像轻松一点,cdq码量小一倍,而且又好想(可能是我调的时候理解了)感觉这种黑科技很nb,关键是可以减少细节出错(像我这种大头虾的福音)能写搜索谁写splay在线搞啊。
----------完结撒花!!-----------------------
1D1D动态规划问题。网上的大多都说有三类,然而我觉得吧,主要就是两类,一类利用单调性和斜率优化可以解决的,主要是因为能证明单调性(斜率与二元组的横坐标同时满足单调性,假如斜率不满足还可以在单调队列里二分,实际上很多时候都不用列二元组,你搞斜率优化的时候总看得出来吧)
拿这道题为例:
f[i]=max(f[i-1],sigema(1~i-1)j a[i] * f[j]/(a[j]*r[j]+b[j])*r[j] + b[i] * f[j]/(a[j]*r[j]+b[j]) );
只看后面:设X(i)=f[j]/(a[j]*r[j]+b[j])*r[j],Y(i)=f[j]/(a[j]*r[j]+b[j])
f[i]=max(a[i]*X[j]+b[i]*Y[j]), 由于X、Y可以得到,那么就在坐标系里表示
可以看作y=-a[i]*x/b[i]+f[i]/b[i]; 所以f[i]/b[i]越大f[i]越大
这个值就是y=kx+b里的b(纵截距) 这个询问的斜率k就是a[i]/b[i]
假如继承前面的一个点j,那么j的坐标肯定满足y=a[i]*x/b[i]+f[i]/b[i]
那就用一点和斜率确定一条直线,并且要令纵截距最大
先扯一些前提技能(让我画个图啊):
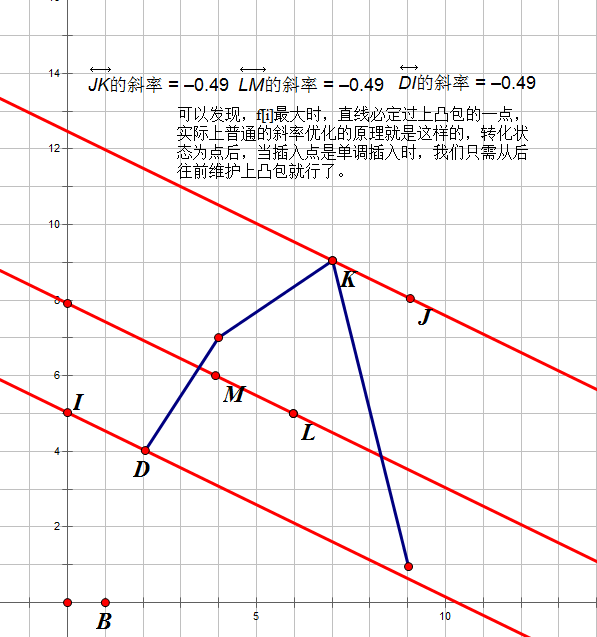
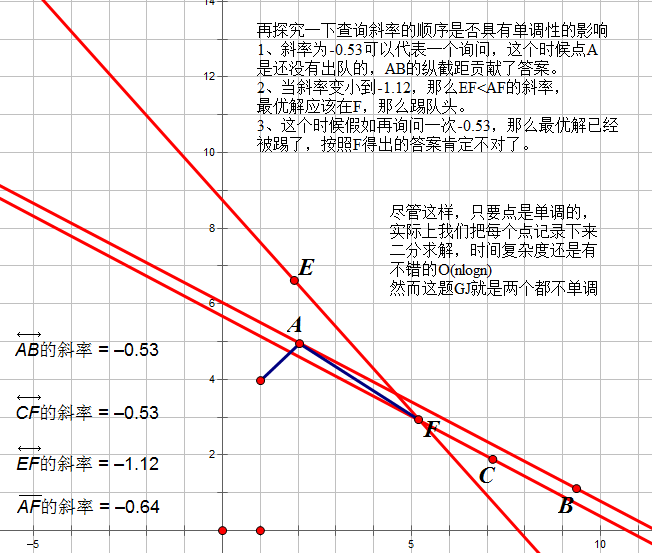
是了,那怎么办,有两个方法,一个是用splay,一个是用cdq分治。
1、splay
splay维护点,按照x坐标左大右小,每个节点保存和左右边的点的斜率(注意这个保存的不是左右孩子,而应该是在图上相邻的点),然后斜率也是单调的。
举个例子啊~ 很容易就可以看出,当lk>k>rk的时候,直线切凸包,然后呢这个点就是答案。
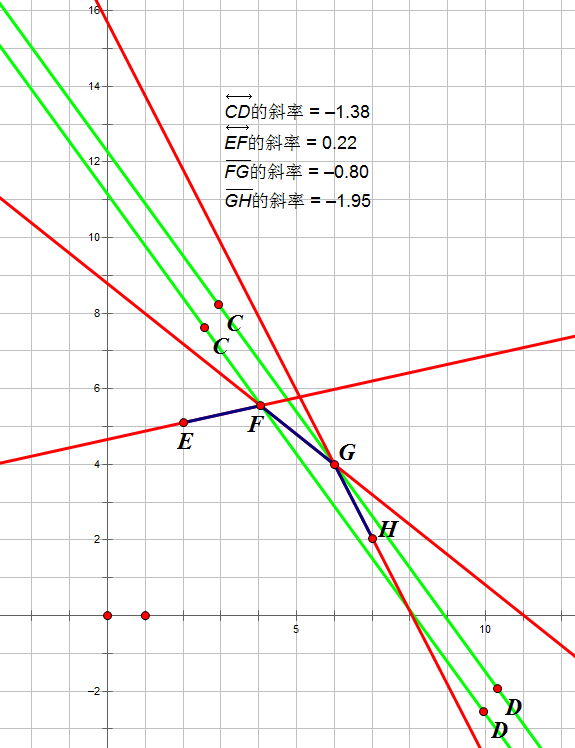
然后还有维护的问题,插入点的时候,有两种情况,一种是插入的点在凸包里面,那就不插入(这个就不举例子了,自己YY怎么判吧)
另外一种就是插入的点在凸包外,就像这样↓
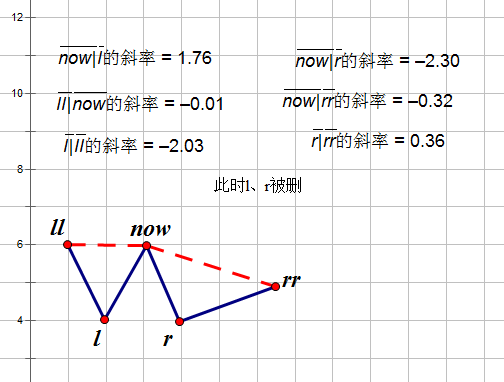
所以就要往左往右去debug,但是要注意边界的问题,可以注意到斜率不单调了,以此为判定。
很想骂一波bzoj的老爷机,他给我的数据就是我的数据的前80%,然后我的数据全过,有的AC代码RE了我的数据
2、cdq分治。
这题跟我以往做的不大一样啊。前面那题陌上花开,我是把两边都先递归了,然后在对右边的询问进行维护。但是这题的点跟f的值有关,也就是意味着,前面的点必须得到一个解才有可能更新后面的,并且如果前面的点得到的并不是最优解,还有可能要重新更新。
说白了就是一句话:如果不告诉我是cdq,鬼才会想到。
理一下思路。
既然要用cdq做,那我知道cdq是化再线为离线,并且我知道cdq可以用来排三维的序(好像不是这么说的),那就找找有什么要排序的?
1、很显然每个问的斜率 2、每个点的x坐标?因为要做的时候凸包上的点的x坐标都要单调上升 OK,加上问的顺序正好。
等等!x我得不出来啊。。
倏忽依稀记得有的大牛的cdq模版是这样的:把左边的分治完成;把左边的对右边答案的影响给到右边;把右边的分治完成。
而我的是这样的:把左边的分治完成;把右边的分治完成;把左边的对右边答案的影响给到右边;
这种顺序的差异有什么不同?大牛的cdq开始递归右边的时候,左边的答案已经出来了,尽管除了mid+1以外其他的都不一定是最优。但是,递归肯定先找到的是mid+1一边,然后又可以释放影响,这样后面的解就没有问题了。
而我以前的做法可能更多的是面对那些可以把中间一截看成独立的子问题的题,再将一个个子问题合并,最终得解。
于是乎我就飞快码代码了,这次连树状数组都没有用上,第二维排序按x坐标排就行了。至于左边的影响,肯定左边得到的是一个凸包,那么只要把它勾勒出来(有点感性),然后按照斜率的大到小顺序扫一遍(这个感觉就很像斜率优化那玩意了,但是假如直接在原数组里面按斜率归并然后还原肯定会错,因为原数组mid两边本来就不是按斜率而是按x坐标排的),结果我直接新定义了一个一毛一样的数组,专门用来排斜率,但是仍然WA,就是一脸懵逼,lj就跑去%了一发题解了。
结果看到code是先把斜率全局排了一次序,然后出乎意料,按问的顺序还原!?心中一万只cnm飞过,稳住。。
重新想一想,我的目标是什么?当左边的影响释放的时候,我要保证,右边的部分是按照斜率排序的。
假如简单粗暴的直接在递归中归并排斜率,在这个时间点,左边的部分是按照斜率排序,但是右边的仍然是像一开始的询问顺序排序,正好和要求相反了!
那假如我反过来,在递归中归并按询问顺序排,在这个时间点,岂不是(偷↗税↘)搞定了!?
错!
假如在分治之前按插入的时间先归并了一次,那么当前数组里l~r都是按照时间排的,感性的理解一下,左右的两块会混在一起。
那假如在分治之后在做呢?好像这样就没什么问题了?还记得一开始的DP方程?咩关系我告诉你:f[i]=max(f[i-1],sigema(1~i-1)j a[i] * f[j]/(a[j]*r[j]+b[j])*r[j] + b[i] * f[j]/(a[j]*r[j]+b[j]) );那么我们必须保证,最后搜到底层的时候,f[Q[i].t-1]一定要得出来并且一定得是最优解,那很容易发现分治之后归并,第一次搜索就出问题了,就是求f[Q[1].t-1]的时候(t表示这是第几个询问,因为cdq打乱了一开始的顺序),肯定这个时候的t应该要等于1,不然就继承不了f[0]了,一开始按斜率排序并不一定第一个询问斜率最大。
说了这么多,那么实际上还原具体怎么做?
对于当前,开始全局排过一次序以后,l~r一定是按照斜率排序的,然后我们把l~r中t<mid的按顺序放在前面l~mid的个格子里,把t>mid的放在mid+1~r的格子里,那么l~mid就是按斜率排的了,mid+1~r也是按斜率排的了,也就是相当于把两个分开。那么对于开始的要求,右边的部分是按照斜率排序的,就解决了,同时只要一步一步还原,到最后还原序列就是按时间排的,那么前面那个搜到底层的隐患就没有了。
终于写完了,两个星期的心血啊,肯定是我写的最长的blog了。
/* O(n^2)暴力DP,f表示这天有多少人民币,转移时就转换成券来求 A表示A券价值,B表示B券价值,S表示这个券的数量 题意得:A*Sa+B*Sb=F,Sa/Sb=R (A*R+B)*Sb=F; Sb=F/(A*R+B); Sa=Sb*R; */ #include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; double a[110000],b[110000],r[110000],f[110000]; int main() { int n; memset(f,0,sizeof(f)); scanf("%d%lf",&n,&f[0]); for(int i=1;i<=n;i++) { scanf("%lf%lf%lf",&a[i],&b[i],&r[i]); f[i]=f[i-1]; for(int j=i-1;j>=1;j--) { //劵->钱 double Sa,Sb;//劵数 Sb=f[j]/(a[j]*r[j]+b[j]); Sa=Sb*r[j]; f[i]=max(f[i],a[i]*Sa+b[i]*Sb); } } printf("%.3lf\n",f[n]); return 0; }
splay
/* 玄学bzoj数据,官方数据本机1.8s跑过提交TLE,其他也是跑1.8s的splay提交1s */ #include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; const double inf=1e11; const double eps=0e-8; double a[110000],b[110000],r[110000],f[110000]; //double x[110000],y[110000]; double poiX(int j){return f[j]/(a[j]*r[j]+b[j])*r[j];} double poiY(int j){return f[j]/(a[j]*r[j]+b[j]);} struct node { double x,y,lk,rk; int f,l,r,son[2]; }tr[110000];int len,root; double slope(node n1,node n2) { if(n1.y==-1) { if(fabs(n1.x)<=eps)return inf; else return -inf; } if(n2.y==-1) { if(fabs(n2.x)<=eps)return inf; else return -inf; } return (n1.y-n2.y)/(n1.x-n2.x); } void rotate(int x,int w) { int f=tr[x].f,ff=tr[f].f; int R,r; R=f;r=tr[x].son[w]; tr[R].son[1-w]=r; if(r!=0)tr[r].f=R; R=ff;r=x; if(tr[R].son[0]==f)tr[R].son[0]=r; else if(tr[R].son[1]==f)tr[R].son[1]=r; tr[r].f=R; R=x;r=f; tr[R].son[w]=r; tr[r].f=R; } void splay(int x,int rt) { while(tr[x].f!=rt) { int f=tr[x].f,ff=tr[f].f; if(ff==rt) { if(tr[f].son[0]==x)rotate(x,1); else if(tr[f].son[1]==x)rotate(x,0); } else { if(tr[ff].son[0]==f&&tr[f].son[0]==x){rotate(f,1);rotate(x,1);} else if(tr[ff].son[1]==f&&tr[f].son[1]==x){rotate(f,0);rotate(x,0);} else if(tr[ff].son[0]==f&&tr[f].son[1]==x){rotate(x,0);rotate(x,1);} else if(tr[ff].son[1]==f&&tr[f].son[0]==x){rotate(x,1);rotate(x,0);} } } if(rt==0)root=x; } //---------splay内部操作------------------------ double findmax(int i,double k) { /* double ss=0; for(int j=3;j<=len;j++) { if(tr[tr[j].f].son[0]==j||tr[tr[j].f].son[1]==j||tr[j].f==0) ss=max(ss,a[i]*tr[j].x+b[i]*tr[j].y); } return ss;*/ int now=root; while(now!=0) { int lc=tr[now].son[0],rc=tr[now].son[1]; if(tr[now].lk<k&&tr[now].rk<k)now=lc; else if(tr[now].lk>k&&tr[now].rk>k)now=rc; else return a[i]*tr[now].x+b[i]*tr[now].y; } } int findqianqu(double x) { int now=root,ret=-1; while(now!=0) { if(tr[now].x<x) { ret=now; now=tr[now].son[1]; } else now=tr[now].son[0]; } return ret; } int findhouji(double x) { int now=root,ret=-1; while(now!=0) { if(tr[now].x>x) { ret=now; now=tr[now].son[0]; } else now=tr[now].son[1]; } return ret; } //--------------find---------------------- void del(int dl,int dr) { if(tr[dl].x>tr[dr].x)return ; int l=findqianqu(tr[dl].x),r=findhouji(tr[dr].x); splay(l,0);splay(r,l); tr[r].son[0]=0; } void debug(int now) { int L,R; int l=tr[now].l,ll=tr[l].l; L=now;R=l; while(ll!=1&&ll!=0) { double sp=slope(tr[ll],tr[now]);//决定l是否删 if(sp>tr[l].lk&&sp<tr[l].rk) { tr[len].l=ll;tr[ll].r=len; tr[len].lk=tr[ll].rk=slope(tr[ll],tr[len]); L=l, l=ll, ll=tr[l].l; } else break; } del(L,R); int r=tr[now].r,rr=tr[r].r; L=r;R=now; while(rr!=2&&rr!=0) { double sp=slope(tr[now],tr[rr]); if(sp>tr[r].lk&&sp<tr[r].rk) { tr[len].r=rr;tr[rr].l=len; tr[len].rk=tr[rr].lk=slope(tr[len],tr[rr]); R=r, r=rr, rr=tr[r].r; } else break; } del(L,R); } //-------------debug---------------------- void add(int i,int f) { len++; tr[len].x=poiX(i);tr[len].y=poiY(i); tr[len].f=f;tr[len].son[0]=tr[len].son[1]=0; tr[f].son[0]=len; } void ins(int i) { node tno; tno.x=poiX(i);tno.y=poiY(i); int L=findqianqu(poiX(i)); int R=findhouji (poiX(i)); double sp=tr[L].rk; double spl=slope(tr[L],tno),spr=slope(tno,tr[R]); if(L==1||R==2||(spl>sp&&sp>spr)) { splay(L,0);splay(R,L);add(i,R); tr[len].l=L;tr[len].r=R; tr[L].r=len;tr[R].l=len; tr[len].lk=tr[L].rk=slope(tr[L],tr[len]); tr[len].rk=tr[R].lk=slope(tr[len],tr[R]); splay(len,0);debug(len);splay(len,0); } } //----------splay外部操作------------ void yu() { len=root=3; tr[1].x=0.0;tr[1].y=-1;tr[1].f=3;tr[1].l=tr[1].r=0; tr[2].x=inf;tr[2].y=-1;tr[2].f=3;tr[2].l=tr[2].r=0; tr[1].r=len;tr[2].l=len; tr[1].son[0]=tr[1].son[1]=0; tr[2].son[0]=tr[2].son[1]=0; tr[1].lk=inf, tr[2].rk=-inf; tr[3].x=poiX(1);tr[3].y=poiY(1);tr[3].f=0; tr[3].l=1;tr[3].r=2; tr[3].son[0]=1;tr[3].son[1]=2; tr[3].lk=tr[1].rk=slope(tr[1],tr[3]); tr[3].rk=tr[2].lk=slope(tr[3],tr[2]); } /* int tt[11000],tlen; void dfs(int x) { if(tr[x].son[0]!=0)dfs(tr[x].son[0]); tt[++tlen]=x; if(tr[x].son[1]!=0)dfs(tr[x].son[1]); } */ int main() { //freopen("cash.in","r",stdin); //freopen("cash.out","w",stdout); int n; memset(f,0,sizeof(f)); scanf("%d%lf",&n,&f[0]);f[1]=f[0]; for(int i=1;i<=n;i++) scanf("%lf%lf%lf",&a[i],&b[i],&r[i]); yu(); //x[1]=poiX(1);y[1]=poiY(1); for(int i=2;i<=n;i++) { f[i]=max( f[i-1],findmax(i,-a[i]/b[i]) ); // x[i]=poiX(i);y[i]=poiY(i); ins(i); /* double ss=0; for(int j=3;j<=len;j++) if(tr[tr[j].f].son[0]==j||tr[tr[j].f].son[1]==j||tr[j].f==0) if(tr[j].lk<tr[j].rk){printf("%d\n",i);return 0;}*/ /* tlen=0;dfs(root); for(int j=1;j<=tlen;j++)printf("%d ",tt[j]); printf("\n");*/ } // for(int i=1;i<=n;i++)printf("%.3lf\n",f[i]); printf("%.3lf\n",f[n]); return 0; }
cdq
#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; const double inf=-2147483647.0; const double eps=1e-8; struct query { int t; double a,b,r,sp; }Q[110000]; bool cmp(query a,query b){return a.sp>b.sp;} struct point { double x,y; }P[110000]; double slope(int i,int j) { if(fabs(P[i].x-P[j].x)<=eps)return -inf; return (P[i].y-P[j].y)/(P[i].x-P[j].x); } //----------------------------------- double f[110000]; int top,sta[110000]; void solve(int l,int r) { int mid=(l+r)/2; top=0; for(int i=l;i<=mid;i++)//形成凸包 { while(top>1&&slope(sta[top-1],sta[top])<slope(sta[top],i))top--; sta[++top]=i; } int p=1; for(int i=mid+1;i<=r;i++) { while(p<top&&slope(sta[p],sta[p+1])>Q[i].sp)p++; f[Q[i].t]=max(f[Q[i].t],P[sta[p]].x*Q[i].a+P[sta[p]].y*Q[i].b); } } query t1[110000];point t2[110000]; void cdq(int l,int r) { if(l==r) { f[Q[l].t]=max(f[Q[l].t-1],f[Q[l].t]); P[l].x=f[Q[l].t]/(Q[l].a*Q[l].r+Q[l].b)*Q[l].r; P[l].y=f[Q[l].t]/(Q[l].a*Q[l].r+Q[l].b); return ; } int mid=(l+r)/2,i,j,p; //!!!! i=l,j=mid+1,p=l; while(p<=r) { if(Q[p].t<=mid)t1[i++]=Q[p]; else t1[j++]=Q[p]; p++; } for(int i=l;i<=r;i++)Q[i]=t1[i]; cdq(l,mid); solve(l,r); cdq(mid+1,r); i=l,j=mid+1,p=l; while(i<=mid&&j<=r) { if(P[i].x<P[j].x)t2[p++]=P[i++]; else t2[p++]=P[j++]; } while(i<=mid)t2[p++]=P[i++]; while(j<=r) t2[p++]=P[j++]; for(int i=l;i<=r;i++)P[i]=t2[i]; } int main() { // freopen("cash.in","r",stdin); // freopen("cash.out","w",stdout); int n; scanf("%d%lf",&n,&f[0]); for(int i=1;i<=n;i++) { scanf("%lf%lf%lf",&Q[i].a,&Q[i].b,&Q[i].r); Q[i].sp=-Q[i].a/Q[i].b;Q[i].t=i; } sort(Q+1,Q+n+1,cmp); cdq(1,n); printf("%.3lf\n",f[n]); return 0; }

