bzoj2286: [Sdoi2011]消耗战

估计像我一样想树形DP搞搞不想时间复杂度的蒟蒻很少见了~~~~

然而花了一个下午学会了——虚树！！！厉害！（感觉在竞赛室都在不停的get新姿势，舒服）

这个东西呢主要是省略一些不会访问到的点。比如这题的样例第一个问，我们就把树变成这样：

 

就是保留根，通过保留lca和要断的节点来把树的形状得出。

具体的做法，就是弄一个单调栈，栈头到栈尾由浅至深↓

 

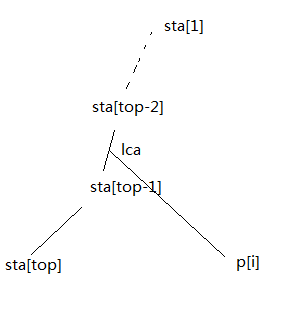
然后，找到lca，如图，那我们这时就可以将sta[top]和sta[top-1]的边建好，然后踢栈顶，接着让新的sta[top]和lca的边建好，然后将lca和p[i]进栈，最后得到的就是虚树了。

 

细节：如果在while里面每次都重置一遍elast，时间就还是O(nm)，所以就要在DP的时候顺便清空，还有inf要开大。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
LL inf;
int Bin[25];
struct node
{
    int x,y,d,next;
}a[510000],e[510000];int len,last[310000],elen,elast[310000];
void ins(int x,int y,int dd)
{
    len++;
    a[len].x=x;a[len].y=y;a[len].d=dd;
    a[len].next=last[x];last[x]=len;
}
void ins2(int x,int y)
{
    elen++;
    e[elen].x=x;e[elen].y=y;
    e[elen].next=elast[x];elast[x]=elen;
}
int cnt,pos[310000];
LL v[310000];
int dep[310000],f[25][310000];
void dfs(int x,int fa)
{
    pos[x]=++cnt;
    f[0][x]=fa;
    for(int i=1;Bin[i]<=dep[x];i++)f[i][x]=f[i-1][f[i-1][x]];
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(y!=fa)
        {
            if(v[x]<a[k].d)v[y]=v[x];
            else v[y]=a[k].d;
            
            dep[y]=dep[x]+1;
            dfs(y,x);
        }
    }
}
int LCA(int x,int y)
{
    if(dep[x]<dep[y])swap(x,y);
    
    for(int i=20;i>=0;i--)
        if(dep[x]-dep[y]>=Bin[i])x=f[i][x];
    if(x==y)return x;
    
    for(int i=20;i>=0;i--)
        if(dep[x]>=Bin[i]&&f[i][x]!=f[i][y]){x=f[i][x];y=f[i][y];}
    return f[0][x];
}
bool cmp(int n1,int n2)
{
    if(pos[n1]<pos[n2])return true;
    return false;
}
int k,p[310000];
int top,sta[310000];//sta表示在已经建完毕的虚树上,以最后一个插入的点为端点的DFS链
void virtual_tree()
{
    sort(p+1,p+k+1,cmp);
    //按dfs序大到小排序，对于任意点，dfs序大于该点值的点要么处于它的子树中，要么在另一棵同级的子树 
    int tp=1;//如果p[i]是处于p[tp]的子树里，只要p[tp]断了，p[i]同样断，so无视 
    for(int i=2;i<=k;i++)
        if(LCA(p[i],p[tp])!=p[tp])p[++tp]=p[i];
    k=tp;
        
    top=0;sta[++top]=1;
    for(int i=1;i<=k;i++)
    {
        int lca=LCA(p[i],sta[top]);
        while(1)//不停往上跳令dep[sta[top]]>dep[lca]>dep[sta[top-1]]
        {
            if(dep[lca]>=dep[sta[top-1]])//找到 
            {
                if(lca!=sta[top])ins2(lca,sta[top]);//下面的连向lca，然后没用了 
                top--;
                if(lca!=sta[top])sta[++top]=lca; 
                break;
            }
            ins2(sta[top-1],sta[top]);top--;//往上跳时顺便将下面的连在一起 
        }
        if(p[i]!=sta[top])sta[++top]=p[i];
    }
    top--;
    while(top>0){ins2(sta[top],sta[top+1]);top--;}
}
LL dp[310000];
void treeDP(int x)
{
    LL ans=0;dp[x]=v[x];
    for(int k=elast[x];k;k=e[k].next)
    {
        int y=e[k].y;
        treeDP(y);
        ans+=dp[y];
    }
    elast[x]=0;
    if(ans!=0)dp[x]=min(dp[x],ans);
}
int main()
{
    //freopen("repair.in","r",stdin);
    //freopen("repair.out","w",stdout);
    
    inf=1;for(int i=1;i<=60;i++)inf*=2;
    Bin[0]=1;for(int i=1;i<=25;i++)Bin[i]=Bin[i-1]*2;
    
    int n,x,y,dd;
    scanf("%d",&n);
    len=0;memset(last,0,sizeof(last));
    for(int i=1;i<n;i++)
    {
        scanf("%d%d%d",&x,&y,&dd);
        ins(x,y,dd);ins(y,x,dd);
    }
    cnt=0;dep[1]=1;v[1]=inf;dfs(1,0);
    
    int m;
    scanf("%d",&m);
    while(m--)
    {
        scanf("%d",&k);
        for(int i=1;i<=k;i++)scanf("%d",&p[i]);
        elen=0;
        virtual_tree();
        treeDP(1); 
        printf("%lld\n",dp[1]);
    }
    return 0;
}