623


当时写第一道题时, 只想到了40分的做法, 就是枚举每一种情况, 最后check一遍, 时间复杂度应该是(n * !n), 最后看了题解, 是一道树形dp, f[i][0] 表示不选第i个节点, f[i][1]表示选i节点, 则显然有
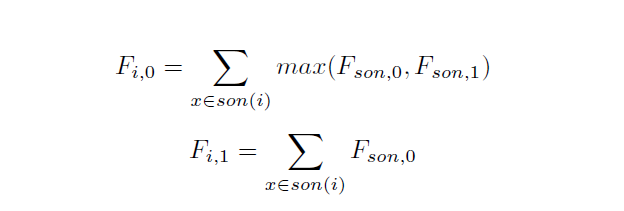
用邻接表就能做到O(n) 的时空复杂度。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int INF = 0x3f3f3f3f; const int MAXN = 5e5 + 100; const int MAXM = 3e3 + 10; const double eps = 1e-5; template < typename T > inline void read(T &x) { x = 0; T ff = 1, ch = getchar(); while(!isdigit(ch)) { if(ch == '-') ff = -1; ch = getchar(); } while(isdigit(ch)) { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } x *= ff; } template < typename T > inline void write(T x) { if(x < 0) putchar('-'), x = -x; if(x > 9) write(x / 10); putchar(x % 10 + '0'); } int n, lin[MAXN], tot = 0, ans, f[MAXN][2], vis[MAXN]; struct edge { int y, next; }e[MAXN]; inline void add(int xx, int yy) { e[++tot].y = yy; e[tot].next = lin[xx]; lin[xx] = tot; } void dfs(int x) { f[x][1] = 1, f[x][0] = 0; vis[x] = true; for(int i = lin[x], y; i; i = e[i].next) { if(vis[y = e[i].y]) continue; dfs(y); f[x][0] += max(f[y][0], f[y][1]); f[x][1] += f[y][0]; } } int main() { freopen("a.in", "r", stdin); freopen("a.out", "w", stdout); read(n); for(int i = 1; i < n; ++i) { int u, v; read(u); read(v); add(u, v); add(v, u); } dfs(1); ans = max(f[1][1], f[1][0]); write(ans); return 0; }

合并石子, 一个区间dp模板

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int INF = 0x3f3f3f3f; const int MAXN = 5e5 + 100; const int MAXM = 1e3 + 10; template < typename T > inline void read(T &x) { x = 0; T ff = 1, ch = getchar(); while(!isdigit(ch)) { if(ch == '-') ff = -1; ch = getchar(); } while(isdigit(ch)) { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } x *= ff; } template < typename T > inline void write(T x) { if(x < 0) putchar('-'), x = -x; if(x > 9) write(x / 10); putchar(x % 10 + '0'); } int n, ans, a[MAXM], sum[MAXM], f[MAXM][MAXM]; int main() { freopen("b.in", "r", stdin); freopen("b.out", "w", stdout); read(n); for(int i = 1; i <= n; ++i) { read(a[i]); sum[i] = sum[i - 1] + a[i]; } for(int i = n + 1; i <= 2 * n; ++i) { a[i] = a[i - n]; sum[i] = sum[i - 1] + a[i]; } for(int len = 2; len <= n; ++len) { for(int l = 1; l <= 2 * n - len + 1; ++l) { int r = l + len - 1; for(int i = l; i <= r; ++i) { f[l][r] = max(f[l][r], f[l][i] + f[i + 1][r]); } f[l][r] += sum[r] - sum[l - 1]; } } for(int i = 1; i <= n; ++i) { ans = max(ans, f[i][i + n - 1]); } write(ans); return 0; }

暴力很好想, 全排列再check一下,时间复杂度为(n * !n); 正解是状态压缩dp, 用二进制2n枚举所选的点, f[i][j] 表示当选取方案为i时, 以j结尾的方案数, 首先枚举每一种方案, 在枚举每个点j作为结尾, 如果该点在方案中, 则枚举能够与该点相邻的点k, 如果该相邻的点也在此方案中, 那么f[i][j] 就可以由f[i - (1 << j)][k] 更新过来, 即在i中将j这个点剔除, 再以k为节点的方案数, 最后将枚举所有点时, 即(1 <<n) - 1, 以所有点为结尾的方案相加, 就是最终答案;

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int INF = 0x3f3f3f3f; const int MAXN = 5e5 + 100; const int MAXM = 3e3 + 10; template < typename T > inline void read(T &x) { x = 0; T ff = 1, ch = getchar(); while(!isdigit(ch)) { if(ch == '-') ff = -1; ch = getchar(); } while(isdigit(ch)) { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } x *= ff; } template < typename T > inline void write(T x) { if(x < 0) putchar('-'), x = -x; if(x > 9) write(x / 10); putchar(x % 10 + '0'); } int n, k, a[MAXN]; vector < int > q[20]; ll ans, f[1 << 17][20]; int main() { freopen("c.in", "r", stdin); freopen("c.out", "w", stdout); read(n); read(k); for(int i = 0; i < n; ++i) { read(a[i]); f[1 << i][i] = 1; } for(int i = 0; i < n; ++i) { for(int j = i + 1; j < n; ++j) { if(abs(a[i] - a[j]) > k) { q[i].push_back(j); q[j].push_back(i); } } } for(int i = 0; i < 1 << n; ++i) { for(int j = 0; j < n; ++j) { if((i >> j) & 1) { for(int l = 0; l < q[j].size(); ++l) { if((i >> q[j][l]) & 1) { f[i][j] += f[i - (1 << j)][q[j][l]]; } } } } } for(int i = 0; i < n; ++i) { ans += f[(1 << n) - 1][i]; } write(ans); return 0; }


