网络流与图匹配

【学习笔记】网络流

(2024.4.23)

时代的眼泪，近几年真的有考过吗，感觉不如二分图。

Part1. 基本定义

1. 流函数 $f$ 满足 1.斜对称性 2.流量守恒。
2. 定义残量网络为容量函数 $c^{\prime }=c-f$ 的网络，当 $c^{\prime }=0$ 视作不存在。
3. 定义增广路 $P(V,E_f),$ 是残量网络上一条 $S\to T$ 的路径。
4. 定义割为将 $V$ 分成两个不相交集合 $A,B$ ，且 $S\in A,T\in B$ 。定义割的 容量 为 $\sum \sum c(u,v)$ ，流量为 $\sum \sum f(u,v)$ 。若 $u,v$ 所属集合不同，则边 $(u,v)$ 为割边。最小割即为将 容量 最小化的分割方案。

Part2. 最大流

定义一次 增广 操作为：找到残量网络上一条增广路，每一条边增加 $p=min{c}_f(u,v)$ 的流量。并将其反边 $(v,u)$ 的 容量 增加 $p$ ，这样做目的即支持反悔。

实现上，$cnt=1$ 开始，且先进行 ++cnt ，并且正反边 紧邻 ，则 i^1 即为反向边。即正向边是偶数，反向边是下一个奇数。

EK 算法

即使用 bfs 寻找 长度最短 的增广路，此时复杂度为 $O(n{m}^2)$ ，若任意选择，则复杂度退化为跟流量相关，即 可能会在两个点之间来回增广的 dfs 方法。

Dinic 算法

核心思想是 分层图 以及 当前弧优化 。分层图的目的是规范增广路的形态，避免形成一个环。

增广路时流量等于容量的满边是无用的，可以直接跳过，为此记录每个点出发第一条没有流满的边，称为 当前弧 ，看似是常数优化实际上影响了复杂度：不加优化为 $O(n{m}^2)$ ，加入当前弧优化为 $O(n^{2}m)$ 。

Part3. 无负环的费用流

相较于一般网络流，每条边加入一权值 $w(u,v)$ ，最小费用最大流需要在 保证最大流 基础上，使得 $\sum f(x,y)\times w(x,y)$ 最小。简单来说，$w(u,v)$ 就是每条边流 $1$ 的费用。

连续最短路 SSP 算法

实现上，将 Dinic 的 BFS 换做 SPFA，且 DFS 多路增广时，仅在 $d[x]+w=d[y]$ 的边上进行。注意实现上退流后费用也要退掉，因此反边权值为 $-w(x,y)$ 。

理论时间复杂度为 $O(nmf)$ ，但实际上远远达不到。

注意 SPFA 在队首位 T 时不能直接 break; ，因为此时 d[T] 不一定是最短路。

Part4. 最大流最小割定理

感性理解就是 最小割一定是 $A$ 全在左边，$B$ 全在右边，则此时取得最小割，也就是从中间切一刀，得到的所有流量之和，为最大流。

【模板】最小割树（Gomory-Hu Tree）

${10}^5$ 次询问一个图，$u,v$ 两点间的最小割。

定理：不管怎么选两点，最小割只有 $n-1$ 种。

因此考虑分治，每次在原图上找两个点 $u,v$ ，求完他们的最小割，在最小割树上连边 $(u,v)=\text{mincut}$，然后原图被分为两部分，再递归做即可。

结论：$u,v$ 的最小割，是两点在最小割树上的路径最小值。

然后对于多次询问，树上倍增处理即可。

但是，因为网络流的图都很小 $n\le 1000$ ，所以我们可以直接 $n^2$ 预处理所有询问，并且无需建树，树在心中。

Part5. 对网络流的理解

1. 费用流与贪心

   费用流的策略是找到长度短的增广路进行增广，并且在添加反边以支持返回。因此 费用流和反悔贪心可以相互转化，于是一些费用流题目，可以转换为贪心再方便地利用数据结构维护。

2. 费用流与凸性

   如果问题可以抽象成费用流模型，每一滴流量带来的贡献单调，则选取 $i$ 个物品答案 $f(i)$ 有凸性，可以使用 wqs二分。

3. 最小割求方案

   可能会理解割边为最大流上流满的边，反例：$S\to 1\to T$ 。

   正确的做法是，残量网络上 $S$ 能到达的点为 $A$ ，否则为 $B$ 。再判断割边。

4. 反悔的性质

   在解决 动态加边 的最大流问题时，不需要担心原来的流方案影响正确性，因为正确性基于反悔。

   但对于费用流问题，正确性基于最短路，则加入新边后需要重新跑 SPFA。

Part6. 上下界网络流

即新增下界 $b(u,v)$ ，需要满足 $b\le f\le c$ 。

1.无源汇可行流

可行性主要在于流量守恒，即每个点不能储存流量。

核心思想：先满足下界限制，在尝试调整 。具体地，先让每条边都流满下界 $b$ ，算出每个点净流量 $w=\sum f(u,i)-\sum f(i,u)$ 。需要满足每个点 $w=0$ 。

根据 斜对称性，则不妨设 $\mathrm{\Delta }=\sum _{w_i>0}{w}_i=\sum _{w_i<0}-w_i$ 。如果能将 $\mathrm{\Delta }$ 在满足上界前提下分配，则具有可行性。

这启发我们新建一个网络 $G^{\prime }=\{V,E^{\prime }=c-f=c-b\}$ ，然后建立虚拟源点汇点 $SS,TT$ ，若 $w_i>0$ ，则 $SS\to i$ 连容量为 $w_i$ 的边，否则，$i\to TT$ 连容量为 $-w_i$ 的边，不难发现流出 $SS$ 的容量和流进 $TT$ 的流量均为 $\mathrm{\Delta }$ 。若 $SS\to TT$ 的最大流等于 $\mathrm{\Delta }$ ，则 $f(u,v)=b(u,v)+f^{\prime }(u,v)$ 为合法方案。

---

这个地方特别容易记混，如果一个点入度大于出度，则应该由虚拟源点向其连边，因为这样才能让这个点多流出这些流量。

2. 有源汇可行流

从 $T\to S$ 连容量为下界为 $0$ ，上界为正无穷的边。由于流量守恒，则这条边的流量即为答案。

细节：最后加这条边，则直接删 e[tot].w 即可。

3. 有源汇最大流

引理：对于任意一组可行流，对其运行最大流算法，总能得到最大流。

因此，得到一组可行流 $G$ 后，新建网络 $G^{\prime }$ 为去掉 $SS,TT$ ，以及 $T\to S$ 容量为正无穷的边，则以 $S,T$ 为源汇点跑最大流，最后的答案是 可行流流量+新的最大流流量 ，且注意可行流流量为 $T\to S$ 的反边流量，而不是 $SS\to TT$ 的流量。

4. 有源汇费用流

同样转换即可，初始为 $\sum w(u,v)b(u,v)$ 。

Part7. 应用与模型

1. 最小割点----点边转化

将每个点拆为 $i_{in}$ 和 $i_{out}$ ，从 $i_{in}\to i_{out}$ 连 $w_i$ 的边，$u_{out}\to v_{in}$ 连 $inf$ 的边。因为我们只能删点，不能删边。

2. 集合划分模型

有 $n$ 个物品，$A,B$ 两个集合，分到两个集合的代价分别是 $a_i$ 和 $b_i$ ，给定若干限制 $(u,v,c_{u,v})$ 表示 $u,v$ 不在一个集合还需要付出的额外代价。代价最小是多少。

建模：将 $S\to i$ ，容量为 $b_i$ ，$i\to T$ ，容量为 $a_i$ ，$i,j$ 之间连双向边，容量为 $c_{i,j}$ 。此时问题显然等价于最小割。

扩展

• 若 $a,b$ 存在负值，则同时加上 $\delta$ ，最后结果减去 $\sum \delta$ ，因为每个点只有选或不选两种状态，所以与最短路等模型不同，其不会影响答案。

3. 最大权闭合子图

或许是更系统的理解方式。

有向图 的闭合子图是指 $G^{\prime }=\{V^{\prime },E\}$ ，也即选择一个点集，使得他们所有连边仍在闭合子图上。点有点权，求最大权值。

考虑转换为集合划分模型，若一个点选，则 $S$ 与 $i$ 相连，则要割掉 $i\to T_i$ ，故 $i\to T_i$ 容量为 $a_i$ ，对于原图上的一条边 $(u,v)$ ，则其必须都选，即容量为 $-\text{infin}$ 。

此时是最大割（NP-Hard）问题，转换成最小割， $a_i$ 变成负值，运用上文拓展，将 $S\to i$ 和 $i\to T$ 同时加上 $a_i$ ，这样就只有前者有值了。最后再减去 $\sum a_i$ 即可。

当然有的 $a_i$ 本身就是负数，那我们就不管他们了。最后记得取反变成最小割。

总结：原图建出来，每条边赋值 $+\text{infin}$ ，源点连正权点，负权点连汇点，最后再跑最小割 $x$ ，答案为 $(\sum _{a_i>0}{a}_i)-x$ 。

4. 有负环的费用流

运用上下界网络流将负权边强制满流即可，再建立 $(v,u)$ 用于回流。相当于再额外让一些负权边少流。

记录详情 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 。还是注意第一步最大流应该取 e[tot].w 的，并且要清空这条边的容量。

应用在哪？很多题的贪心可能是最大费用最大流之类的，取反后即为（可能）有负环的费用流。

Part8.（新）网络流二十四题

1. P1251 餐巾计划问题

每天需要 $r_i$ 条干净毛巾，用完后的脏毛巾可以有两种送洗方案： $m$ 天后用，费用 $f$ ，$n$ 天后用，费用 $t$ ，或者保存起来延期送洗。你同时可以选择买干净毛巾，价格 $s$ 。

此题精髓在于对两种毛巾状态的拆点处理。

我们可以想到，每天开始的时候只有干净的餐巾可使用，每天结束的时候仅有脏的餐巾需要操作。于是将每天拆成两个点：起始点与结束点，分别处理不同时间段所需操作。

起始点连向汇点，源点连向结束点，表示每天固定要用 $r_i$ 条。

对于一个起始点，有源点连向他表示购买毛巾。

对于一个结束点，连向 $m,n$ 天后的起始点表示送洗，连向 $i+1$ 天的结束点表示延期送洗。

Debug

费用流中，如果仅判断 dis，而不判断 dep ，应在开头判断是否为终点，否则在终点有边权为 $0$ 边时会死循环。

2. P2764 最小路径覆盖问题

求一张有向无环图，所有点都覆盖一次，路径最少的个数。

要求点只通过一次是困难的，这启发我们点边互换，套路的，将一个点拆为 $i_{in}$ 和 $i_{out}$ 。

我们考虑调整法，初始状态是 $n$ 条只有一个点的路径覆盖所有点，考虑合并两个路径，即为一个点的 $i_{out}\to j_{in}$ 。这一点流量说明减少一个路径，故 $n-$ 最大流就是答案。

3. P4043 [AHOI2014/JSOI2014] 支线剧情

给定一个 DAG，边有边权，有若干出度为 $0$ 的点和一个入度为 $0$ 的点 $1$ ，可以回退到根，求 到达所有叶子节点 的边权之和最小值。

相当于每条边下界为 $1$ 的最小费用可行流。

Debug

容易搞混虚拟源点汇点连边的方向。

4. P1646 [国家集训队] happiness

在集合 $A$ 价值为 $a$ ，在集合 $B$ 价值为 $b$ ，若干个同时在 $A/B$ 有价值 $c/d$ ，求最大价值。

集合划分问题模板，转换为最小割即可。

注意题目要求最大价值，且限制是两人在一个集合的额外价值。

用总答案减去最小割，转换为不选...的问题，对于相邻两个学生，则新建一个点 $x$ 连接他俩，容量为 $+\text{infin}$ ，表示不能割，$S\to x,x\to T$ 容量分别为 两个人同时不选择文/理的价值。

有若干倍经验均是此套路。

Debug

不是这太坑了，注意连边方向，别把虚拟点连成新的”源汇点“。评测记录 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

还有 id(x,y)=(x-1)*m+y 不要写成 n 呀。

flag：我就不信我今天还能连边方向出问题。

6. P5029 T'ill It's Over

初始有 $n$ 个数 $1$ ，你有 $m$ 次操作，每次操作可以将一个范围在 $[l,r]$ 的数变成 $[u,v]$ 的任意一个数，且这个操作有次数限制。

求最后最多有多少个数变成 $k$ 。

注意操作不是在线的。值域 ${10}^5$ 。

将值域抽象为点，则显然是网络最大流。

然后显然是线段树优化建图区间连区间，根据套路，两颗线段树，一颗向上连，一颗向下连，共用叶子。

还是线段树良心，一遍过了。记录详情 - 洛谷

7.CF1009G Allowed Letters

给你一个字符串 $s$ ，字符集为 $\{a,b,c,d,e,f\}$，你可以任意排列。需要保证每个位置的字符集为 $T$ 。问字典序最小是多少？$|s|\le {10}^5$ 。

对于字典序问题都可以贪心，对于每个位置枚举当前填 $c$ 是否合法，如何判断？因为有可能这里填了后面就不能再填了，关系抽象到图论上，形成一个二分图，我们只需检查有无完美匹配即可。

具体的，二分图左部是每个位置，右部是六个字符。一个位置 $p$ 对应一个字符集 $T_p$ ，则 $t\in T_p\to p,p\to s_p$ 连边即可。一组匹配相当于若干个交换，检查是否存在完美匹配。若检查成功，则删去这条边。

检查完美匹配，我们通常可以想到两个方法：增广路和 Hall 定理。增广路的做法就是走状压 dp 的套路。两者都适用于 $n$ 比较小的情况。

考虑 Hall 定理，左部大小为 $n$ ，然而右部大小仅为 $6$ ，所以枚举右部的子集即可。每个子集相邻的点数都大于等于左侧子集的大小 $n$ 。

8. P3980 [NOI2008] 志愿者招募

有 $n$ 天，每天至少需要 $a_i$ 个志愿者，有 $m$ 种志愿者，每种个数不限，价格为 $c_i$ ，负责 $[l_i,r_i]$ 的工作。求最少花费。

无论是单纯性还是上下界都比原做法好理解多了。

用上下界网络流，$i\to i+1$ 连下界为 $a_i$ 的边，$r_i\to l_i$ 连 $[0,\text{infin}]$ ，价格为 $c_i$ 的边，跑无源汇费用流即可。

10. P2050 [NOI2012] 美食节

$n$ 个厨师 $m$ 份菜，$i$ 做 $j$ 号菜的时间是 $T_{i,j}$ 。第 $i$ 个顾客选择了 $a_i$ 号菜品。最小化所有人的等待时间之和。$n,m\le 40$

第 $i$ 个厨师做的第倒数 $j$ 份菜品为 $k$ ，对答案的贡献是 $T_{i,k}\times j$ 。于是可以把每个厨师拆成所有时刻。跑费用流即可。

11.P3749 [六省联考 2017] 寿司餐厅

有 $n$ 份寿司，你可以选择若干个不交极长段 $[l,r]$，一次选择的价值是 $\sum _{l\le i\le j\le r}{d}_{i,j}$ 。同时，每个 $i$ 有一个种类 $a_i$ ，表示如果有 $a$ 个选择的是种类 $x$ ，就要付出 $-m{x}^2+cx,m\in \{0,1\}$ 的负贡献，其中 $m$ 是给定的。求最大价值。

发现如果选择 $d[i,j]$ ，则一定要选择 $d[i+1,j]$ 和 $d[i,j-1]$ 。$d[i][i]$ 的值又相当于 $d[i][i]-a[i]$ ，再解决种类的问题，$d[i][i]\to a[i]$ ，$a[i]=m\ast a[i]\ast a[i]$

据此转换为最大权闭合子图问题即可。

12. P2805 [NOI2009] 植物大战僵尸

平面直角坐标系上有 $n$ 个植物，击败有 $c_i$ 的价值（可能为负数），第 $i$ 个植物还有一个攻击到的点的集合 $S$ ，且伤害是秒杀。

你是僵王博士，僵尸从右侧进入，吃 $(i,j)$ 前必须吃 $(i,j+1)$ 。求最大可能的价值是多少。

两种保护关系形成一个有向图，$u\to v$ 表示吃 $u$ 前必须先吃 $v$ 。建图跑最大权闭合子图即可。

但是保护关系会 成环 ，而且任意能到达环上的点同时也不能选。用反图拓扑排序处理即可。

13. Pumping Stations

给定一个图，你需要构造一个排列，收益为 $\sum \text{mincut}(a_{i-1},a_i)$ ，使得收益最大。并求出方案。

最小割树模板题，考虑分治建出最小割树。最小割等于路径上最小值，则树上最小边是只经过一次的，再分治进行处理。

14. P4298 [CTSC2008] 祭祀

给定一个DAG，你需要选择若干个点，满足任意两个点不能互相到达。最多化点的个数。

求出点的个数，并输出方案。

实际就是求 最长反链 。$n\le 100$

**Dilworth **定理指出：最长反链=最小“链”划分，注意这里的“链”不同于最小路径覆盖问题，而是指可交链。

那这个问题与 2. P2764 最小路径覆盖问题 的区别在于：链可以被“挖空”，只保留端点。

因此我们用 Floyd传递闭包 建出每个点能够到达的点，再在这张新图上做原问题最大流即可解决第一问。

容易发现，因为无环，用传递闭包所建出的图是二分图。

第二问要输出一个可行的方案，实际就是 二分图最大独立集 ，按照其输出方案的套路做即可：

从左侧未匹配的点出发 dfs，从左往右只走非匹配边 ，从右往左只走匹配边，最小点覆盖即为 左侧的未访问点+右侧的访问点。最大独立集即为： 左侧的访问点+右侧的未访问点。

第三问求：是否存在一个最大方案选择了点 $i$ ，这个好办，只需要删掉点 $i$ 相连的，和连向点 $i$ 的所有点和边（也即默认 选了 $i$ ）。再跑最大匹配，看是否等于原答案减一即可。

因为传递闭包，$m=O(n^2)$，复杂度：$O(n^{3.5})$ 。

Part9. 其他习题

1. Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

建立起点 $s$ 和终点 $t$ ，$s$ 向每天连上界为 $d_i$ 的边，每天向每个人连 $[l_i,r_i]$ 的边，每个人向终点连下界为 $g_i$ 的边，转换成有源汇上下界最大流问题。注意虚拟源点汇点。

Debug

第一步 dinic() 得到的最大流应该是 e[tot].w ，而非 dinic() 。

模拟费用流

二分图

竞赛幽灵，难在一些套路化的建模上。

如果两个贡献独立————贡献在坐标上————转换成二分图 。

Part2. 二分图神仙建模

1.给定 $2n$ 个点，点有横纵坐标，我们称 一对点是好的，当且仅当横坐标相同或纵坐标相同。

最大化好的配对的数量，要求每个点都在一个配对中。

套路：横坐标连纵坐标。

2.给定一张 $n\ast m$ 网格图，有 $k\le {10}^6$ 个障碍。你一次可以跳到当前行或当前列任意一个没有障碍的点。求所有能跳到的点需要的跳跃次数的总和。 $n,m\le {10}^5$ 。

套路：每个障碍横坐标连纵坐标，转换成补图最短路。

给定一个 $n^2$ 矩阵，每个点有 $p_i$ 概率为 $1$ ，否则为 $0$ ，求矩阵积和式 $>0$ 的概率。$n\le 7$。

积和式即为不带系数的行列式：$\sum _p\prod a[i][p_i]$。

如果一个点是 $1$ ，相当于行列连边，问题转化为二分图完美匹配存在性。

Summary

在矩阵/网格图 上，多思考二分图 $i\to j$。贡献独立，也要想二分图。

Part3 二分图相关问题和定理

1. 最大匹配

若边集 $M$ 满足任意两条边不交于同一端点，则称为匹配。

特殊的，$|M|=|V_1|=|V_2|$ 被称为完美匹配。

$\text{König}$ 定理指出：二分图最大匹配在数值上等于最小点覆盖。

2. 最小点覆盖集

给定二分图 $G=\{V,E\}$ ，若一个点集 $C$ 满足 $\mathrm{\forall }(u,v)\in E$ ，有 $u\in C\text{or}v\in C$ 。通俗的说，一个点可以覆盖相邻的边，能覆盖所有边的点集就是点覆盖集。

构造方法：先求出一组最大匹配，从左侧未匹配的点出发 dfs，从左往右只走非匹配边 ，从右往左只走匹配边，最小点覆盖即为 左侧的未访问点+右侧的访问点。

3. 最大独立集

若点集 $I$ 满足 任意两点不直接相连 ，则称 $I$ 为独立集。

二分图最大独立集 $=V-$ 最小点覆盖集。

4. 最大团

若 点导出子图 $G^{\prime }=\{V^{\prime },E^{\prime }\}$ 满足 $\mathrm{\forall }u,v\in V^{\prime },u\in V_1,v\in V_2$ ，均有 $(u,v)\in E^{\prime }$ 。则称 $G^{\prime }$ 为 $G$ 的最大团。

二分图最大团等于 补图最大独立集 。

平面图

定义

如果图能画在平面上，边之间两两无交（边不能画曲线），则称其为平面图。

$K_5$ 和 $K_{3,3}$ 都不是平面图，其中 $K_5$ 指的是点数为 $5$ 的平面图，而 $K_{3,3}$ 指的是两边各有三个点的完全二分图。

判断：若两个图是同构的，或者两个图在不断增加或消去二度顶点后同构，则称两个图是同胚的。

库拉图斯基定理指出：图 $G$ 是平面图当且仅当不含有与 $K_5$ 和 $K_{3,3}$ 同胚的子图。

平面图转对偶图

通俗的讲，对偶图是在平面图上每个封闭图形中放一个节点，节点之间边的·边权即为原图与这条边相交的边权。

例如下图为狼抓兔子一题中的平面图转对偶图。

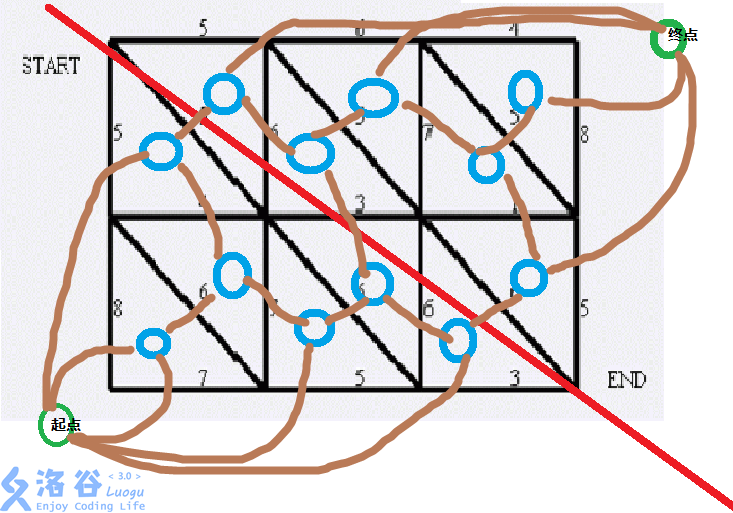
原题答案为 14，即为切断右下角的三条边：3 6（不清楚） 5。

可以发现，平面图的最小割即为对偶图的最短路。

P7916 [CSP-S 2021] 交通规划

给定一个 $n\ast m$ 的网格，但每一条边都是无限长的射线，格点间的小边有边权。$Q$ 次询问，额外给定 $k$ 个位于射线上的特殊点，并钦定了他们的颜色。你需要确定中间格点上的颜色，使得代价最小。代价计算的方式为：颜色不同的两个点之间的短边边权之和。颜色只有 0/1。

$n,m\le 500,\sum k\le 50$。

一半难度在读题和建对偶图（仅指代码实现）。

对于 $n\le 100$，就是裸的集合划分模型，相邻格点之间连双向边，与源点汇点连边权为 0 的边。钦定颜色的格点只能连源点/汇点。问题转换为（非平面图）求最小割。

考虑 $k=2$ 的做法，如果颜色相同，那么全部染为相同的颜色，代价为 $0$，否则，问题转换为狼追兔子。平面图最小割转换为对偶图最短路即可。

考虑从 $k=2$ 的做法启发正解，首先显然的是，相邻两个颜色相同的特殊点可以合并处理，因为他们中间一定不存在割。那这样特判掉只有一种颜色的特殊情节，外面的特殊点会围成一个长度为偶数，黑白颜色交替的环。

因为外面的点很少，只有 $k\le 50$，所以我们完全可以跑 $k$ 次最短路，求出从每个点出发跑对偶图得到的最小割，即对 $(\genfrac{}{}{0ex}{}{k}{2})$ 种不同情况做 $k=2$。

考虑最终的匹配结果，即割的形状，可以发现割一定不交，否则可以看做“碰头再返回”。因此最终的匹配是类括号序列的形式，区间 dp 即可求解。复杂度 $O(\sum k\times nm\log +\sum k^3)$。

太难写了！