[JLOI2015] 骗我呢——一类经典反射容斥

反射容斥

一层反射：有一条线 \(y=x+b\) 不能碰到。

从第一次碰到直线开始，将后面的部分沿直线翻折，最终一定会到达 \((n-b,n+b)\)，因为 \(b\ne 0\)，所以构成双射。答案即为 \(\binom{2n}{n}-\binom{2n}{n-b}\)。

注意，如果最终到达的位置是 \((n,m)\)，反射后 \(n,m\) 会互换，答案为 \(\binom{n+m}{m}-\binom{n+m}{n-1}\)。

卡特兰数

将左括号看作向右，右括号看作向上，则等价于不能碰到 \(y=x+1\)，故卡特兰数有组合意义：\(\binom{2n}{n}-\binom{2n}{n-1}\)。

二层反射容斥

每一次碰到线后记录 AAABBBAABBABA的形式，相邻的合并，得到ABABAB的形式，容斥即可，正确性地方太小。

设第一条线为 \(y_1=x+l,y_2=x+r\)，\(l<0<r\)，那么有答案：

\[ans=\sum_{k\in \Z}\binom{n+m}{n-k(r-l)}-\binom{n+m}{n-k(r-l)+r} \]

注意：\(k\in \Z\)，只需要求组合数有意义即算入答案。

P3266 [JLOI2015] 骗我呢

求有多少个 \(n\times m\) 的数组，满足 \(x_{i,j}<x_{i,j+1},x_{i,j}<x_{i-1,j+1}\)，每个位置可以填 \([0,m]\) 的数。

\(n,m\le 10^6\)。

容易观察到每一行都是递增的，而且每一行都恰好少一个数，且少的这个数是单调递增的，我们可以直接列 DP 方程。

设 \(dp_{i,j}\) 表示第 \(i\) 行少的数是 \(j\)，有：

\[dp_{i,j}=\sum_{k=1}^{k\le j+1}dp_{i-1,k}=dp_{i,j-1}+dp_{i-1,j+1} \]

是形式上非常简洁的 DP，系数均为 \(1\)，但不能进行任何数据结构优化。我们考虑放在网格图上计数

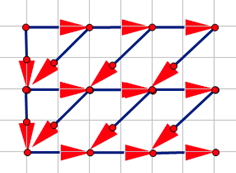
注意到只有第一列有直上直下的转移，这是因为 \(dp_{i,0}=1\)。

我们从第二行开始，每一行在上一行的基础上向右平移一格，就可以得到标准的转移：

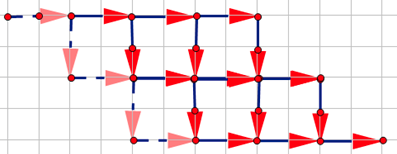
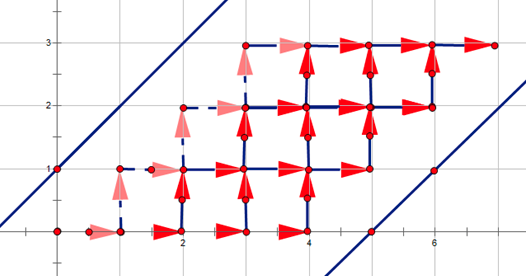
发现相当于不能碰直线 \(y_1=x+1\)，\(y_2=x-(m+2)\)。

#include <bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
int read(){
	char c=getchar();int h=0,tag=1;
	while(!isdigit(c)) tag=(c=='-'?-1:1),c=getchar();
	while(isdigit(c)) h=(h<<1)+(h<<3)+(c^48),c=getchar();
	return h*tag;
}
void fil(){
	freopen("data.in","r",stdin);
	freopen("data.out","w",stdout);
}
const int mod=1e9+7;
const int N=3e6+5;
int fac[N],inv[N];
int ksm(int a,int b) {
	if(b==1) return a%mod;
	int s=ksm(a,b/2);s=s*s%mod;
	if(b%2==1) s=s*a%mod;
	return s%mod;
}
int binom(int n,int m) {
	if(m<0||n<m) return 0;
	return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main(){
//	fil();
	int n=read(),m=read();
	int l=-m-2,r=1;
	int _n=n+m+1,_m=n;
	inv[0]=1,fac[0]=1;
	for(int i=1;i<=N-100;i++) fac[i]=fac[i-1]*i%mod,inv[i]=ksm(fac[i],mod-2)%mod;	
	int ans=0;
	for(int i=-1000000;i<=N;i++) {
		if(_n-i*(r-l)+r>(_n+_m)) continue;
		if(_n-i*(r-l)<0) break;
		ans+=binom(_n+_m,_n-i*(r-l))-binom(_n+_m,_n-i*(r-l)+r);
		ans=(ans+mod)%mod;
	}
	cout<<ans<<endl;
	
	return 0;
}