P6348

P6348 [PA2011]Journeys

有 $n$ 个点，$m$ 次连边，每次在两区间 $[a,b],[c,d]$ 的每两个点之间连一条无向边。
求问点 $p$ 到达其余的每个点所需经过的最少路径数。

$1\le n\le 5\times 10^5,1\le m\le 10^5,1\le a\le b\le n,1\le c\le d\le n$。

线段树优化建图，区间之间连边的模板题。

很明显直接暴力连边的时间和空间复杂度都是 $O(m\,n^2)$，所以要用到线段树优化建图来优化建边的复杂度。
我们可以利用“对于每一个区间，都可以将其转化为线段树上至多 $\log_2n$ 个区间”这一性质，来减少连边的数量。
先建出线段树，连边时改为向线段树上的表示相应的区间的节点连边。
线段树上的父子节点之间连边权为 0 的有向边，根据题目连边要求确定方向，此题要建两棵线段树。

• 如果是点向区间连边，就将点连向树中父节点向子节点连边的线段树中节点。
• 如果是区间向点连边，就从树中子节点向父节点连边的线段树上的相应节点向要求的节点连边。

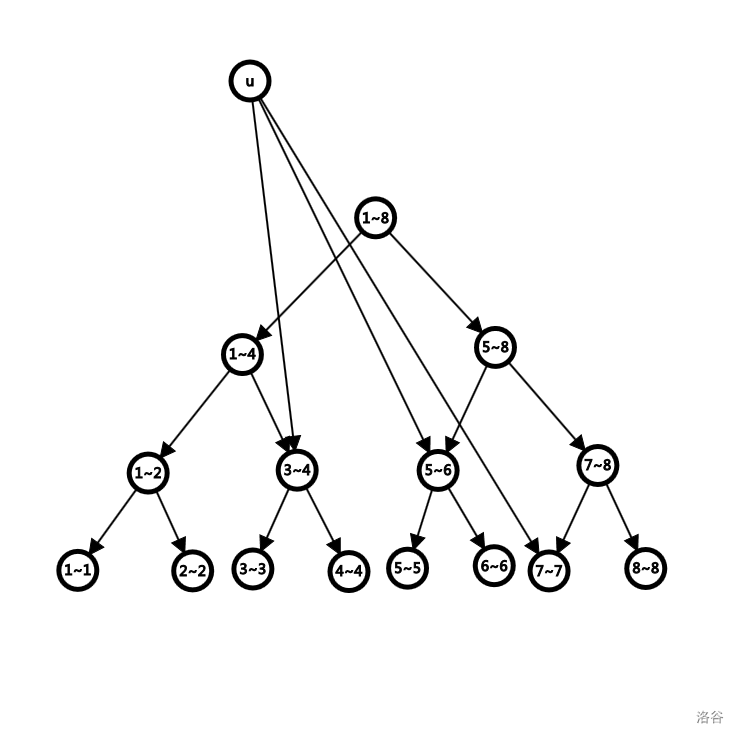
比如图中的例子就是点 u 向区间 $[3,7]$ 之间的点连边时的情况。

建出两棵线段树，其中一棵的每个父节点向其子节点连边权为 0 的单向边，另一棵则与之相反。
对于每次区间连边操作，在两棵线段树上找出对应节点并暴力连边，空间复杂度为 $O(n \log_2^2n)$，仍需优化。

考虑每次建边时引入一个虚点，在虚点和两棵线段树之间分别连两条方向相反的权值为 1 的有向边，空间复杂度降到 $O(n\log_2n)$，可以通过。

不直接直接只连一条无向边的原因是，如果两条连接虚点和线段树上节点的无向边经过了同一个点，则会让这个线段树上的节点可以通过线段树上的路径到达每一个节点。

建完边后以 $p$ 为起点跑一遍 01BFS 即可。
最后距离应除二，因为一条边被拆成了连向虚点从虚点连向目标点两个部分，边权算了两次。

#include <bits/stdc++.h>
#define MID int m=(l+r)>>1;
using namespace std;
const int N = 8e6;
int rd() {
    int w = 0, v = 1;
    char c = getchar();

    while (c < '0' || c > '9') {
        if (c == '-')
            v = -1;

        c = getchar();
    }

    while (c >= '0' && c <= '9')
        w = (w << 1) + (w << 3) + (c & 15), c = getchar();

    return w * v;
}
void wr(int x) {
    if (x < 0)
        putchar('-'), x = -x;

    if (x > 9)
        wr(x / 10);

    putchar(x % 10 + '0');
}
int fir[N], c, cnt, ls[N], rs[N], n, m, p, r1, r2, xd, vis[N], d[N];
deque <int>q;
struct E {
    int v, nt, w;
} e[N];
void I(int u, int v, int w = 0) {
    e[++cnt] = (E) {
        v, fir[u], w
    };
    fir[u] = cnt;
}
void b1(int &p, int l, int r) {
    if (l == r) {
        p = l;
        return;
    }

    p = ++c;
    MID b1(ls[p], l, m);
    b1(rs[p], m + 1, r);
    I(p, ls[p]);
    I(p, rs[p]);
}
void b2(int &p, int l, int r) {
    if (l == r) {
        p = l;
        return;
    }

    p = ++c;
    MID b2(ls[p], l, m);
    b2(rs[p], m + 1, r);
    I(ls[p], p);
    I(rs[p], p);
}
void ch(int p, int l, int r, int L, int R, bool f) {
    if (l >= L && r <= R) {
        if (f)
            I(p, xd, 1);
        else
            I(xd, p, 1);

        return ;
    }

    MID if (L <= m)
        ch(ls[p], l, m, L, R, f);

    if (R > m)
        ch(rs[p], m + 1, r, L, R, f);

    return ;
}
void dj(int p) {
    memset(d, 0x7f, sizeof(d));
    d[p] = 0;
    q.push_front(p);

    while (!q.empty()) {
        int u = q.front(), v, w;
        q.pop_front();

        for (int i = fir[u]; i; i = e[i].nt) {
            v = e[i].v, w = e[i].w;

            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;

                if (w == 1)
                    q.push_back(v);
                else
                    q.push_front(v);
            }
        }
    }
}
signed main() {
    n = rd(), m = rd(), p = rd();
    c = n;
    b1(r1, 1, n), b2(r2, 1, n);
    xd = c + 1;

    for (int i = 1, a, b, c, d; i <= m; i++)
        a = rd(), b = rd(), c = rd(), d = rd(), ch(r2, 1, n, a, b, 1), ch(r1, 1, n, c, d, 0), xd++, ch(r2, 1, n, c, d,
                                          1), ch(r1, 1, n, a, b, 0), xd++;

    dj(p);

    for (int i = 1; i <= n; i++)
        wr(d[i] / 2), putchar('\n');

    return 0;
}