网络最大流(序)
网络最大流
前言
网络流是一种神奇的问题,在不同的题中你会发现各种各样的神仙操作。
而且从理论上讲,网络流可以处理所有二分图问题。
二分图和网络流的难度都在于问题建模,一般不会特意去卡算法效率,所以只需要背一两个简单算法的模板就能应付大部分题目了。
单纯只是为了A掉P3376 【模板】网络最大流,并且尽量效率高,把最最最板子的网络流整一遍。
概念
- 网络流:一种类比水流的解决问题的方法。
- 网络:可以理解为有一个源点和汇点的有向图。
- 弧:也就是图中的有向边。
- 弧的流量:简称流量,网络中的每条边都有一个流量,表示为 \(f(x,y)\),可以为负数。
- 弧的容量:简称容量,网络中的每条边都有一个容量,表示为 \(c(x,y)\)。
- 源点:类比起点,能无限放出流量,表示为 \(S\)。
- 汇点:类比终点,能无限接受流量,表示为 \(T\)。
- 容量网络: 拥有源点和汇点且每条边都给出了容量的网络。
- 流量网络: 拥有源点和汇点且每条边都给出了流量的网络。
- 弧的残余容量:简称残余容量。在残量网络中每条边都会有一个残余容量。
对于每条边,残余容量 = 这条边的容量 - 这条边的流量。 - 残量网络:拥有源点和汇点且每条边都有残留容量的网络。残量网络 = 容量网络 − 流量网络。
初始残量网络就是容量网络。
可以参照下图理解。
其中 \(c\) 表示容量,\(f\) 表示流量,\(flow\) 表示残余容量。
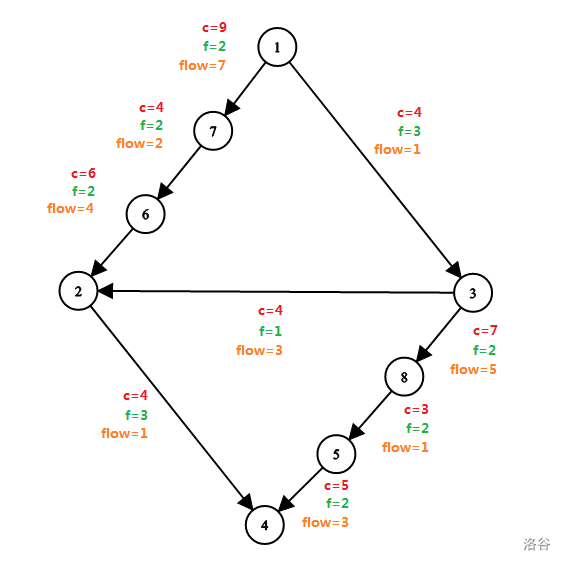
性质
- 容量限制:\(\forall(x,y)\in E,f(x,y)\le c(x,y)\)。(很明显流量不能大于容量)
- 流量守恒:\(\forall x\in V\) 且 \(x\ne S,x\ne T\),\(\sum_{(u,x)\in E}f(u,x) = \sum_{(x,v)\in E}f(x,v)\)。(很明显流进来多少就要流出去多少)
- 斜对称性:\(\forall (x,y) \in E,f(y,x)=-f(x,y)\)。
EK
概念
- 增广路:一条从残量网络中从 \(S\) 到 \(T\) 的路径,路径上所有边的残余流量都为正。
- 增广路定理:流量网络达到最大流当且仅当残量网络中没有增广路。
- 增广路算法:基于增广路的一种算法,核心为 bfs 找最短的增广路,并按照一般增广方法处理。
算法流程
- 用 bfs 找到任意一条经过边数最少的最短增广路,并记录路径上各边残留容量的最小值,因为木桶定律,容量最小的边不爆就行了。
- 根据残余流量最小值更新路径上边及其反向边的残留容量值。最大流加上其值。
- 重复流程 \(1,2\),直至无法找出增广路,结束算法。
算法解析
在实现算法的过程中,因为在残量网络跑增广路,所以只需记录最小的残余容量即可。
为了保证流量最大,所以要用到反悔的操作,在存图时建一条反向边权为零的边。
- 如果用邻接表或链式前向星存边,表示边的编号的变量要初始化为 \(1\),因为这样做对于某条边 \(i\),其反边就是 \(i \operatorname{xor} 1\)。(链表的性质)
- 如果用的是 vector 存边就只能记录反向边编号了。
当边 \((x,y)\) 的残余容量被用去了 \(f\) 时,其流量增加了 \(f\),残余流量应减少 \(f\),根据斜对称性,其反边 \((y,x)\) 的流量增加 \(-f\),残余流量增加 \(f\)。
那么如果在以后找增广路时选择了这一条边,就等价于:将之前流出去的流量的一部分(或者全部)反悔掉了个头,跟随着新的路径流向了其它地方,而新的路径上在到达这条边之前所积蓄的流量 以及 之前掉头掉剩下的流量 则顺着之前的路径流了下去。
同理,当使用了反向边 \((y,x)\) 的残留容量时也应是一样的操作。
图解
两次分别跑出一条增广路,用色笔画出。
图中只标出残余容量。
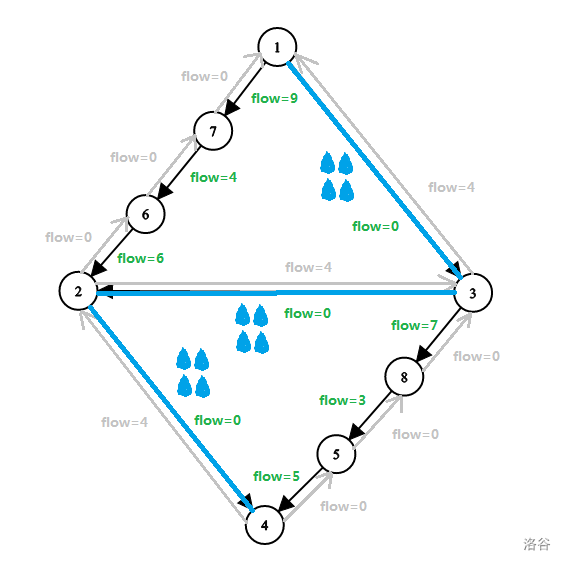
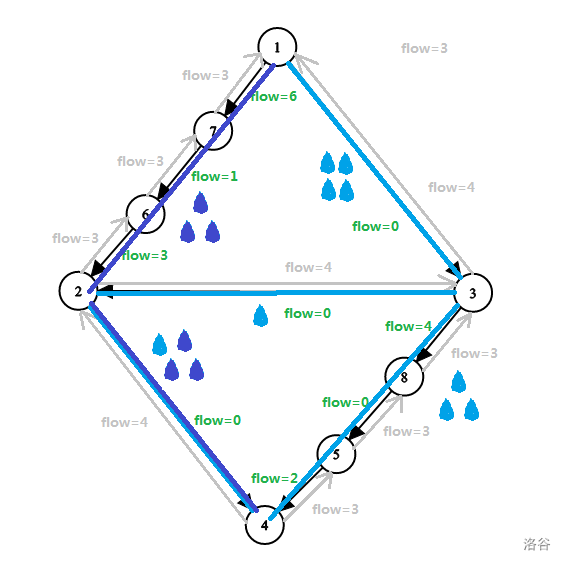
时间复杂度
\(O(nm^2)\)
因为使用 bfs 找到的必然是当前含边数最少的一条增广路,找一次需要 \(O(m)\) 的时间。
假如要利用反向边的话,必须走到一条边的尽头再往回走,这样一定比当前的最短路要大,所以是不会产生的,这样子我们就不用考虑容量改变的反向边。
每条增广路都有一个瓶颈,而两次增广的瓶颈不可能相同,所以增广路最多 \(m\) 条。
而增广路的长度是 \(\left[ 1,n \right]\),这就证明了 EK 的复杂度是 \(O(nm^2)\)。
实际一般跑的挺快,一般能解决 \(\left[ 10^3,10^4 \right]\) 规模的网络。
代码
#include <bits/stdc++.h>
using namespace std;
int rd() {
int w = 0, v = 1;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-')
v = -1;
c = getchar();
}
while (c >= '0' && c <= '9')
w = (w << 1) + (w << 3) + (c & 15), c = getchar();
return w * v;
}
const int N = 2e4, INF = 2e9;
int fir[N], c = 1, n, m, st, ed, f[N], p[N], mi[N];
long long ans;
queue <int>q;
struct E {
int v, nt, w;
} e[N];
void I(int u, int v, int w = 0) {
e[++c].v = v;
e[c].w = w;
e[c].nt = fir[u];
fir[u] = c;
}
bool bfs() {
for (int i = 1; i <= n; i++)
f[i] = 0;
q.push(st), f[st] = 1;
mi[st] = INF;
while (!q.empty()) {
int u = q.front(), V;
q.pop();
for (int i = fir[u]; i; i = e[i].nt)
if (e[i].w && !f[V = e[i].v])
mi[V] = min(mi[u], e[i].w), q.push(V), f[V] = 1, p[V] = i;
}
return f[ed];
}
void ek() {
while (bfs()) {
int x = ed;
ans += mi[ed];
while (x != st) {
int i = p[x];
e[i].w -= mi[ed];
e[i ^ 1].w += mi[ed];
x = e[i ^ 1].v;
}
}
cout << ans;
}
int main() {
n = rd(), m = rd(), st = rd(), ed = rd();
for (int i = 1, u, v, w; i <= m; i++)
u = rd(), v = rd(), w = rd(), I(u, v, w), I(v, u);
ek();
}
Dinic
更快的网络流算法,同时也是应用非常广泛的网络流算法,一般情况下不会被卡。
时间复杂度
相比于 EK 的 \(O(nm^2)\),Dinic 的 \(O(n^2m)\) 在稠密图上优势很大。
用于二分图匹配时,复杂度为 \(O(m\sqrt n )\)。
算法讲解
首先,EK 跑得慢原因很容易想到,一次 bfs 可能要遍历整张图,却只能找到一条增广路。
而 Dinic 解决方法就是多路增广。
具体实现方法是两步:
- 跑 bfs 对网络分层。
- 用 dfs 跑增广路。
用下面的图作为例子。
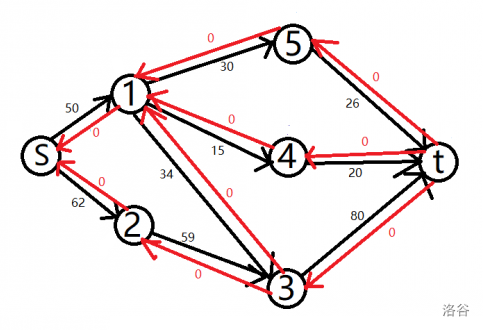
在跑 bfs 时,相比于 EK,不记录路径,只对所有点分层。
具体操作看 bfs 部分代码:
bool bfs(){
for(int i=1;i<=n;i++)d[i]=0;
q.push(st);d[st]=1;
while(!q.empty()){
int u=q.front(),V;q.pop();
for(int i=fir[u];i;i=e[i].nt)
if(e[i].w&&!d[V=e[i].v])
d[V]=d[u]+1,q.push(V);
}return d[ed];
}
分层后的状况:
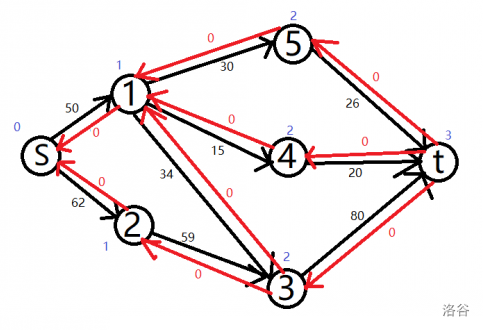
蓝色数字是点的层数。
分层是为了保证找到的路径是在最短增短路上。
比如下面的图(括号内的数是层数)
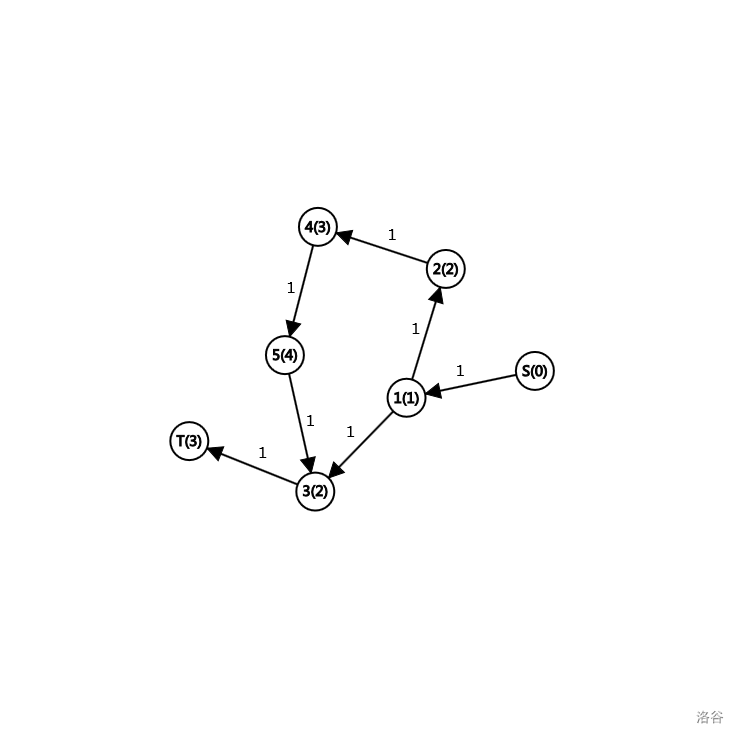
分层之后就不会走那条长路了。
bfs 分层之后的下一步是 dfs 增广。
还是用之前那张图作为例子:

分层之后 dfs 跑增广路。
比如,第一条增广路跑 \(S \Longrightarrow 1 \Longrightarrow 4 \Longrightarrow T\)。
相应的流量发生变化,在图中已经标出。
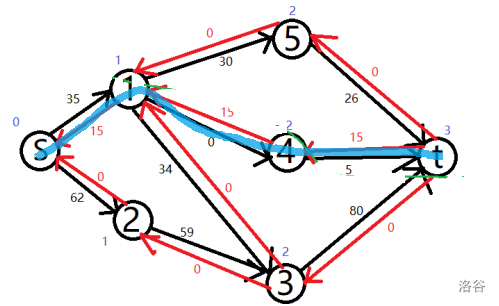
很明显,图中还有增广路,所以可以继续使用第一次 bfs 的标号跑增广路。
第二条增广路是 \(S \Longrightarrow 1 \Longrightarrow 5 \Longrightarrow T\),如图:
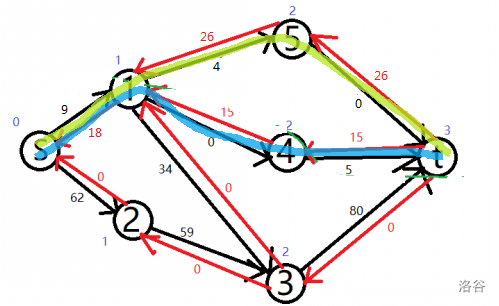
还有第三条增广路:\(S \Longrightarrow 1 \Longrightarrow 3 \Longrightarrow T\)。
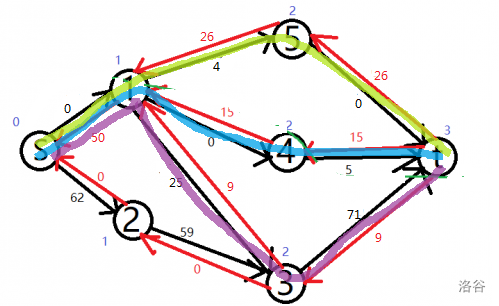
最后是第四条增广路: \(S\Longrightarrow 2\Longrightarrow 3 \Longrightarrow T\)
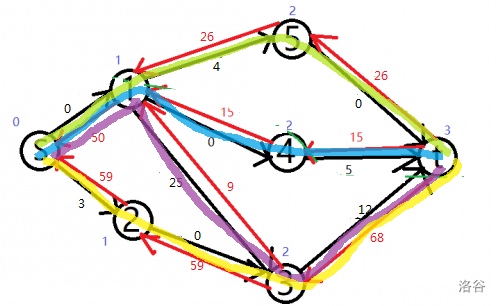
综上,一次 dfs 能找到多条增广路,这就是 dinic 的高效原因。
然后就可以把 dinic 的代码写出来了。
#include <bits/stdc++.h>
using namespace std;
int rd() {
int v = 1, w = 0;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-')
v = -1;
c = getchar();
}
while (c >= '0' && c <= '9')
w = (w << 1) + (w << 3) + (c & 15), c = getchar();
return w * v;
}
const int N = 2e4, INF = 2e9;
int c = 1, fir[N], n, m, st, ed, d[N];
queue <int>q;
long long ans;
struct E {
int v, nt, w;
} e[N];
void I(int u, int v, int w = 0) {
e[++c].v = v;
e[c].w = w;
e[c].nt = fir[u];
fir[u] = c;
}
bool bfs() {
for (int i = 1; i <= n; i++)
d[i] = 0;
d[st] = 1;
q.push(st);
while (q.size()) {
int u = q.front(), V;
q.pop();
for (int i = fir[u]; i; i = e[i].nt)
if (!d[V = e[i].v] && e[i].w)
q.push(V), d[V] = d[u] + 1;
}
return d[ed];
}
int dfs(int u, int fl) {
if (u == ed)
return fl;
int V, tmp = 0;
for (int i = fir[u]; i; i = e[i].nt)
if (e[i].w && d[V = e[i].v] == d[u] + 1 && (tmp = dfs(V, min(fl, e[i].w)))) {
e[i].w -= tmp, e[i ^ 1].w += tmp;
return tmp;
}
return 0;
}
void dinic() {
int g;
while (bfs()) {
while (g = dfs(st, INF))
ans += g;
}
cout << ans << endl;
return ;
}
int main() {
n = rd(), m = rd(), st = rd(), ed = rd();
for (int i = 1, u, v, w; i <= m; i++)
u = rd(), v = rd(), w = rd(), I(u, v, w), I(v, u);
dinic();
return 0;
}
Loj 的提交记录
洛谷的提交记录
都收获了 TLE。
因为单路增广的 dinic 的时间复杂度是不能保证的,所以要对此进行优化。
多路增广
一次 bfs 会找到 \(\left[ 1,m \right]\) 条增广路,大大减少了 bfs 次数,但 dfs 更新路径上的信息仍是在单路增广,效率相较于 EK 并没有多大变化。
用一个变量存经过路径上的最小流量,在 dfs 找到一条增广路之后不直接返回,回溯更新之前的信息,直至流量达到上限。
代码只放了有改变的部分。
int dfs(int u, int fl) {
int V, f;
if (u == ed)
return fl;
for (int i = fir[u]; i; i = e[i].nt)
if (e[i].w && d[V = e[i].v] == d[u] + 1 && (f = dfs(V, min(fl, e[i].w)))) {
e[i].w -= f;
e[i ^ 1].w += f;
return f;
}
return 0;
}
void dinic() {
while (bfs())
ans += dfs(st, INF);
//因为可以多路同时增广,所以每个分层图只要跑一次 dfs 即可
cout << ans << endl;
return ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号