线段树优化建图学习笔记

线段树优化建图

起因

一般情况下，连边发生在两个点之间。
但在某些题目中，要在点和区间之间连边。
所以有了线段树优化建图。

原理

从模板题看起。
显然，直接暴力连边的最坏时间复杂度和空间复杂度都为 \(O(n^2)\)。
线段树建图的原理就是建出线段树，区间连边转化为向线段树上的节点连边。

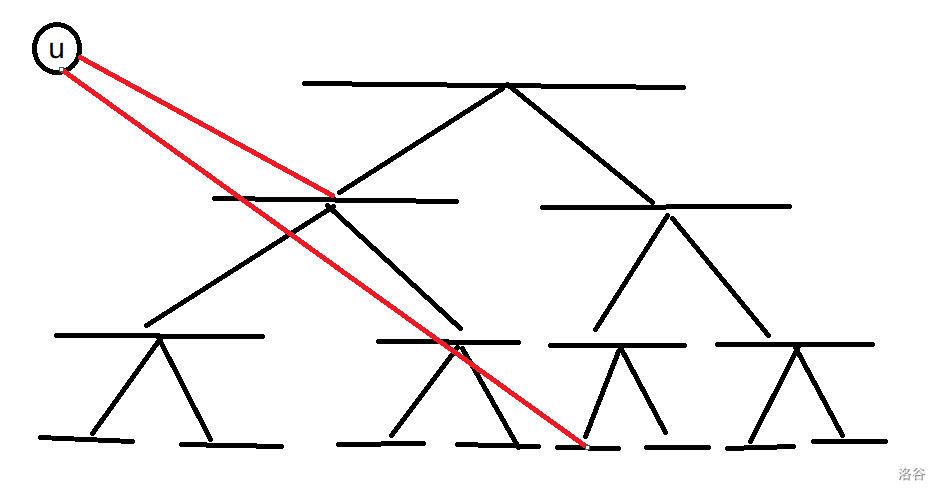
但只是如图所示的连边是不够的，对于区间中的所有点都要连边。
所以父子节点之间连边权为 \(0\) 的边就能解决问题了。
至于连边的方向由要求决定。

• 如果要求点向区间连边，线段树上就从父节点向子节点连边，目标点向线段树上节点连边。
• 如果要求区间向点连边，线段树上就从子节点向父节点连边，线段树上节点向目标点连边。

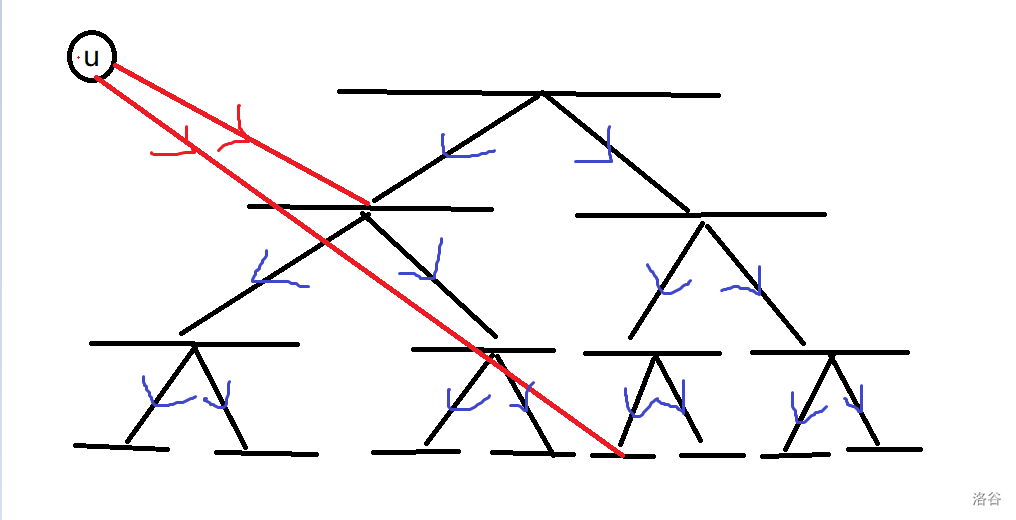
还有一个小细节点：编号问题。
如果直接按照朴素方法建出线段树，则树上节点的编号可能会与题目中的节点编号产生冲突。
解决方法是，利用类似于动态开点线段树的写法，每个线段树节点从 \(n\) 开始分配，其中叶子节点的编号就是区间本身，也就省去了某些写法要在两棵线段树的叶子节点之间连边的操作。
建树的代码：

void b1(int &p,int l,int r){if(l==r){p=l;return ;}p=++tot;MID b1(ls[p],l,m);b1(rs[p],m+1,r);I(p,ls[p]),I(p,rs[p]);}
void b2(int &p,int l,int r){if(l==r){p=l;return ;}p=++tot;MID b2(ls[p],l,m);b2(rs[p],m+1,r);I(ls[p],p),I(rs[p],p);}

看回到题目，题目要求点之间连边，点向区间连边，区间向点连边，求最短路。
建出两棵线段树，然后按要求连边即可。

#include <bits/stdc++.h>
#define MID int m=(l+r)>>1;
using namespace std;const int N=8e6;int rd(){
	int w=0,v=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')v=-1;c=getchar();}
	while(c>='0'&&c<='9')w=(w<<1)+(w<<3)+(c&15),c=getchar();return w*v;
}void wr(int x){if(x<0)putchar('-'),x=-x;if(x>9)wr(x/10);putchar(x%10+'0');}
int fir[N],c,cnt,ls[N],rs[N],n,m,p,r1,r2,xd,vis[N],d[N];deque <int>q;struct E{int v,nt,w;}e[N];
void I(int u,int v,int w=0){e[++cnt]=(E){v,fir[u],w};fir[u]=cnt;}
void b1(int &p,int l,int r){if(l==r){p=l;return;}p=++c;MID b1(ls[p],l,m);b1(rs[p],m+1,r);I(p,ls[p]);I(p,rs[p]);}
void b2(int &p,int l,int r){if(l==r){p=l;return;}p=++c;MID b2(ls[p],l,m);b2(rs[p],m+1,r);I(ls[p],p);I(rs[p],p);}
void ch(int p,int l,int r,int L,int R,bool f){
	if(l>=L&&r<=R){if(f)I(p,xd,1);else I(xd,p,1);return ;}
	MID if(L<=m)ch(ls[p],l,m,L,R,f);if(R>m)ch(rs[p],m+1,r,L,R,f);return ;
}void dj(int p){
	memset(d,0x7f,sizeof(d));d[p]=0;q.push_front(p);while(!q.empty()){
		int u=q.front(),v,w;q.pop_front();
		for(int i=fir[u];i;i=e[i].nt){
			v=e[i].v,w=e[i].w;if(d[v]>d[u]+w){d[v]=d[u]+w;if(w==1)q.push_back(v);else q.push_front(v);}
		}
	}
}signed main(){
	n=rd(),m=rd(),p=rd();c=n;b1(r1,1,n),b2(r2,1,n);xd=c+1;for(int i=1,a,b,c,d;i<=m;i++)
	a=rd(),b=rd(),c=rd(),d=rd(),ch(r2,1,n,a,b,1),ch(r1,1,n,c,d,0),xd++,ch(r2,1,n,c,d,1),ch(r1,1,n,a,b,0),xd++;dj(p);
	for(int i=1;i<=n;i++)wr(d[i]/2),putchar('\n');return 0;
}

应用