主席树学习笔记
主席树
主席树是由一位巨佬 hjt 发明的,所以叫主席树。
什么是主席树
主席树,又名可持久化权值线段树。所以,主席树 \(\in\) 可持久化线段树
至于可持久化的定义,简单来说就是可以访问到之前某个时刻的数据。
比如\(\color{Blue}{模板题1}\)中的要求:求单点历史值,修改某历史版本的单点值。
如何做到可持久化
原理
有一个很朴素的想法:对于每种历史版本,都开一棵线段树维护,查询和修改就在要求的历史版本所对应的线段树上进行。
但是很明显这样会 MLE,因为空间复杂度达到了 \(O(4 \cdot n \cdot m)\)。
优化
实际上的主席树长这样: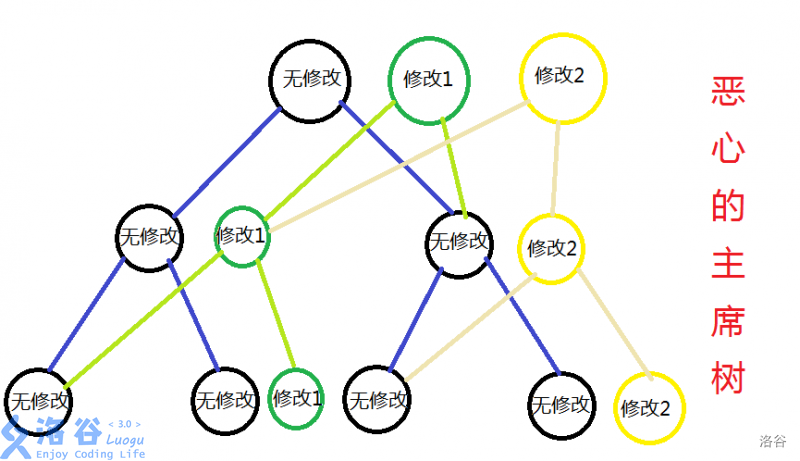
因为很容易发现,在每次进行更新的操作时,发生改变的节点并不是整棵线段树上的所有节点。
以下面的权值线段树为例:
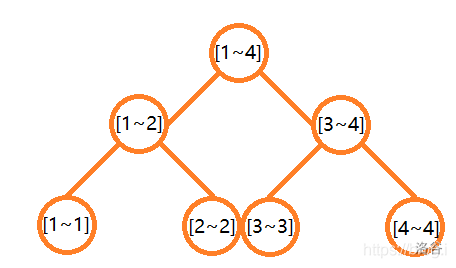
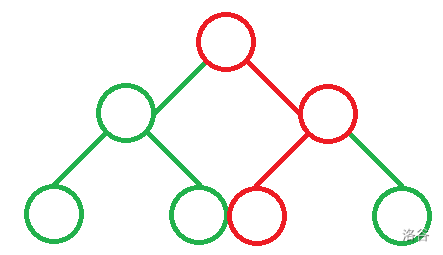
如果在权值线段树上加入 3,发生改变的节点只有图中标红的节点。
结合权值线段树的性质可知,每次单点修改,被改变的节点数是 \(O(\log_2n)\)
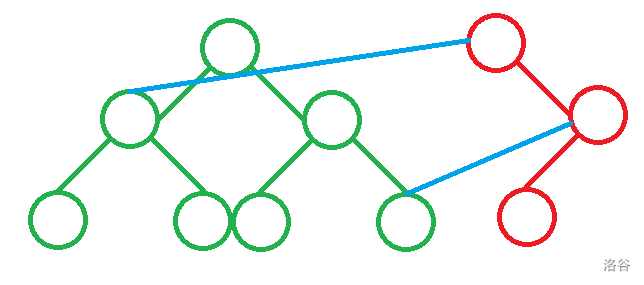
所以完全可以只复制发生改变的节点,并与没有改变的节点相连。
从而做到利用原先线段树中未被修改的节点,大量节省空间。
模板题1
\(\color{Blue}{Luogu P3919 【模板】可持久化线段树 1(可持久化数组)}\)
维护一个长为 \(n\) 的数组,支持两种操作。
- 将历史版本为 \(v_i\) 的数组中位置为 \(loc_i\) 的元素的值修改为 \(value_i\)。
- 求历史版本为 \(v_i\) 的数组中位置为 \(loc_i\) 的元素的值,即 \(a_{loc_i}\)。
每次操作后生成一个新的样本,编号为当前操作数编号 \(i\)。
思路
很明显要用主席树维护,但是主席树和一般的线段树还是有差别的。
Q:如何创造新节点?新节点如何编号?新节点如何连边?
A: 创造新节点直接开内存池就行,编号就是此时总节点数 \(+1\),至于连边,开结构体用指针解决。
Q: 如何访问子节点?
A: 和动态开点线段树相似,不是普通线段树那样 \(*2||*2+1\),而是结构体中存储节点的左右儿子。
Q: 怎样存根?
A:单独开一个数组。
代码实现
在开始之前,先用一些宏定义减少代码量。
#define MID int m=(l+r)>>1;
#define L s[p].l,l,m
#define R s[p].r,m+1,r
首先要定义线段树的结构体变量,共有三个值:左儿子,右儿子,权值。
struct tree{int l,r,val;}s[N<<3];
新建节点的操作:
int add(int p){s[++top]=s[p];return top;}
//新节点的编号是节点数+1,节点内容与原节点信息相同
建树:
void build(int &p,int l,int r){
p=++top;if(l==r){s[p].val=a[l];return ;}MID
build(L);build(R);return ;
}//其实建树的差别只是在新建节点上
单点修改:
int change(int p,int l,int r,int x,int val){
p=add(p);if(l==r)s[p].val=val;
else{MID if(x<=m)s[p].l=change(L,x,val);else s[p].r=change(R,x,val);}return p;
}//更新操作和普通权值线段树相似,只是要新建节点
单点查询:
int query(int p,int l,int r,int x){
if(l==r)return s[p].val;MID
if(x<=m)return query(L,x);else return query(R,x);
}
最后是完整的代码:
#include <bits/stdc++.h>
#define MID int m=(l+r)>>1;
#define L s[p].l,l,m
#define R s[p].r,m+1,r
using namespace std;int rd(){
int w=0,v=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')v=-1;c=getchar();}
while(c>='0'&&c<='9'){w=(w<<1)+(w<<3)+(c&15);c=getchar();}return w*v;
}void wr(int x){
char c[20];int l=0;if(x<0){putchar((1<<5)+(1<<3)+(1<<2)+1);x=~x+1;}
do{c[l++]=x%10+(1<<4)+(1<<5);x/=10;}while(x>0);for(int i=l-1;i>=0;i--)putchar(c[i]);
}const int N=3e6;int n,top,q,a[N],rt[N<<3],r,o,x,y;
struct tree{int l,r,val;}s[N<<3];int add(int p){s[++top]=s[p];return top;}
void build(int &p,int l,int r){
p=++top;if(l==r){s[p].val=a[l];return ;}MID
build(L);build(R);return ;
}int change(int p,int l,int r,int x,int val){
p=add(p);if(l==r)s[p].val=val;
else{MID if(x<=m)s[p].l=change(L,x,val);else s[p].r=change(R,x,val);}return p;
}int query(int p,int l,int r,int x){
if(l==r)return s[p].val;MID
if(x<=m)return query(L,x);else return query(R,x);
}int main(){
n=rd(),q=rd();for(int i=1;i<=n;i++)a[i]=rd();build(rt[0],1,n);
for(int i=1;i<=q;i++){
r=rd(),o=rd(),x=rd();
if(o==1){y=rd();rt[i]=change(rt[r],1,n,x,y);rt[i]=rt[r];}
else{wr(query(rt[r],1,n,x));putchar('\n');rt[i]=rt[r];}
}return 0;
}
模板题2
其实这个模板题才是最一开始主席树发明时用来解决的问题:区间静态第 \(k\) 小。
\(\color{Blue}{Luogu P3834 【模板】可持久化线段树 2}\)
给定长度为 \(n\) 的序列 \(a\),对于每次询问输出闭区间 \(\left[ l,r \right]\) 之内的第 \(k\) 小值。
解决思路
肯定是用主席树(废话)。
而且这次用的是静态主席树。
对于原序列的每个前缀 \(\left[ 1 \dots i \right]\) 建立一棵线段树维护其值域上每个数出现的次数,则其线段树是可加减的。 ————发明者原话
可以加减的原因:因为主席树的每个节点都维护一棵线段树, 维护的区间信息和结构相同,因此具有可加减性。
先对给出的序列 \(a\) 离散化。\(\color{Maroon}{离散化笔记}\)。
离散化后的 \(b\) 数组中,存储 \(a\) 中每个数排序并去重后的数,即 \(b_i \in \left[ 1,t \right]\)(\(t\) 是离散化去重后数字个数)。
线段树维护的就是区间 \(a_1 \dots a_i\) 中的数在数组 \(b\) 中出现次数。
以下举一个 \(\color{Blue}{Lpy-Now 的题解}\)中的例子。
举例
(例子中的操作似乎没有经过彻底的离散化,只是进行了排序和去重,不过应该理解起来问题不大)
假设给出的数组 \(a\) 为: $$4,1,1,2,8,9,4,4,3$$
那么处理后的数组 \(b\) 为: $$1,2,3,4,8,9$$
对数组 \(a\) 的前缀 \(a_{1 \dots 9}\) 建出权值线段树,每个数出现次数就是线段树节点的值。
线段树中的每个节点维护区间 \(\left[ i,j \right]\) 中出现了多少个 \(a_{1 \dots 9}\) 中的数字。
初始的线段树如下:

先从简单方面入手:对于整个区间的第 \(k\) 小值应如何求出?
比如,求区间 \(a_{1 \dots 9}\) 第 \(6\) 大值。
这样就和普通的权值线段树相同,这里只是简述一下。
- 从根节点开始,左儿子只有 \(4\) 个元素,说明第 \(6\) 大的值一定在右子树中。
- 根节点右儿子的左儿子中有 \(4\) 个元素,\(4+4=8>6\),说明第 \(6\) 大的值在左子树中。
- 重复以上的递归,一直到线段树叶子节点,当前叶子节点所代表的权值就是区间第 \(k\) 小值。
如果将其拓展到求区间 \(\left[ L,R \right]\) 的第 \(k\) 小值,如何去求?
因为对于数组 \(a\) 任意的 \(i\),都有 \(a_{1 \dots i}\) 的权值线段树,因为之前证明过其具有可减性,所以类似于前缀和的思想,对于 \(\left[ L,R \right]\) 的部分,只要在递归的过程中减去 \(\left[ 1,L-1 \right]\) 的部分即可。
因为对于每个前缀都建一棵线段树的空间消耗极大,所以要用到主席树。
注意点
- 建树时首先要建一棵空树,也就是最原始的主席树,再依次对其进行更新。
- 主席树是一种特殊的线段树,具有单次查询操作 \(O(\log_2n)\) 的时间复杂度,而且能访问历史版本。所以总时间复杂度为 \(O(n\log_2n)\),空间复杂度为 \(O(n\log_2n+n\log_2n)\)(前一个 \(O(n\log_2n)\) 是建空树的空间复杂度,后一个是存 \(n\) 种历史版本的空间复杂度)。
- 主席树对于空间的需求大,有时要用动态开点或离散化减少空间损耗。(好像空间回收也行,但不确定,因为还不会)。
完整代码
#include <bits/stdc++.h>
#define MID int m=(l+r)>>1;
#define L s[p].l,l,m
#define R s[p].r,m+1,r
using namespace std;int rd(){
int w=0,v=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')v=-1;c=getchar();}
while(c>='0'&&c<='9'){w=(w<<1)+(w<<3)+(c&15);c=getchar();}return w*v;
}void wr(int x){
char c[20];int l=0;if(x<0){putchar((1<<5)+(1<<3)+(1<<2)+1);x=~x+1;}
do{c[l++]=x%10+(1<<4)+(1<<5);x/=10;}while(x>0);for(int i=l-1;i>=0;i--)putchar(c[i]);
}const int N=2e5+1e2;int n,q,a[N],b[N],cnt,rt[N],t;
struct tree{int l,r,v;}s[N*20];void add(int &p){s[++t]=s[p];p=t;}
void c(int &p,int l,int r,int x){add(p);s[p].v++;if(l==r)return ;MID if(x<=m)c(L,x);else c(R,x);}
int query(int l,int r,int k,int ll,int rr){
if(l==r)return l;MID int val=s[s[rr].l].v-s[s[ll].l].v;
if(k<=val)return query(l,m,k,s[ll].l,s[rr].l);else return query(m+1,r,k-val,s[ll].r,s[rr].r);
}int main(){
n=rd(),q=rd();for(int i=1;i<=n;i++)a[i]=rd(),b[i]=a[i];sort(b+1,b+1+n);cnt=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++){a[i]=lower_bound(b+1,b+1+cnt,a[i])-b;rt[i]=rt[i-1];c(rt[i],1,cnt,a[i]);}
for(int i=1,l,r,k;i<=q;i++){l=rd(),r=rd(),k=rd();wr(b[query(1,cnt,k,rt[l-1],rt[r])]),putchar('\n');}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号