并查集
并查集
突然发现不会并查集的按秩合并
只能爬回来补了。
UPD：2022/4/7
突然发现学的按秩合并是假的，实际上是启发式合并……
所以回来修锅。
定义
并查集是一种用于处理一些不相交的集合的合并与查询问题的树形数据结构
能够将两个集合合并 或者查询某个元素处于哪个集合中
用法
预处理
并查集维护的是一个森林，森林中的每棵树表示一个连通块。
因为一棵树中的所有祖先都是统一的，所以判断两个点是否在同一个连通块时只需判断这两个点的祖先是否相同即可。
朴素算法对于每个点，存下其祖先的值，如果查询，就一直递归找到其祖先即可。
一开始每个点的祖先都是其本身。
设 \(f_i\) 表示的是 \(i\) 的祖先。
void clear(){
for(int i=1;i<=n;i++)
f[i]=i;
}
查询
对于一个元素，只要不断递归就能找到其祖先了。
该点就是这棵树的根，相当于集合编号，树根的祖先就是其本身。
int cz(int x){
if(x==f[x])return x;
return cz(f[x]);
}
至于查询，就是判断两个元素的祖先是否相同即可。
bool pd(int x,int y){
if(cz(x)==cz(y))return true;
return false;
}
合并
至于合并，就是将一个节点的祖先改成另一个节点的祖先即可。
注意这里被合并的祖先的子树中所有点的祖先信息都还没有更新为另一个祖先
所以每一个想调用一个元素的祖先信息时一定要把它做一遍查询更新它祖先的值再去调用
void hb(int x,int y){
int a=cz(x),b=cz(y);
f[a]=b;
}
很明显如果树的形态是一条链，单次合并或是查询的时间复杂度就会退化成 \(O(n)\) 级别，所以要对算法进行优化。
优化
路径压缩
一般情况下常用的优化方法，写起来也非常简单。
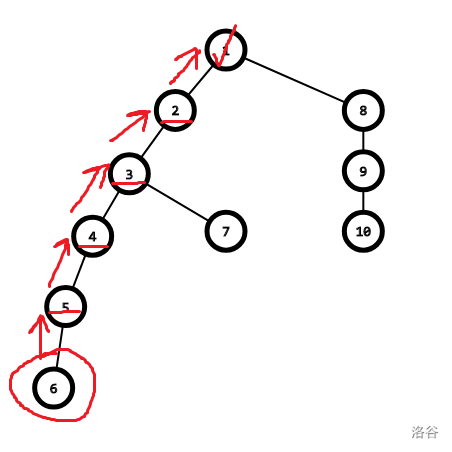
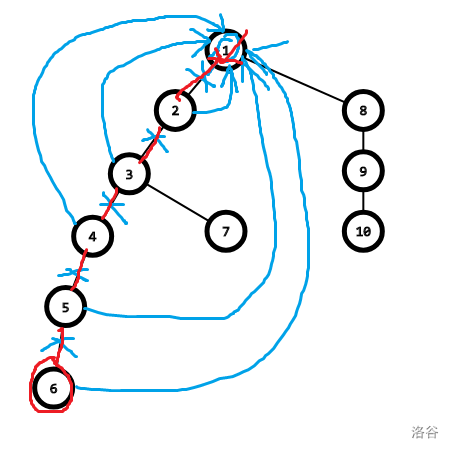
原理就是，因为对于每个连通块，只需要用到祖先的信息，所以在查询每个点的祖先时，直接将路径上的点的父亲编号 \(f_i\) 全都接到祖先上。
因为查找是递归实现的，所以路径上的每个点都能接到祖先上。
可以结合下图理解。
找祖先的过程：
对于路径上的点，全接到祖先：
路径压缩后的并查集：
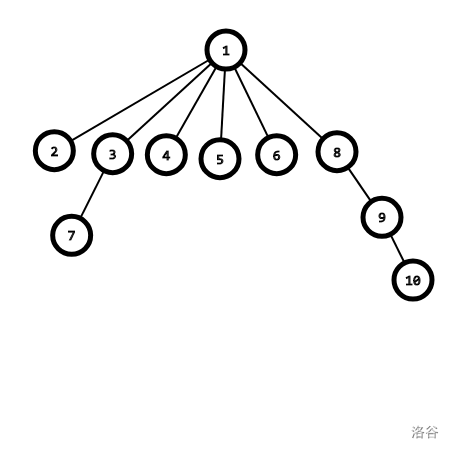
代码也比较简单，只要在递归的过程中改变父节点的值就行。
int cz(int x){
if(x==f[x])return x;
return f[x]=cz(f[x]);
}//下面的是用三目运算符的版本。
int cz(int x){return x==f[x]?x:f[x]=cz(f[x]);}
时间复杂度：
最坏情况下，时间复杂度为 \(O(m \log n)\)。
平均时间复杂度为 \(O(m \alpha(n))\)（\(\alpha(n)\) 可以看做常数）。
启发式合并
\(\color{Blue}{蒟蒻的启发式合并学习笔记}\)
虽然不常用，但是好像可撤销。
启发式合并就是每次合并时将元素个数少的集合并到元素多的集合上。
因为要比较连通块内元素个数，所以要用一个数组 \(size_i\)，初始化时为 1，合并时相加即可。
如果一开始所有集合都是只有一个元素的。
那么经过这样的合并后，从根节点往下走，每走一步子树大小至少减半。
这样可以保证合并的复杂度。
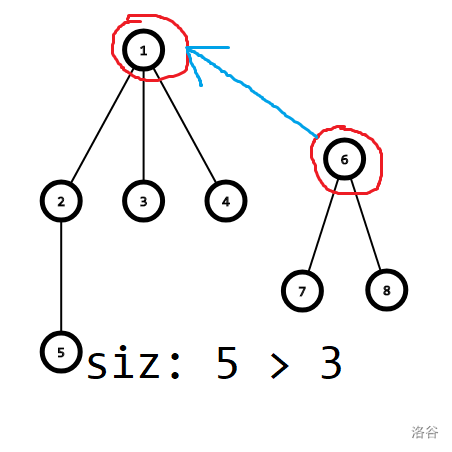
void hb(int x,int y){
int a=cz(x),b=cz(y);
if(a==b)return ;
if(si[a]>si[b])swap(a,b);
f[a]=b;si[b]+=si[a];
}
时间复杂度：\(O(m \log n)\)。
证明：
假设要合并的两个集合的子树大小分别为 \(x,y\)，深度分别为 \(h_1,h_2\)。
\(\because\) 只有被合并到下面的子树的深度才会 \(+1\)。
- 如果 \(x<y\)，那么子树的深度就变成 \(\max(h_1+1,h_2)\)
- 如果 \(h_2 \ge h_1+1\)，对于 \(y\) 来说，子树的深度没有发生变化。
- 如果 \(h_2 < h_1+1\)，那么树的深度 \(+1\)，但树的大小 \(size\) 变成 \(x+y\)。
\(\because y>x\)
\(\therefore x+y>2 \times x\)
\(\therefore size\) 至少翻倍。
- 如果 \(x \ge y\)，就直接 \(swap(x,y)\)，情况还是一样。
经过上面的分类讨论可以得出，启发式合并只有当 \(h_2<h_1+1\) 的情况下，树高 \(+1\)，子树大小 \(\times 2\)。
\(\because\) 子树大小最多翻倍 \(O(\log_2n)\) 次。
\(\therefore\) 启发式合并后的树高最高为 \(O(\log_2n)\)。
按秩合并
对于每一个集合定义一个 \(dep\) 数组，表示的是当前集合的树形结构的深度，初始值为 \(1\)。
在合并两个集合时，比较两个集合的深度大小，将深度小的集合合并到深度大的集合上。
因为这样做可以保证树的深度不会增加。
因为被接上去的树的深度 \(+1\)，但是深度大的树的深度肯定 \(\ge\) 深度小树的的深度 \(+1\)，所以没有影响。
比如上图中要合并两个集合，很明显，如果将 \(1\) 接到 \(4\) 上，树的深度不会发生改变。
这样可以保证树的深度不会超过 \(O(\log_2n)\)，所以 \(n\) 次查询的最劣复杂度是 \(O(n\log_2n)\)。
证明：
因为合并后的树高不会增加，除非两集合的树高相同，则被合并的树高 \(+1\)。
设：\(siz_h\) 表示的是合并产生树高为 \(h\) 的树，至少要 \(siz_h\) 个节点。
显然，如果想要合并得到一棵高为 \(h+1\) 的树，就需要合并两棵高为 \(h\) 的树。
所以 \(siz_{h+1} \ge 2 \times siz_h\)
边界是 \(siz_1=1\)，所以 \(siz_h=2^{h-1}\)。
由此可以得出，\(h\) 的最大值。
\(\because 2^{h-1}=n\)
\(\therefore h=\log_2n+1\)
证得按秩合并可以保证单次查询复杂度不超过 \(O(\log_2n)\)。
总结
并查集是简单的维护连通性的数据结构。
虽说并查集能做到的，LCT 也都行，但并查集更为简洁且更不易出错。
\(\color{White}{其实只是为了学可持久化并查集才补笔记的……}\)
