trie树学习笔记

一个巨大的坑

trie 树

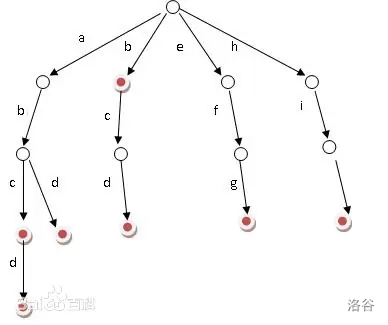
用于查找字符的数据结构。
典型的空间换时间。

定义

又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。 ———— 来自百度百科

建立

对于一个字符串，根据其原有的关系建 trie 树，对于相同前缀部分，会在不同处分叉。
根节点为空节点。
建树的操作是，如果没有节点，就新建一个节点，否则就走到节点上继续。

string s;
int len,t[N][26],tot,u,c,flag[N];
void insert(){
    cin>>s;len=s.length();u=0;
    for(int i=0;i<len;i++){
        c=s[i]-'a';
        u=t[u][c]?t[u][c]:t[u][c]=++tot;//如果无节点，就新建。 
    }flag[u]=1;//字符串末尾标记
}

查询

与建立的操作同理。
从根节点开始，根据字符串长度搜索，如节点为空直接跳出。

int search(){
    cin>>s;len=s.length();u=0;
    for(int i=0;i<len;i++){
        c=s[i]-'a';if(!t[u][c])break;
        u=t[u][c];
    }return flag[u];
}

复杂度

时间复杂度：对于一个长为 \(l\) 的字符串，插入或查询的时间复杂度均为 \(O(l)\)
空间复杂度：对于 \(n\) 个长分别为 \(l_i\)，字符集为 \(B\) 的字符串，所用的空间复杂度为 \(O(\sum_{i=1}^n l_i \times B)\)

模板题

Luogu P2580 于是他错误的点名开始了

• 先给定 \(n\) 个字符串
• 然后依次给出 \(m\) 个字符串，判断与之前出现的字符串的关系是：重复，正确还是错误。

做法

对于前面给出的字符串，建 trie 树，在结尾打上标记，标记初始值为 1。
查询时，如果结尾标记为 0，就是错误。
如果标记为 1，就是正确，并将标记修改为 2。
否则就是重复。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6;
int t[N][30],u,c,tot,len,n,m,f[N];string s;
void insert(){u=0;for(int i=0;i<len;i++){c=s[i]-'a';u=(t[u][c]?t[u][c]:t[u][c]=++tot);}f[u]=1;}
int check(){u=0;for(int i=0;i<len;i++){c=s[i]-'a';if(!t[u][c])return 0;u=t[u][c];}if(f[u]==1){f[u]=2;return 1;}return 2;}
int main(){
    cin>>n;for(int i=1;i<=n;i++)cin>>s,len=s.length(),insert();cin>>m;
    for(int i=1,g;i<=m;i++){cin>>s;len=s.length();g=check();if(g==0)puts("WRONG");else if(g==1)puts("OK");else puts("REPEAT");}
}