计算几何全家桶（一）

【一】：图形之间的位置关系

1.点与线段

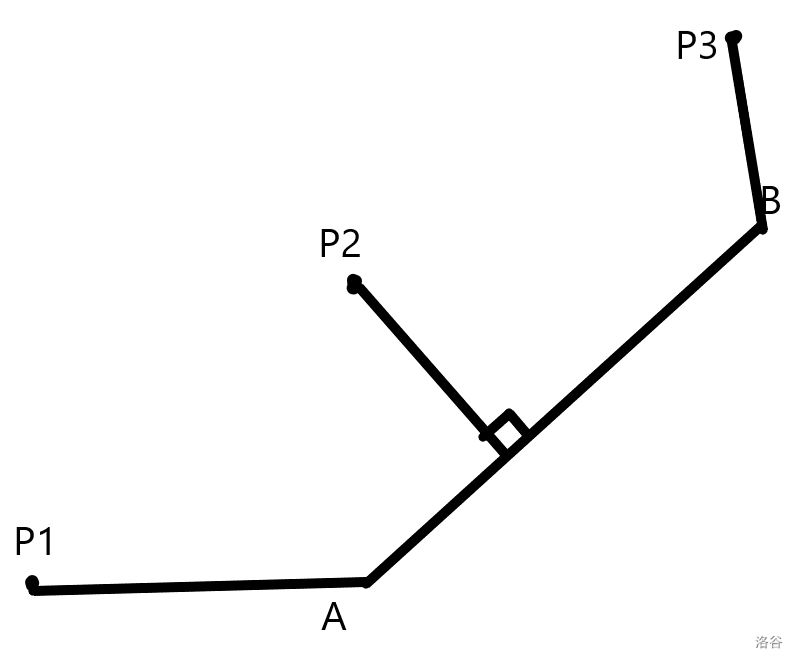
（一）：判断点是否在线段上

给定点 $P$，线段的端点 $A,B$，如果点 $P$ 在线段 $AB$ 上，则需满足 $\overrightarrow{PA}$ 与 $\overrightarrow{PB}$ 共线，且 $P$ 在 $\overrightarrow{AB}$ 之间。

bool check_xd(d p,d a,d b){//判断点 p 是否在线段 AB 上 
    return !jd(cj(p-a,b-a))&&jd(dj(p-a,p-b))<=0;
//用 len(p-a)+len(p-b)==len(a-b) 判断更为直观，但精度损失大
}//向量pa与pb共线且p在a,b之间 

（二）：求点到线段的距离

给定点 $P$，线段的端点 $A,B$，点到线段距离情况分三种。
第一种： 最近距离是线段 $PA$ 的长度
第二种： 最近距离是线段 $BP$ 的长度
第三种： 最近距离是点 $P$ 到线段 $AB$ 的垂直距离

dd dis_xd(d p,d a,d b){//点 P 到线段 AB 的距离 
    if(a==b)return len(p-a);//特判线段两端点重合的情况
    d x=p-a,y=p-b,z=b-a;//x:PA y:PB z:BA
    if(jd(dj(x,z))<0)return len(x);
    if(jd(dj(y,z))>0)return len(y);
    return ABS(cj(x,z)/len(z));//用叉积计算面积除底边长就是点到线段垂直距离 
}

2.点与直线

（一）：判断点是否在直线上

给定点 $P$，直线上的两点 $A,B$，则只需判断直线 $AP$ 与直线 $BP$ 共线即可。

bool check_zx(d p,d a,d b){//判断点 P 是否在直线 AB 上
    return !jd(cj(p-a,p-b));//PA,PB 共线
}

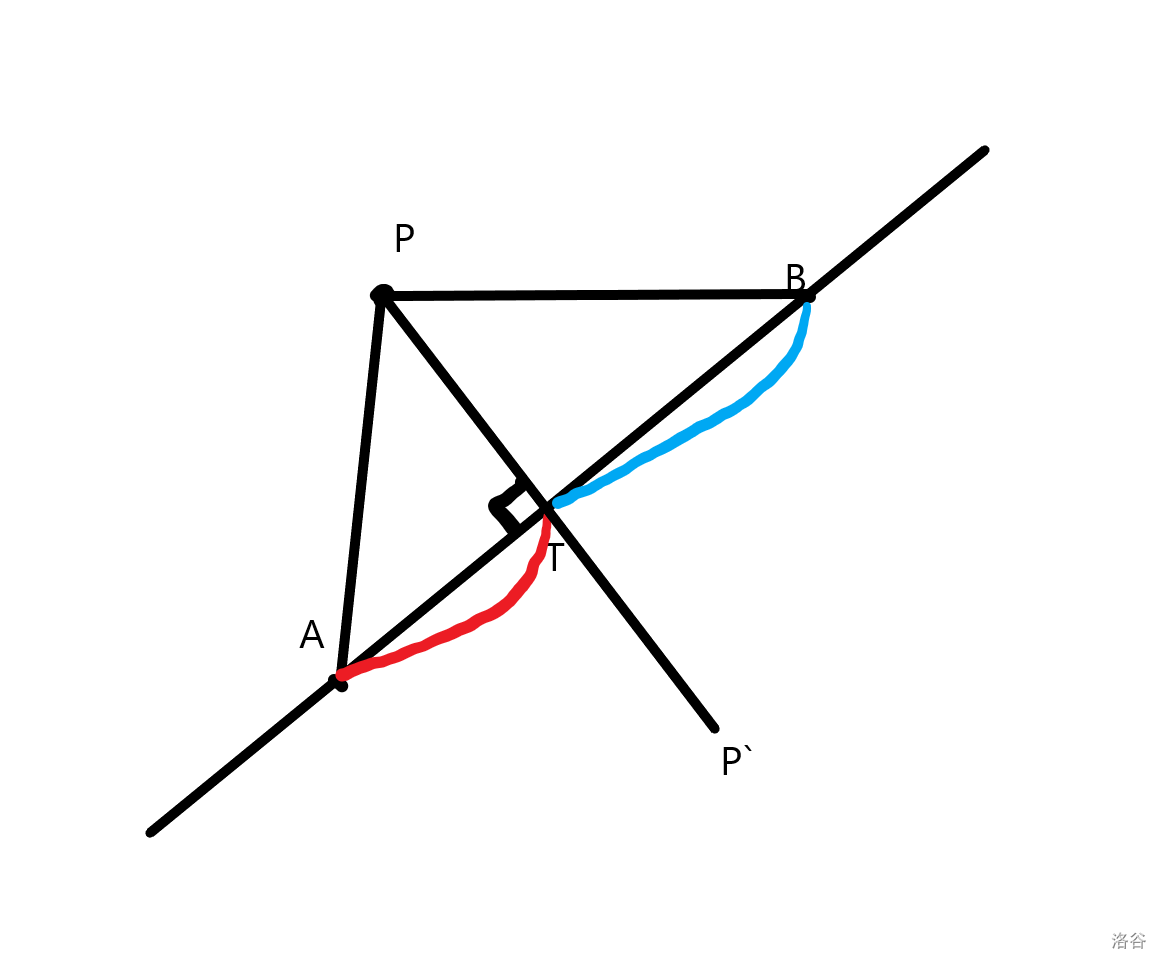
（二）：点到直线的垂足

给定点 $P$，直线上的两点 $A,B$，求点到直线的垂足。
首先表示出 $\overrightarrow{AP},\overrightarrow{BP},\overrightarrow{AB}$，然后分别求出 $\overrightarrow{AP},\overrightarrow{BP}$ 在 $\overrightarrow{AB}$ 上的投影长度也就是点积（图中红色和蓝色部分），就能求得垂足位置了。

d fd(d p,d a,d b){//点P到直线AB的垂足
    d x=p-a,y=p-b,z=b-a;
    dd len1=dj(x,z)/len(z),len2=-1.0*dj(y,z)/len(z);//分别计算AP,BP在AB,BA上的投影
    return a+z*(len1/(len1+len2));//点A加上向量AF
}

（三）：点关于直线的对称点

给定点 $P$，直线上的两点 $A,B$，求点关于直线的对称点。
很明显就是把上图的 $\overrightarrow{PF}$ 延长一倍。

d dcd(d p,d a,d b){//点P关于直线AB的对称点
    return p+(fd(p,a,b)-p)*2;//将PF延长一倍即可
}

3.线与线

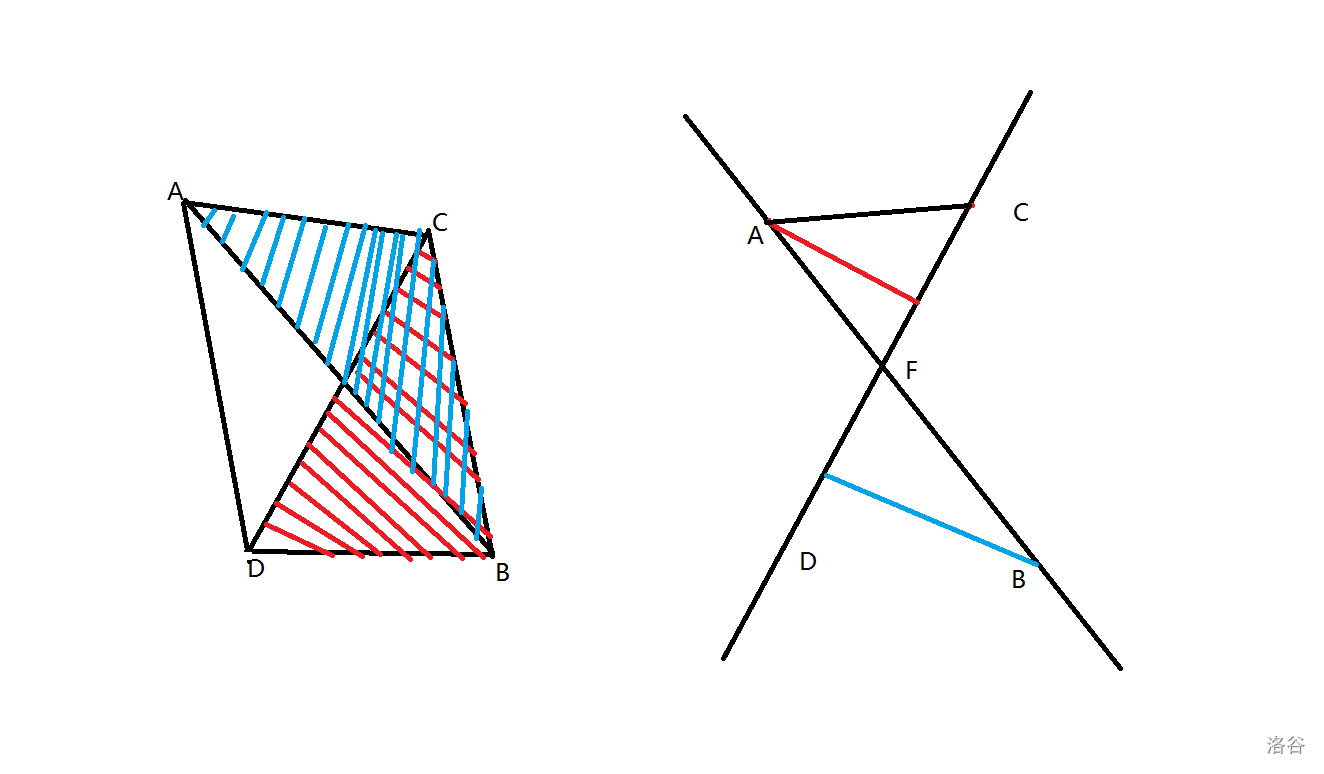
（一）：求两直线的交点

分别给定两直线上的两点，求两直线交点。
如上图中，要求的就是 $\overrightarrow{AF}$，可以先求出 $\frac{\left| \overrightarrow{AF} \right|}{\left| \overrightarrow{FB} \right|}$ ，也就是图中红色线段与蓝色线段长度比，而长度比很明显可以用叉积求面积比得出。

d cross_zx(d A,d B,d C,d D){//两直线AB,CD的交点
    d x=B-A,y=D-C,z=A-C;
    return A+x*(cj(y,z)/cj(x,y));//点A加上向量AF
}

（二）：判断线段与直线是否相交

分别给定直线上两点和线段端点，判断是否相交。
稍微转换一下思路：可以先求出两直线的交点，然后判断交点是否在线段上即可。
用到的函数之前都已列出。

bool check_zx_xd(d A,d B,d C,d D){//判断直线AB与线段CD是否相交
    return check_xd(cross_zx(A,B,C,D),C,D);//直线AB与直线CD的交点在线段CD上
}

（三）：判断两线段是否相交

如图中的线段 $AB,CD$，很明显要同时保证 $A,B$ 分别在直线 $CD$ 两侧且 $C,D$ 分别在直线 $AB$ 两侧。
判断的方法也是用叉积，即保证异号。

bool check_xd(d A,d B,d C,d D){//判断两线段AB,CD是否相交
    dd c1=cj(B-A,C-A),c2=cj(B-A,D-A);
    dd d1=cj(D-C,A-C),d2=cj(D-C,B-C);
    return jd(c1)*jd(c2)<0&&jd(d1)*jd(d2)<0;//分别在两侧
}

4.点与多边形

（一）：判断点是否在任意多边形内（射线法）

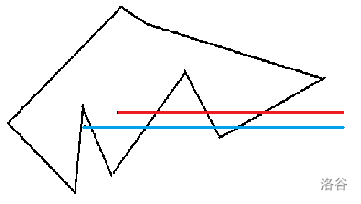
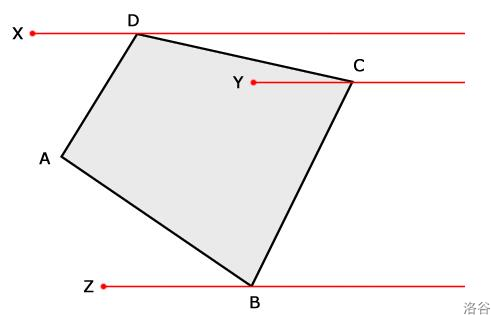
给定点 $P$ 和 $n$ 条边的多边形，判断点 $P$ 是否在多边形内部。
如果用射线法，时间复杂度是 $O(n)$，主要是由点 $P$ 为起点做一条射线，如果射线与多边形的交点个数为奇数个，说明点在多边形内部，否则在外部。
可以参考一下上面的图，如果一个点在多边形外部，以之为起点的射线最终必然在多边形外部，所以射线与多边形的交点个数必定为偶数个，可以类似于进去了必定还会出来。
然后就是要考虑到其中的一些特殊情况。

1. 点在多边形边上的情况，我是直接将这种情况直接归为一类。
2. 射线穿过多边形顶点的情况，对于这种情况比较难理解，可以看一下右上的图。

首先，线段与射线相交的条件是线段的两个端点在射线的两侧。
如果我们定义射线穿越的顶点属于某一侧，比如在图中规定射线经过的点均在射线的以上一侧。
所以图中射线 $Y$ 没有经过边 $CD$，但经过了 $CB$，所以在多边形内部。
图中射线 $X$ 同时经过了边 $AD,AC$，所以在多边形外部。
图中射线 $Z$ 没有与多边形相交，所以在多边形外部。

3. 射线与多边形的边重合的情况，很显然，对于这条重合的边的两个端点，都在射线以上的一侧，可以看做是射线没有穿过这条边来处理。

int PIP(d *P,int n,d a){//【射线法】判断点A是否在任意多边形Poly以内
    int cnt=0;dd tmp;
    for(int i=1;i<=n;i++){
        int j=i<n?i+1:1;
        if(check_xd(a,P[i],P[j]))return 2;//点在多边形上
        if(a.y>=min(P[i].y,P[j].y)&&a.y<max(P[i].y,P[j].y))//纵坐标在该线段两端点之间
            tmp=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x),cnt+=jd(tmp-a.x)>0;//交点在A右方
    }return cnt&1;//穿过奇数次则在多边形以内
}

（二）：判断点是否在凸多边形内（二分法）

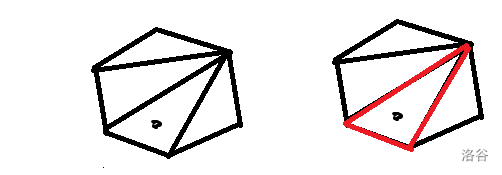
二分法判断的步骤：

1. 选择多边形的一个点为起点，连接其他点作射线。
2. 判断给定的点是否在所有射线包围的区域之内。
3. 二分找到正好包夹当前点的两条射线。
4. 判断给定点在这条边的左方还是右方，由此判断给定点是否在三角形区域内，也就是是否在多边形内。

bool judge(d a,d L,d R){//判断AL是否在AR右边
    return jd(cj(L-a,R-a))>0;//必须严格以内
}
int PIP_(d *P,int n,d a){//【二分法】判断点A是否在凸多边形Poly以内
    //点按逆时针给出
    if(judge(P[1],a,P[2])||judge(P[1],P[n],a))return 0;//在P[1_2]或P[1_n]外
    if(check_xd(a,P[1],P[2])||check_xd(a,P[1],P[n]))return 2;//在P[1_2]或P[1_n]上
    int l=2,r=n-1;
    while(l<r){//二分找到一个位置pos使得P[1]_A在P[1_pos],P[1_(pos+1)]之间
        int mid=l+r+1>>1;
        if(judge(P[1],P[mid],a))l=mid;
        else r=mid-1;
    }
    if(judge(P[l],a,P[l+1]))return 0;//在P[pos_(pos+1)]外
    if(check_xd(a,P[l],P[l+1]))return 2;//在P[pos_(pos+1)]上
    return 1;
}

5.线与多边形

（一）：判断线段是否在任意多边形中

线段两端点均在多边形中且线段与多边形的边没有相交。

（二）：判断线段是否在凸多边形中

线段两端点均在多边形中即可。

6.多边形与多边形

判断两个多边形是否相离

属于不同多边形的任意两边都不相交，且其中一个多边形上的任意点都不被另一个多边形所包含。
使用射线法和二分法的时间复杂度分别为 $O(n^3),O(n^2\log_2n)$

bool judge_PP(d *A,int n,d *B,int m){//判断多边形A与多边形B是否相离
    for(int i=1;i<=n;i++){
        int g=i<n?i+1:1;
        for(int j=1;j<=m;j++){
            int h=j<m?j+1:j;
            if(cross_xd(A[i],A[g],B[j],B[h]))return 0;//两线段相交
            if(PIP(B,m,A[i])||PIP(A,n,B[j]))return 0;//点包含在内
        }
    }return 1;
}

【二】：图形面积

1.任意多边形面积

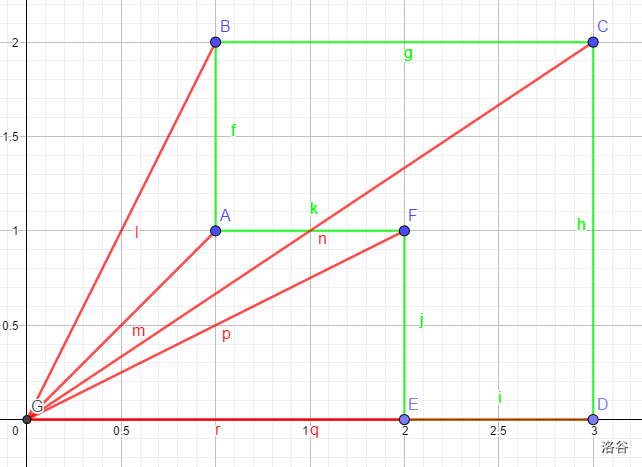
对于图中情况，有：

$$S_{ABCDEF}=-S_{\vartriangle OAB}+S_{\vartriangle OBC}+S_{\vartriangle OCD}-S_{\vartriangle ODE}-S_{\vartriangle OEF}-S_{\vartriangle OFA}$$

所以很明显可以用叉积计算。通式就是： $$\dfrac{\sum_{i=1}^{cnt-1} p_i \times p_{i+1}}{2}$$

dd Polyarea(d *P,int n){//任意多边形P的面积
    dd s=0;
    for(int i=1;i<=n;i++)s+=cj(P[i],P[i<n?i+1:1]);
    return s/2.0;
}

2.圆的面积并

不会，咕咕咕

3.三角形的面积并

不会，咕咕咕