P3187

problem

给定 \(n\) 个点的坐标，求能够覆盖所有点的最小面积的矩形，输出所求矩形的面积和四个顶点坐标。

solution

感性理解可知最小覆盖矩形的一条边肯定与凸包的一条边重合。很明显是先跑出凸包然后旋转卡壳维护每个向量最上、最左、最右的点，并更新答案。

但是维护的过程很繁琐。

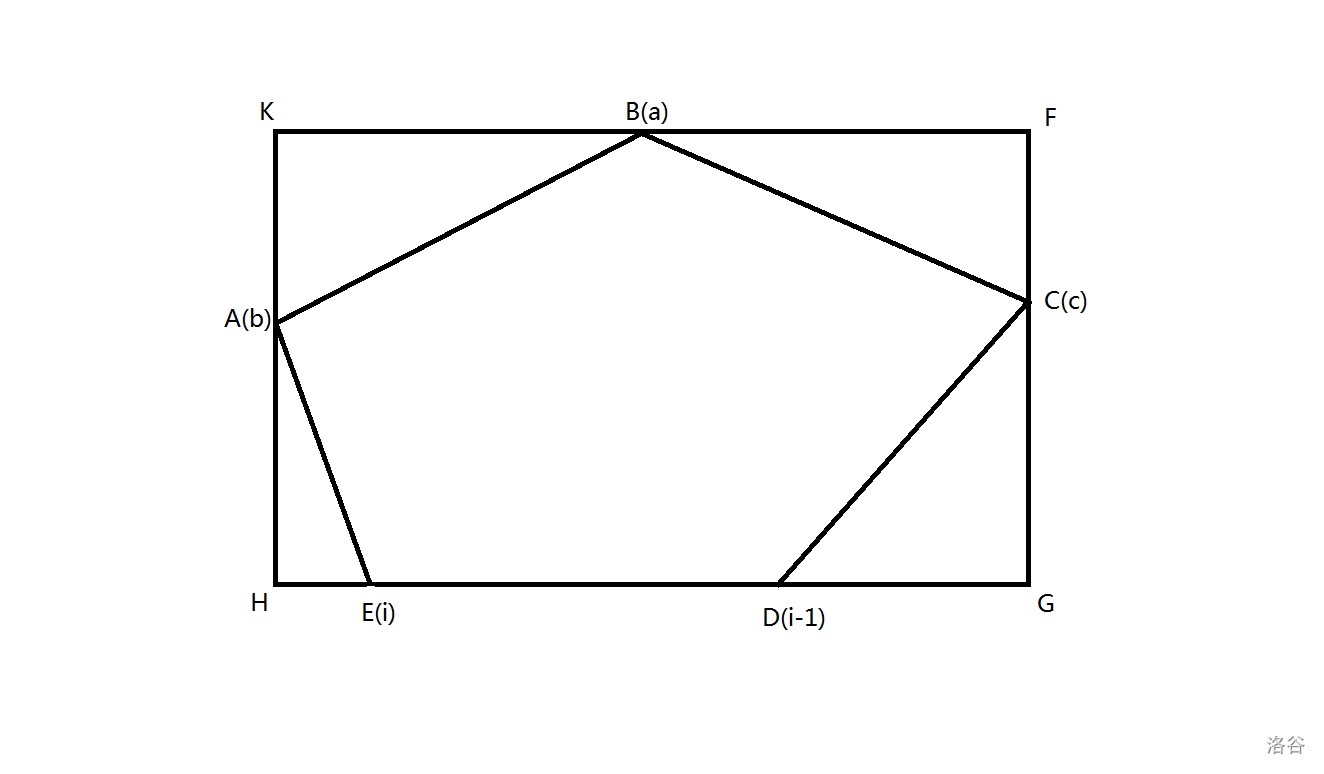
假设每个点最上、最左、最右的点指针分别为 \(a,b,c\)，\(\theta\) 表示两向量之间的夹角大小，用 \(\vec{x} \cdot \vec{y}\) 表示两个向量的点积，即 \(\vec{x} \cdot \vec{y} = \left| \vec{x} \right| \left| \vec{y} \right| \cos \theta\)，用 \(\vec{x} \cdot \vec{y}\) 表示两个向量的叉积，即 \(\vec{x} \times \vec{y} = \left| \vec{x} \right| \left| \vec{y} \right| \sin \theta\)

• 对于某个向量的最上的点，就像旋转卡壳的板子那样用叉积判断。

因为两个向量的叉积能够用来计算以其为邻边的平行四边形的面积。

如比较上图中 \(\overrightarrow{DE} \times \overrightarrow{AE}\) 与 \(\overrightarrow{DE} \times \overrightarrow{BE}\) 的大小，即可知对于向量 \(\overrightarrow{DE}\)，点 \(B\) 相对于点 \(A\) 更上，所以此时指针更新到 \(B\)。

• 对于某个向量的最左和最右的点，则要用点积判断。

因为两个向量的点积能够用于计算向量端点的 \(x\) 轴上的距离。

比如图中的 \(\overrightarrow{DE} \cdot \overrightarrow{AE}\)，其值为 \(\left| \overrightarrow{DE} \right| \left| \overrightarrow{HE} \right|\)，而 \(\left| \overrightarrow{HE} \right|\) 正好是当前向量到点 \(A\) 的 \(x\) 轴上的距离。

再比如图中的 \(\overrightarrow{ED} \cdot \overrightarrow{CD}\)，其值为 \(\left| \overrightarrow{ED} \right| \left| \overrightarrow{DG} \right|\)，而 \(\left| \overrightarrow{DG} \right|\) 正好是当前向量到点 \(C\) 的 \(x\) 轴上的距离。

要注意这里求出来的点积要除以当前向量的长度。

• 矩形的面积可以用之前在旋转卡壳时的数据求出。

以图中情形为例。

矩形的长就是 \(\dfrac{\overrightarrow{DE} \cdot \overrightarrow{AE} + \overrightarrow{ED} \cdot \overrightarrow{CD}}{\left| \overrightarrow{ED} \right| } + \left| \overrightarrow{ED} \right|\)。

矩形的高就是 $\dfrac{\overrightarrow{DE} \times \overrightarrow{BE}}{\left| \overrightarrow{ED} \right|} $。

• 然后是如何求矩形四个点的坐标。

比如求图中的 \(G\) 点坐标，其实就是点 \(D\) 的坐标加上向量 \(\overrightarrow{DG}\)，具体如何求 \(\overrightarrow{DG}\) 可以看前面。

最后就是精度问题，此题没有 SPJ，为了防止输出 -0.00000，得特判一下。

code

#include <bits/stdc++.h>
using namespace std;
const int N=1e5;const double eps=1e-8;
struct d{double x,y;d(double a=0,double b=0):x(a),y(b){}}p[N],s[N],q[N];
int n,tp,id;typedef d vec;double k1,k2;
vec operator+(vec a,vec b){return vec(a.x+b.x,a.y+b.y);}vec operator-(d a,d b){return vec(a.x-b.x,a.y-b.y);}
vec operator*(vec a,double p){return vec(a.x*p,a.y*p);}vec operator/(vec a,double p){return vec(a.x/p,a.y/p);}
double dis(d a){return sqrt(a.x*a.x+a.y*a.y);}void kj(int a){if(fabs(s[a].x)<=eps)s[a].x=0;if(fabs(s[a].y)<=eps)s[a].y=0;}
double cj(d a,d b){return a.x*b.y-a.y*b.x;}double dj(d a,d b){return a.x*b.x+a.y*b.y;}
bool cmp(d a,d b){k1=atan2((a.y-p[1].y),(a.x-p[1].x));k2=atan2((b.y-p[1].y),(b.x-p[1].x));if(k1==k2)return a.x<b.x;return k1<k2;}
void xzqq(){
    double ans=1e114,l,r,h,e,len;int a=2,b=2,c=2;
    for(int i=1;i<=tp;i++)s[i+tp]=s[i];
    for(int i=2;i<=tp+1;i++){
	while(cj(s[a]-s[i],s[i-1]-s[i])<=cj(s[a+1]-s[i],s[i-1]-s[i]))a++;
	while(dj(s[b]-s[i],s[i-1]-s[i])>=dj(s[b+1]-s[i],s[i-1]-s[i]))b++;
	if(i==2) c=a;while(dj(s[c]-s[i-1],s[i]-s[i-1])>=dj(s[c+1]-s[i-1],s[i]-s[i-1]))c++;
	len=dis(s[i]-s[i-1]);l=dj(s[c]-s[i],s[i-1]-s[i])/len;r=dj(s[b]-s[i-1],s[i]-s[i-1])/len;
	h=cj(s[i]-s[i-1],s[i]-s[a])/len;l=fabs(l);r=fabs(r);h=fabs(h);e=(l+r-len)*h;
	if(e<ans){
	    ans=e;q[1]=s[i]-(s[i]-s[i-1])*(l/len);q[2]=q[1]+(s[i]-s[i-1])*((r+l-len)/len);
            q[3]=q[2]+(s[b]-q[2])*(h/dis(s[b]-q[2]));q[4]=q[3]+(s[i-1]-s[i])*((r+l-len)/len); 
	}
    }printf("%.5lf\n",ans);
}int main(){
    cin>>n;for(int i=1;i<=n;i++){
	scanf("%lf%lf",&p[i].x,&p[i].y);if(i==1)continue;
	if(p[i].y<p[1].y||(p[i].y==p[1].y&&fabs(p[i].x)<fabs(p[1].x)))swap(p[1],p[i]);
    }sort(p+2,p+1+n,cmp);s[tp=1]=p[1];
    for(int i=2;i<=n;i++){while(tp>1&&cj(s[tp]-s[tp-1],p[i]-s[tp])<=0)tp--;s[++tp]=p[i];}xzqq();
    q[0].y=1e9;for(int i=1;i<=4;i++)if(q[i].y<q[id].y||(q[i].y==q[id].y&&q[i].x<q[id].x))id=i;
    for(int i=1;i<=4;i++)kj(i);printf("%.5lf %.5lf\n",q[id].x+eps,q[id].y+eps);    
    for(int i=0;i<3;i++)printf("%.5lf %.5lf\n",q[(i+id)%4+1].x+eps,q[(i+id)%4+1].y+eps);return 0;
}