manacher算法学习笔记

manacher算法求最长回文串

模板题：

P3805 【模板】manacher 算法

给定一个仅有小写字母的字符串 \(S\)，求 \(S\) 中最长回文串，字符串长为 \(n\)。

\(n \le 1.1*10^7\)

分析：

最暴力的方法是直接枚举所有可能的 \(l,r\),对于每一对 \(l,r\) 暴力判断其是否为回文串，记录其中的最长回文串长度。这样做的时间复杂度是 \(O(n^3)\)，好TM优秀

这种暴力做法的优化也很简单，如果一个回文子串的长度是奇数，那么这个回文子串以中间的字符为对称轴对称；如果长度是偶数，就以最中间两个字符之间的间隙为对称轴对称。
所以我们可以遍历这些对称轴，在每个对称轴上同时向左右两边遍历，直到左右字符不同或到达边界。
这样做的时间复杂度为 \(O(n^2)\),我是没听说过有n方过千万这回事，但也过不去。

很明显，此题需要达到 \(O(n)\) 的时间复杂度才能通过，所以要对 \(O(n^2)\) 的暴力算法进行改进。

manacher算法

相比于 \(O(n^2)\) 暴力算法的改进：

1. 回文子串的对称轴可能是中间的一个字符，也有可能是中间两个字符之间的间隙，对这两种情况分开处理。
   可以在原先字符串的每两个字符之间插入一个不会出现的字符，形成一个新的字符串。
   这样就可以以新字符串内的每一个字符为对称轴进行遍历了。
   这个预处理部分的代码：

string s;
void init(){
    int m=0;s[m++]='~';//新字符串开头要用另一个字符因为暴力拓展左右两侧,当下标为0时，由于s[0]是'~'，自动停止。故不会下标溢出。 
    for(int i=0;i<n;i++)s[m++]=ch[i],s[m++]='#';
    s[m++]='#';//在每两个字符之间插入'#' 
}

2. 因为会有很多子串被重复访问，导致时间效率降低。
   所以要使用之前已有的信息对算法进行优化。
   数组 \(len\),其中 \(len_i\) 表示在第 \(i\) 位时的回文子串拓展长度。
   变量 \(mx\),表示遍历到的最右边的节点下标。
   变量 \(mid\),表示右端点遍历到 \(mx\) 的回文子串的对称轴所在节点下标。

manacher算法实现流程：

从下标 \(i=1\) 开始遍历新字符串。
在某个节点时，会产生两种情况：

• 情况一：如果此时 \(i \ge mx\)，此时直接向外暴力匹配，并且同时更新\(mx\)和\(mid\)的值即可。

• 情况二：如果此时 \(i < mx\),设 \(i^\prime\) 是\(i\)关于\(mid\)的对称点,此时又要再分成三种情况讨论：
  构建如图所示的图形：
  

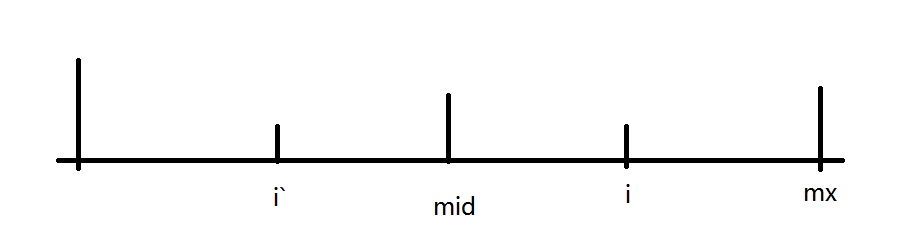
• 情况二的分支1：如果以 \(i^\prime\) 为对称轴的回文子串在以\(mid\)为对称轴的回文子串内部，即：\(i+len_{i^\prime}<mx\),因为在左右端点内的子串是满足回文的，所以\(i\)为对称轴的回文子串和 \(i^\prime\) 为对称轴的回文子串是关于\(mid\)对称的。
  如下图：
  

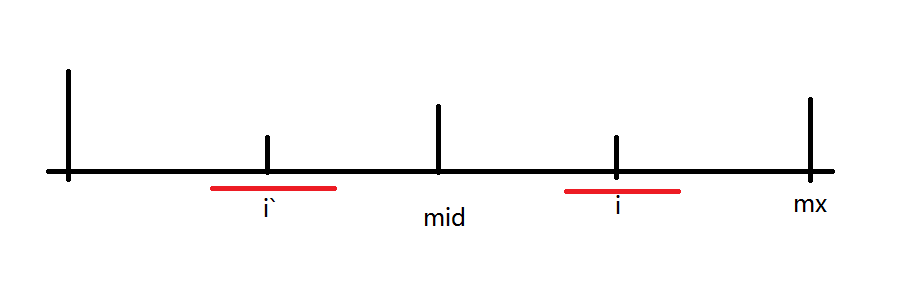
• 情况二的分支2：如果以 \(i^\prime\) 为对称轴的回文子串的左端点超过了以 \(mid\) 为边界的回文子串的左端点，此时以\(i\)为对称轴的回文子串长度确认为 \(mx-i\),因为如果以 \(i\) 为对称轴的回文子串的右端点超出 \(mx\) 的范围，这样结合产生的回文子串会比当前以 \(mid\) 为对称轴的回文子串要长，与“以 \(mid\) 为对称轴，\(mx\) 为右端点的回文子串是以 \(mid\) 为对称轴的最长回文子串”的前提条件矛盾。
  如下图：
  

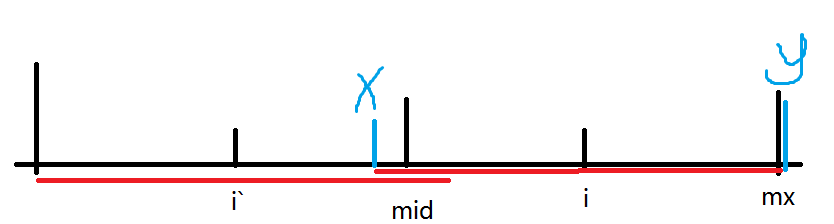
• 情况二的分支3：如果以 \(i^\prime\) 为对称轴的回文子串的左端点正好与以 \(mid\) 为边界的回文子串左端点重合，此时需继续向后匹配。
  因为边界重合，所以以 \(i\) 为对称轴的回文子串已知部分与 \(i^\prime\) 相同，设左右边界的下标分别为 \(x,y\),然后向外匹配即可。
  如下图：
  

以上流程的代码：

int manacher(){
len[0]=0;
for(int i=1;i<l;i++){
    if(i<mx)  len[i]=min(len[mid*2-i],mx-i);//对应第二种情况,赋值为  以i对应的i'的回文半径  和  i到mx的距离  中的较小值。
    else    len[i]=1;//对应第一种情况,直接赋值为初始值1暴力匹配 
    while(S[i-len[i]]==S[i+len[i]])len[i]++;//取最小值后开始从边界暴力匹配，匹配失败就直接退出
	if(len[i]+i>mx)	mx=len[i]+i,mid=i,maxn=max(maxn,len[i]);//更新变量
    }return (maxn-1);/*关于这里为什么要return sum-1,因为新字符串的长度和原字符串不同
所以这里得到的最大回文半径其实是原字符串的最大回文子串长度加1 (可以自己找个样例手推一下)*/
}

总结：
manacher算法的流程概括一下就是：先匹配 \(\Rightarrow\) 通过判断\(i\)与\(mx\)的关系进行不同的分支操作 \(\Rightarrow\) 继续遍历直到遍历完整个字符串。

算法的时间复杂度：

manacher求出最长回文子串的时间复杂度为 \(O(n)\),下面给出简要证明：

• 首先情况一的时间复杂度为 \(O(n)\) 的线性复杂度。
• 情况二的前两种分支都是 \(O(1)\) 复杂度。
• 对于第三种分支，可能会出现 \(O(1)\) 的时间复杂度，因为无法从\(mx\)继续向后匹配；也可能出现 \(O(n)\) 的复杂度，因为继续向后暴力匹配的复杂度是线性的。
• 两种需线性复杂度的情况都会更新 \(mx\) 的值，所以综合起来，manacher的时间复杂度是线性的，即 \(O(n)\) 。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+2e6;
char A[N],S[N<<1];
int maxn,mid,mx,l,len[N<<1],k,j;
void init(){
    S[0]='~';for(int i=0;i<j;i++)	S[++k]='#',S[++k]=A[i];
    S[++k]='#';l=k;
}int manacher(){
    len[0]=0;
    for(int i=1;i<l;i++){
	if(i<mx)	len[i]=min(len[mid*2-i],mx-i);
	else	len[i]=1;
	while(S[i-len[i]]==S[i+len[i]])len[i]++;
	if(len[i]+i>mx)	mx=len[i]+i,mid=i,maxn=max(maxn,len[i]);
    }return (maxn-1);
}int main(){
    scanf("%s",A);j=strlen(A);init();
    cout<<manacher()<<endl;return 0;
}

练习题：

P1659 [国家集训队]拉拉队排练：简单的最长回文子串题，但最后一个测试点需用到快速幂。
P6216 回文匹配:最长回文子串、字符串匹配、前缀和知识的综合应用，有一定的思维难度。