GSS系列中线段树部分的学习笔记

GSS系列中的线段树题目笔记

前言：

GSS系列也是线段树的一部分好题了。
其中GSS6和GSS8貌似是平衡树，所以将来单独另写笔记。
GSS7是树链剖分，也不在这篇博客中提及。

GSS系列题

这篇博客有多处借鉴网上资料，如侵删。

GSS1

GSS1

题意：

给一段序列（不一定是正整数），支持查询最大子段和。

题解：

线段树维护：区间和、区间最大子段和、区间最大前缀和、区间最大后缀和。

• 区间最大子段和：因为题目要求。
• 区间最大前缀和与最大后缀和：因为在合并两个区间时，合并后区间的最大子段和可以分成两种情况，一种是不跨过区间，就是左右儿子的最大子段和；另一种是跨过区间，最大子段和就是左儿子的区间最大后缀和与右儿子的区间最大前缀和之和，然后取三者中的最大值。
• 区间和：因为要维护区间最大前缀和和最大区间后缀和，所以也要分情况讨论。比如合并后区间的区间最大前缀和就要分两种情况讨论，一种是继承左儿子的最大前缀和；另一种是左儿子的区间和与右儿子的区间最大前缀和之和。

代码：

点击查看代码

#include <bits/stdc++.h>
#define lc p<<1
#define rc p<<1|1
using namespace std;
int rd(){
    int f=1,x=0; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
    while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=getchar();
    return f*x;
}
const int N=6e6;
int n,m,x,y;
struct tree{int l,r,sum,ls,rs,ps;}s[N];
void pushup(int p)
{
	s[p].sum=s[lc].sum+s[rc].sum;
	s[p].ps=max(s[lc].ps,max(s[rc].ps,s[lc].rs+s[rc].ls));
	s[p].ls=max(s[lc].ls,s[lc].sum+s[rc].ls);
	s[p].rs=max(s[rc].rs,s[rc].sum+s[lc].rs);
}
void build(int p,int l,int r)
{
	s[p].l=l;s[p].r=r;
	if(l==r){s[p].ls=s[p].ps=s[p].rs=s[p].sum=rd();return ;}
	int mid=(l+r)>>1;build(lc,l,mid);build(rc,mid+1,r);pushup(p);
}
tree query(int p,int l,int r)
{
	if(s[p].l>=l&&s[p].r<=r)	return s[p];int mid=(s[p].l+s[p].r)>>1;
	if(l>mid)	return query(rc,l,r);
	else if(r<=mid)	return query(lc,l,r);
	else
	{
		tree ans,a=query(lc,l,r),b=query(rc,l,r);
		ans.sum=a.sum+b.sum;ans.ps=max(a.ps,max(b.ps,a.rs+b.ls));
		ans.ls=max(a.ls,a.sum+b.ls);ans.rs=max(b.rs,b.sum+a.rs);
		return ans;
	}
}
int main()
{
	n=rd();build(1,1,n);m=rd();
	while(m--){x=rd();y=rd();cout<<query(1,x,y).ps<<endl;}return 0;
}

GSS2

题意：

给出长度为\(n\)的序列\(a\)，\(q\)次询问，求最大子段和，相同的数只算一次。

题解：

因为相比于GSS1要求相同的数只算一次，所以GSS1中线段树直接维护区间最大子段和的操作不可取。
这道题其实类比P1972 [SDOI2009]HH的项链,之间有很多相似之处，然后从中得出此题的解法。

• 首先，这两题都是询问一个区间，没有修改操作，所以考虑离线，将所有查询按照右区间排序。
• 然后，这两题都要求相同的只算一次，因此利用前缀和的思想，用一个\(lst\)数组，统计某个数值\(a_i\)上一次在哪个位置出现过。如果未出现过，就修改之前的全部区间 ，否则修改\(lst_{a_i}+1\)与\(i\)之间的区间。

但这道题和HH的项链有一个很大的改变，HH的项链中每个值的贡献固定为1，所以只需简单的单点修改和区间查询就行了；但这道题中每个值的贡献不同，所以只是维护区间和不足以解决此题，还需维护区间历史最值。这就又牵涉到另一题P4314 CPU监控，其中线段树维护区间历史最值的方法也可以套用到这道题上。

基本思路有了就可以继续想出具体的做法：
线段树维护什么？
参考CPU监控这道题，线段树维护2个值：

1. 区间最大值ma
2. 之前区间的历史最大值hma

比如说我们扫描到\(i\)时的更新，就是相当于更新线段树上的\(\left[lst_{a_i}+1,i\right]\)之间的区间，然后处理\(q.r=i\)的询问，答案必然是\(\max( x.ma \mid q.l \le x \le q.r)\),但在此题中我们维护的线段树实际上是区间套区间，如果只维护最大值相当于只能取到在右端点\(r\)的值，但最大值不一定在右端点\(r\),所以还要记录这个过程中的最大值。

需要什么懒标记？

1. 为维护区间最大值，需一个当前区间的加法懒标记tag
2. 为维护区间历史最大值，需一个当前区间的历史最大加法懒标记htag

如何合并和维护？
对于区间最大值ma和维护区间最大值的懒标记tag,像普通线段树那样合并和更新即可。
区间历史最大值hma在合并时也取最大值，更新时取其与当前区间最大值与历史最大懒标记之和中的最大值。

pushup的代码：

void pushup(int p)
{
    s[p].ma=max(s[lc].ma,s[rc].ma);
    s[p].hma=max(s[lc].hma,s[rc].hma);//区间最大和历史最大取左右儿子max
}

在pushdown和update时一定要注意更新顺序对结果的影响。（本人就在这出锅了）
pushdown的代码：

void pushdown(int p){
    if(s[p].tag||s[p].htag){
        s[lc].hma=max(s[lc].hma,s[lc].ma+s[p].htag);
        s[rc].hma=max(s[rc].hma,s[rc].ma+s[p].htag);
	s[lc].ma+=s[p].tag;
        s[rc].ma+=s[p].tag;//先更新历史最大值，再更新区间最大值
	s[lc].htag=max(s[lc].htag,s[p].htag+s[lc].tag);
	s[rc].htag=max(s[rc].htag,s[p].htag+s[rc].tag);
	s[lc].tag+=s[p].tag;
	s[rc].tag+=s[p].tag;//对于懒标记也是先更历史最大懒标记
	s[p].tag=s[p].htag=0;//清空懒标记
    }
}

pushdown中s[lc].hma=max(s[lc].hma,s[lc].ma+s[p].htag);和s[rc].hma=max(s[rc].hma,s[rc].ma+s[p].htag);没有都用历史最大值来更新的原因是这样会让连续子段和不连续。
update的代码（核心部分）：

s[p].ma+=k;
s[p].hma=max(s[p].hma,s[p].ma);//注意这里因为s[p].ma已经更新过了，所以在更新s[p].hma时不要再把k加上
s[p].tag+=k;
s[p].htag=max(s[p].htag,s[p].tag);//懒标记同理
return ;

主函数如何操作？
首先，因为输入的序列\(a\)中有负数，所以初始预处理的代码如果写成这样：

for(int i=1;i<=n;i++){
    cin>>a[i];
    lst[i]=pre[a[i]];
    pre[a[i]]=i;
}

就会连样例过不去，因为用了负数作为数组下标。
解决方法很简单，就是\(lst\)和\(pre\)这两个数组开双倍空间，然后下标加上题目给出的界限即可。

for(int i=1;i<=n;i++){
    cin>>a[i];
    lst[i]=pre[a[i]+N];
    pre[a[i]+N]=i;
}

再用结构体存储询问，以\(r\)为关键字从小到大排序。

for(int i=1;i<=m;i++){
    cin>>q[i].l>>q[i].r;
    q[i].id=i;
}
sort(q+1,q+1+m,cmp);

在进行操作前先建一棵空树，里面什么都不存。

然后从左到右扫描\(i\),并更新\(\left[lst_{a_i}+1,i\right]\)之间的节点，用\(a_i\)的值。
同时更新满足\(q.r==i\)的询问的答案，也就是查询\(\left[q.l,q.r\right]\)区间的的历史最大值。
这个部分的代码：

int j=1;
for(int i=1;i<=n;i++){
    update(1,lst[i]+1,i,a[i]);
    for(j;j<=m&&q[j].r<=i;j++)
	ans[q[j].id]=query(1,q[j].l,q[j].r).hma;
}

最后按顺序输出答案即可。
完整代码链接

GSS3

题意：

\(n\) 个数，\(q\) 次操作,支持单点修改和区间最大子段和查询。

题解：

题目要求很明显，线段树维护区间最大子段和。难点在于如何合并左右区间。

合并时，最大子段和有两种情况：

1. 合并后节点的最大子段没有经过中心，这样就是左右儿子的最大子段和中的较大值。
2. 合并后节点的最大子段经过了中心，则最大子段和还可以由左右儿子从中间开始的最大值合并而成。

所以，线段树维护以下内容：

• 区间和
• 左起区间最大子段和与右起区间最大子段和
• 区间最大子段和。

因为是单修，所以无需懒标记。其他均为线段树模板操作，不再赘述。

pushup部分的代码：

点击查看代码

void pushup(int pos){
    s[pos].tot=s[lc].tot+s[rc].tot;
    int mid=(s[pos].l+s[pos].r)/2;
    s[pos].sum=max(s[lc].sum,max(s[rc].sum,s[lc].rsum+s[rc].lsum));
    s[pos].lsum=max(s[lc].lsum,s[lc].tot+s[rc].lsum);
    s[pos].rsum=max(s[rc].rsum,s[rc].tot+s[lc].rsum);
}

GSS系列中不可多得的水题。

完整代码

GSS4

题意：

给定有\(n\)个数字的序列\(a\),保证\(\sum_{i=1}^na_i \le 10^{18}\)
要求区间开平方和查询区间和的操作。

题解：

题目只要求维护区间和，所以重点在区间开平方的操作。
首先可以尝试一下，即便是\(10^{18}\)的极限数据，也只需六次开平方的操作就会变成\(1\)，而\(1\)的平方根就是本身。
很明显可以暴力单点修改，记录区间最大值，如果区间最大值\(\le 1\)，说明此区间开平方后与之前不会改变，退出即可。否则在递归到叶子结点时对其进行开平方。
因为是单点暴力修改，所以维护区间和不需要懒标记。
区间开平方的代码如下：

点击查看代码

void change(int p,int l,int r){
    if(s[p].l==s[p].r){s[p].Maxx=s[p].sum=(int)sqrt(s[p].sum);return ;}
    int mid=(s[p].l+s[p].r)>>1;
    if(l<=mid&&s[lc].Maxx>1)	change(lc,l,r);
    if(r>mid&&s[rc].Maxx>1)	change(rc,l,r);
    pushup(p);
}

其余都是线段树的模板操作。

GSS3和GSS4都好水

完整代码（因为此题卡常，所以代码不是特别简洁）

GSS5

毒瘤题

题意：

给定一个长度为\(n\)的序列，\(m\)次询问，每次询问要求查询左端点在\(\left[x_1,y_1 \right]\)之间，且右端点在\(\left[x_2,y_2 \right]\)之间的最大子段和，不保证区间不重合。
即：给出序列和\(l_1\),\(r_1\),\(l_2\),\(r_2\),求

\[\max\limits_{l_1 \le l \le l_2,r_1 \le r \le r_2} \sum\limits_{i=l}^ra_i \]

题解：

很明显是线段树维护区间最大子段和，立刻想到GSS1和GSS3，但GSS5很明显更难，难在回答询问。

如何维护区间最大子段和在GSS1和GSS3已有提及，这里就不再赘述，直接解决这题最核心的问题：如何回答询问。

询问的坑点就是左右区间可能重合，所以在询问时需分类讨论。

如果两个区间无交集：
如下图所示，蓝框中的元素必选，所以最大化区间\(\left[l_1,r_1 \right]\)和\(\left[l_2,r_2 \right]\)的选中部分的和。
即：取区间\(\left[l_1,r_1 \right]\)的最大后缀和与\(\left[l_2,r_2 \right]\)的最大前缀和。

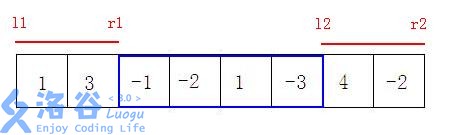
此部分代码：if(r1<l2) cout<<query(1,l1,r1).rs+query(1,r1,l2).sum+query(1,l2,r2).ls-a[l2]-a[r1]<<endl;

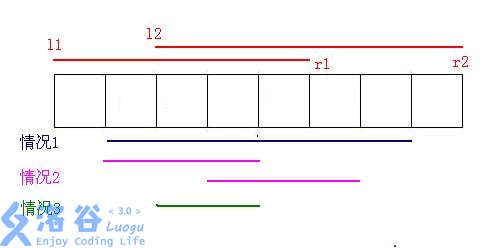
如果两个区间有交集：
如下图所示，分三种情况讨论：

1. 如果两个端点均在交叉的部分，此时的值是\(\max\limits_{r_1 \le l \le r \le l_2} \sum\limits_{i=l}^ra_i\)。
2. 如果其中一个端点在交叉的部分，此时的值是\(\max\limits_{l_1 \le l \le l_2,l_2 \le r \le r_1}\sum\limits_{i=l}^ra_i\)或\(\max\limits_{l_2 \le l \le r_1,r_1 \le r \le r_2}\sum\limits_{i=l}^ra_i\)。
3. 如果两个端点均不在交叉的部分，此时的值是\(\sum\limits_{i=l_2}^{r_1}a_i+\max\limits_{l_1 \le l \le l_2} \sum\limits_{i=l}^{l_2}a_i+\max\limits_{r_1 \le r \le r_2} \sum\limits_{i=r_1}^ra_i\)。
   
   此部分代码：

else{
    tree ans,a=query(lc,l,r),b=query(rc,l,r);
    ans.sum=a.sum+b.sum;ans.ps=max(a.ps,max(b.ps,a.rs+b.ls));
    ans.ls=max(a.ls,a.sum+b.ls);ans.rs=max(b.rs,b.sum+a.rs);
    return ans;
}

剩下的参考之前代码即可。
完整代码

总结

GSS1是后面的一个基础，是很简单的题。
GSS2就突然变得很离谱，虽然和GSS1很像但难度绝非同一档，甚至是GSS系列中的最难题。
GSS3相当于在GSS1的基础上加了单点修改，难度等于没有改变。
GSS4在Luogu有原题，不算难的题目，思维也不算难。
GSS5因为操作要分类讨论，所以较为麻烦，但总体思维难度还是比不上GSS2。
难度排序：GSS4 < GSS1|3 < GSS5 < GSS2

完结撒花