坐标转换:从图像坐标到世界坐标的旅程
本文来自公众号“AI大道理”。
——————
三维空间中的点如何一一对应到图像上?
图像上的点又如何反映射到三维空间的点上?
这就涉及世界坐标到像素坐标的转换。
1、坐标系
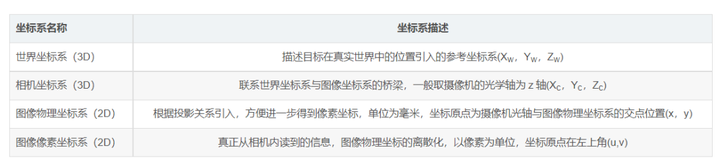
确定空间某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些坐标系之间的转换参数就是相机参数,求解参数的过程叫做相机标定。建立立体视觉系统所需要的各个坐标系,包括世界坐标系、相机坐标系、以及图像坐标系。
添加图片注释,不超过 140 字(可选)
添加图片注释,不超过 140 字(可选)
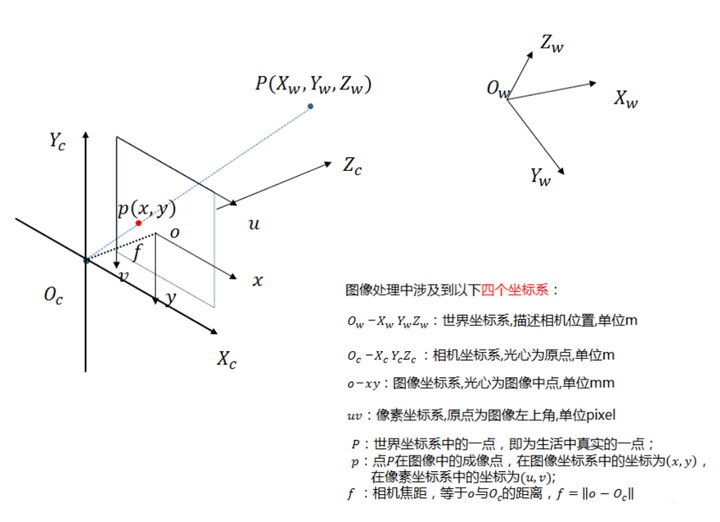
这张图就是世界中的点到相机图像上的点的转换关系图。转换过程涉及四个坐标系。相机坐标系,原点就是相机光心所在的位置。世界坐标系,真实世界中的三维点。图像坐标系,从世界点到图像点坐标的转换实际上是运用了相似三角形的计算。世界坐标点向像素坐标系点的转换,也就是我们所说的三维点向二维平面的投影。
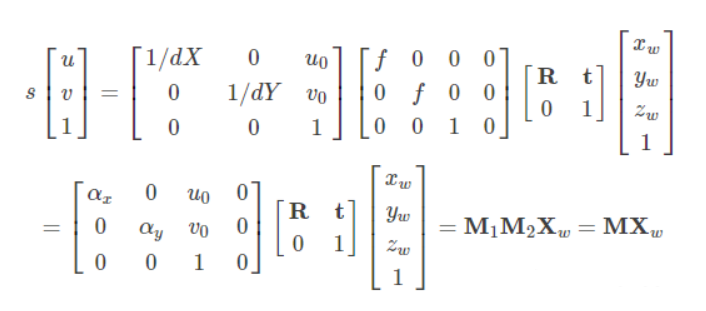
添加图片注释,不超过 140 字(可选)
添加图片注释,不超过 140 字(可选)
2、世界坐标->相机坐标->图像坐标->像素坐标
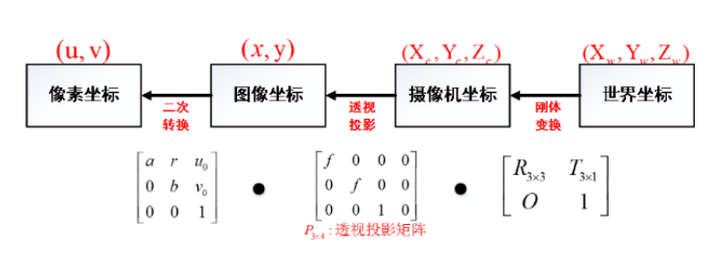
总过程:世界坐标->相机坐标->图像坐标->像素坐标。

添加图片注释,不超过 140 字(可选)
其中:f :摄像机的焦距,单位一般是mm;dx,dy :像元尺寸,即一个个像素的大小。u0,V0:图像中心。fx = f/dx, fy = f/dy :单位长度的像素个数,分别称为x轴和y轴上的归一化焦距。
(1)世界坐标->相机坐标
从真实世界到镜头,是一个刚性变换,意思就是仅发生了旋转和平移的变换。通过一个矩阵就可以描述旋转和平移变换。这个矩阵,就叫相机的外参矩阵。转换需要知道相机的外参,所谓外参就是相机相对于世界坐标系的相关关系,因此外参随着相机安装的高度、角度不断变化,一旦相机安装完毕,固定不动,外参也随之固定。摄像机的外参数有旋转向量R(3*3矩阵)和平移向量T(1*3矩阵)。
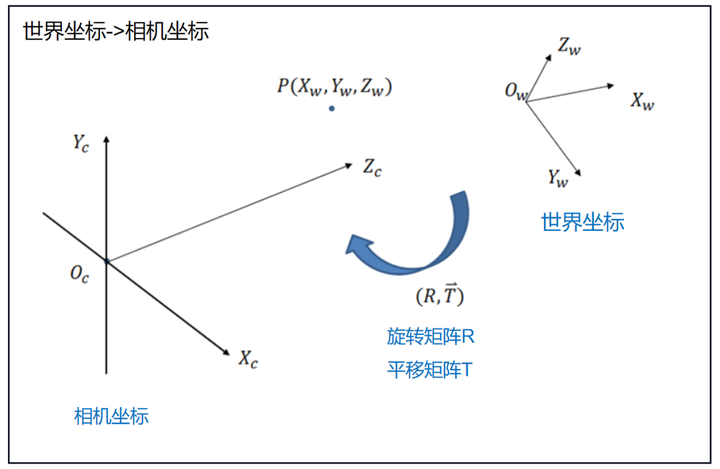
添加图片注释,不超过 140 字(可选)
转换公式:
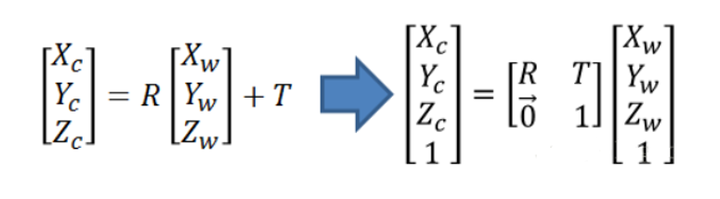
添加图片注释,不超过 140 字(可选)
(2)相机坐标->图像坐标
从镜头到图像坐标系,就是初中物理学的凸透镜成像的原理。理想情况下,用最简单的相似性就可以计算出来。然而实际情况是镜头会发生畸变,这个畸变就不能简单的用矩阵来描述了,需要一个非线性的函数。相机坐标是三维的,而图像是二维的,从三维转换为二维就是通过映射得到的。这是一个将三维的坐标系转化为二维的坐标系,这两个坐标系之间的转换要通过几何投影模型关系获得,下面是两个坐标系的投影关系示意图。
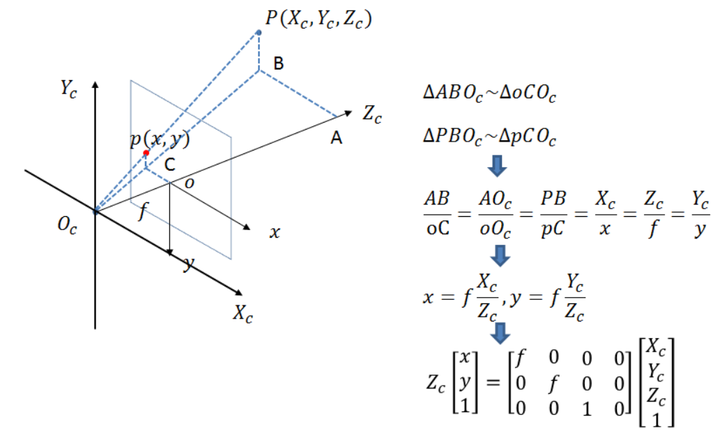
添加图片注释,不超过 140 字(可选)
通过三角形相似原理可进行转换。转换公式:
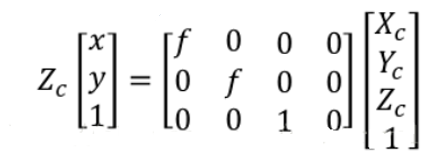
添加图片注释,不超过 140 字(可选)
f为焦距。
(3)图像坐标->像素坐标
从图像坐标系到像素坐标系,就是简单的平移、离散化。具体来讲是这样的,成像元件和镜头和中心是在同一水平线上的,原点(0,0)都是它们各自的正中心,成像元件的每一个感光单元实际上就是图像的一个像素。而对于像素坐标系,坐标(0,0)的是左上角的那个像素。物理坐标系是一个连续的概念,它是以毫米为单位,就好比某一观众在电影院里的具体坐标值(3.4,5.9);而像素坐标系是一个离散的概念,它是以像素作为单位,只能是整数值坐标,就好比某一观众在电影院里的位置是(第三排,第六列)。像素坐标系和图像坐标系都在成像平面上。以图像左上角为原点建立以像素(pixel)为单位的像素坐标系u-v。像素的横坐标u与纵坐标v分别是在其图像数组中所在的列数与所在行数,描述一个像素点都是几行几列。图像坐标系的原点为相机光轴与成像平面的交点O(u0,v0),通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm,属于物理单位。dx,dy表示每个像素在横轴x和纵轴y上的物理尺寸(单位为:mm/像素,单位像素的距离)。
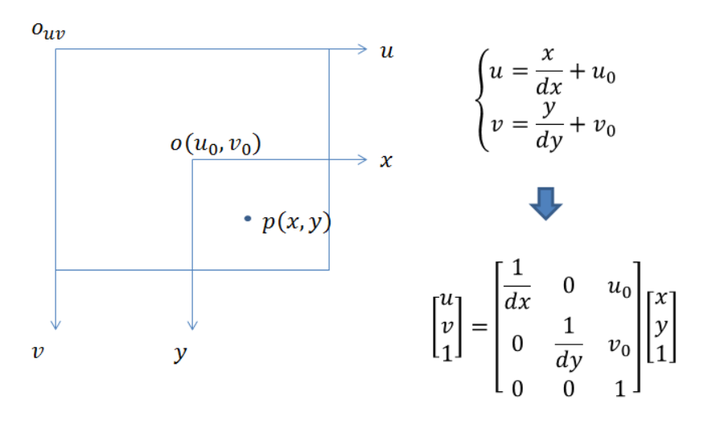
添加图片注释,不超过 140 字(可选)
转换公式:
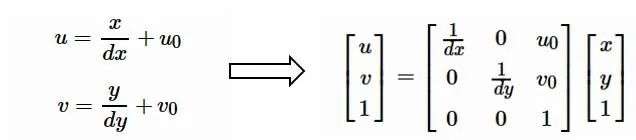
添加图片注释,不超过 140 字(可选)
例如:设CCD大小为8 x 6mm,拍摄的图像大小为640 x 480,则dx = 1/80(mm/像素)dy = 1/80(mm/像素), u0=320,v0=240。
总过程:世界坐标->相机坐标->图像坐标->像素坐标。

添加图片注释,不超过 140 字(可选)
3、像素坐标->图像坐标->相机坐标->世界坐标
二维图像坐标转化到三维世界坐标是不可能的,毕竟多出一个维度。
由于三维转二维的时候标定板就是直接设标定板到相机的距离为0,即z轴为0,因此,在二维图像坐标转化到三维世界坐标中我们也可以设置其中一个维度为已知的一个量,即Zc是可以求到的。在Zc已知的情况下才能进行像素到世界坐标的转换。由下转换公式也可证明这点。
总过程:像素坐标->图像坐标->相机坐标->世界坐标。
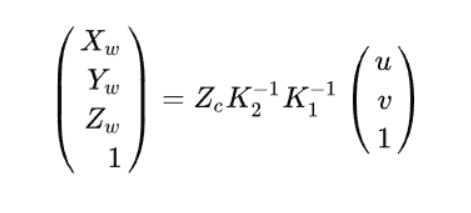
添加图片注释,不超过 140 字(可选)
(1)像素坐标->图像坐标
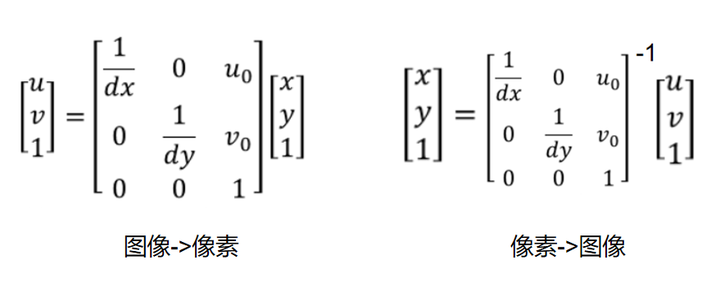
添加图片注释,不超过 140 字(可选)
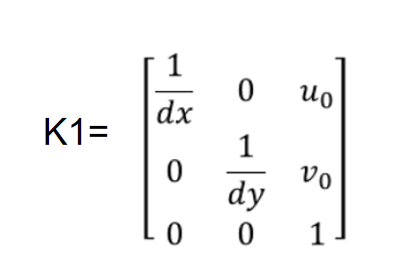
添加图片注释,不超过 140 字(可选)
(2)图像坐标->相机坐标
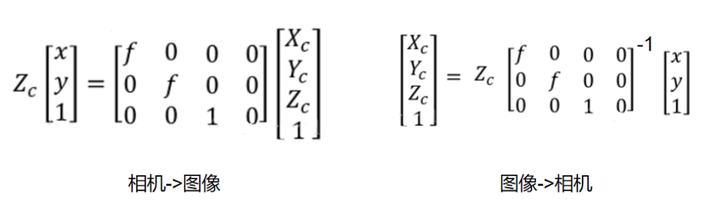
添加图片注释,不超过 140 字(可选)
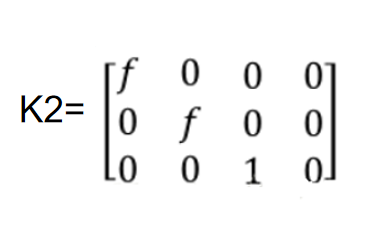
添加图片注释,不超过 140 字(可选)
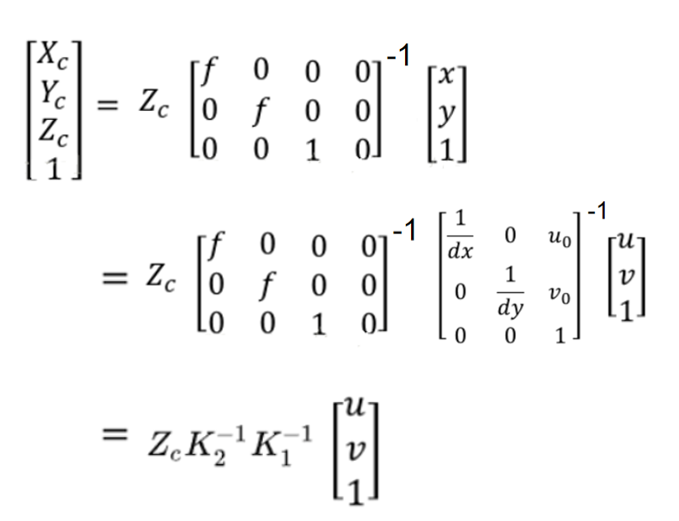
添加图片注释,不超过 140 字(可选)
(3)相机坐标->世界坐标
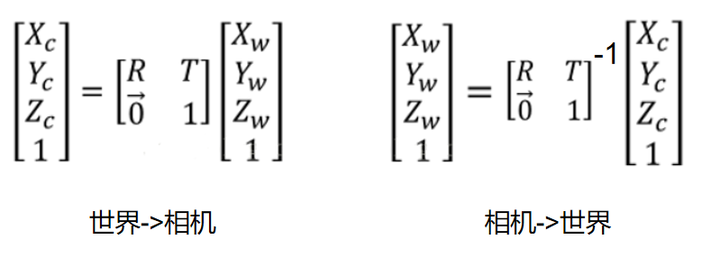
添加图片注释,不超过 140 字(可选)
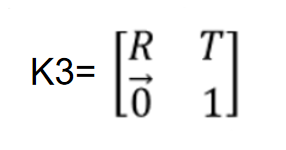
添加图片注释,不超过 140 字(可选)
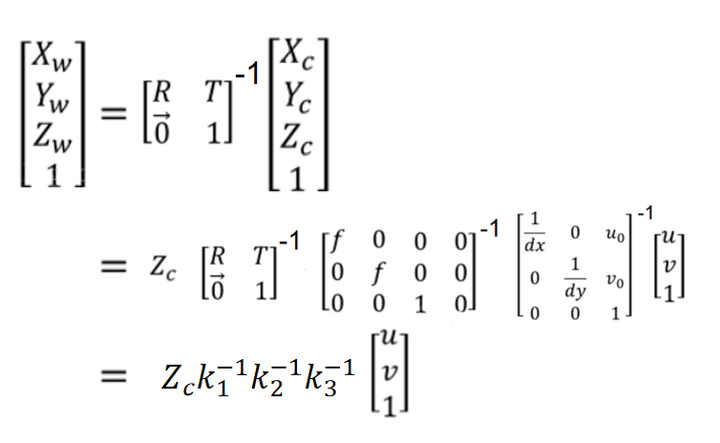
添加图片注释,不超过 140 字(可选)
(与总过程式子不一样是因为k代表的不一样)
4、坐标转换实验
取两个平移关系的相机分别拍摄一张图片,取图像上五个点位。
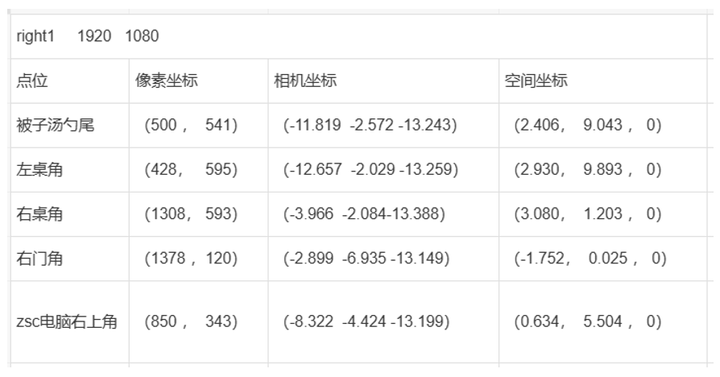
添加图片注释,不超过 140 字(可选)
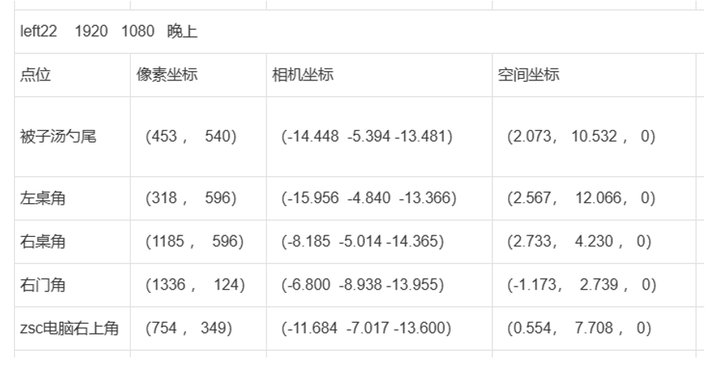
添加图片注释,不超过 140 字(可选)
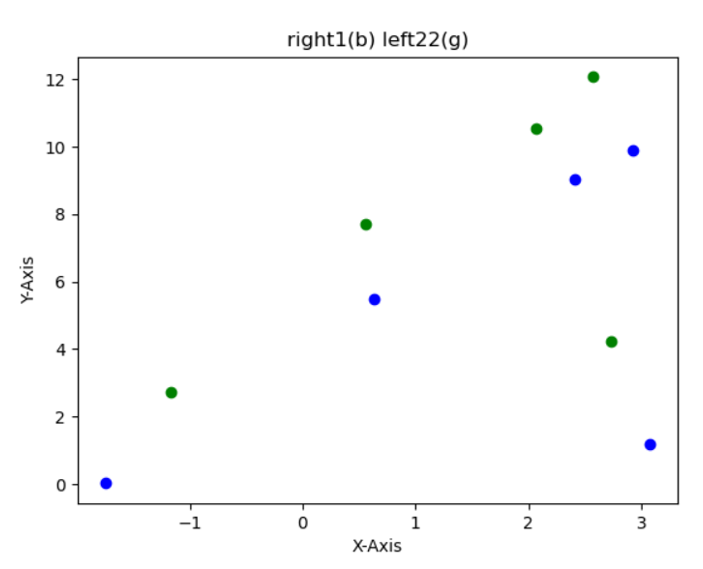
添加图片注释,不超过 140 字(可选)
5、总结
三维空间中的点一一对应到图像上是必然可行的,因为是在降维。
图像上的点映射到三维空间的点上是有条件的,需要先验一个维度,也就是说还是二维转二维的。
——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号—————————————————————

添加图片注释,不超过 140 字(可选)
—————————————————————
|
萍水相逢逢萍水,浮萍之水水浮萍!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号