AI大视觉（十) | Yolo v3中关于交叉熵与均方差损失函数的思考

​

本文来自公众号“AI大道理”

 

损失函数（误差函数）是关于模型输出和样本标签值之差的函数，通过对误差函数求导来调节权重参数。

本质：选取恰当的函数来衡量模型输出分布和样本标签分布之间的接近程度。

功能：调节权重参数

损失函数是网络学习的指挥棒，它引导着网络学习的方向——能让损失函数变小的参数就是好参数。

所以，损失函数的选择和设计要能表达你希望模型具有的性质与倾向。

 

 

​交叉熵损失函数

交叉熵是用来衡量两个概率分布的距离。

 

 

​

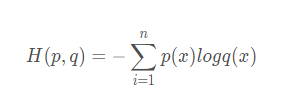
使用交叉熵的背景：

 

 

​

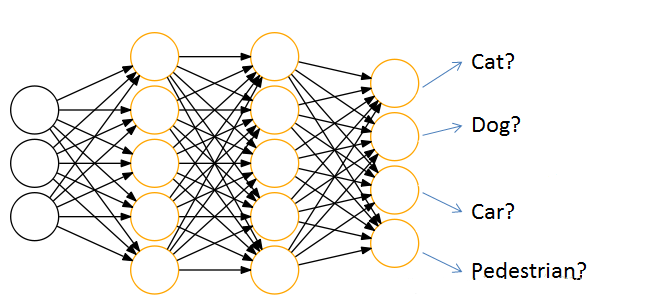
通过神经网络解决分类问题时，一般会设置k个输出点，k代表类别的个数，

每个输出结点，都会输出该结点对应类别的得分，如[cat，dog，car，pedestrian] 为[44，10，22，5]。

但是输出结点输出的是得分，而不是概率分布，那么就没有办法用交叉熵来衡量预测结果和真确结果了，那怎么办呢。

解决方法是在输出结果后接一层 softmax，softmax的作用就是把输出得分换算为概率分布。

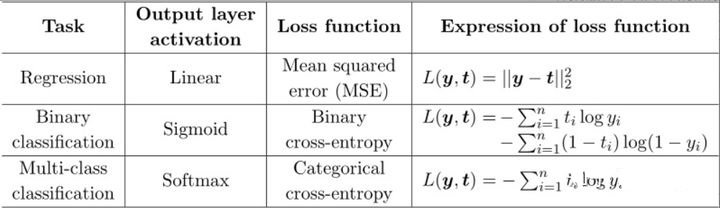
交叉熵+sigmoid 输出为单值输出，可用于二分类。

交叉熵+softmax 输出为多值，可用于多分类。

 

为什么使用交叉熵作分类，而不用作回归？

可以替代均方差+sigmoid组合解决梯度消失问题，另外交叉熵只看重正确分类的结果，而均方差对每个输出结果都看重。

 

 

 

​均方差损失函数

均方差是预测值与真实值之差的平方和，再除以样本量。 均方差函数常用于线性回归，即函数拟合。

 

 

​

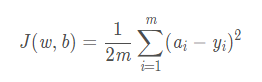
回归问题与分类问题不同，分类问题是判断一个物体在固定的n个类别中是哪一类。

回归问题是对具体数值的预测。

比如房价预测，销量预测等都是回归问题，这些问题需要预测的不是一个事先定义好的类别，而是一个任意实数。

在训练时，如果预测值与实际值的误差越大，那么在反向传播训练的过程中，各种参数调整的幅度就要更大，从而使训练更快收敛。

 

均方差为什么不适用于分类问题，而适用于回归？

因为经过sigmoid函数后容易造成梯度消失，所以不适用于分类问题。

均方差适用于线性的输出，特点是与真实结果差别越大，则惩罚力度越大。

 

 

​区别

在一个三分类模型中，模型的输出结果为（a,b,c)，而真实的输出结果为(1,0,0)，那么MSE与cross-entropy相对应的损失函数的值如下：

 

 

 

​

 

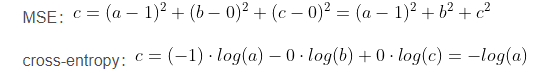
交叉熵的损失函数只和分类正确的预测结果有关系，而MSE的损失函数还和错误的分类有关系。

均方差分类函数除了让正确的分类尽量变大，还会让错误的分类变得平均。

实际在分类问题中这个调整是没有必要的，错误的分类不必处理。

但是对于回归问题来说，这样的考虑就显得很重要了，回归的目标是输出预测值，而如果预测值有偏差，是一定要进行调整的。

所以，回归问题使用交叉熵并不合适。

 

 

 

​

 

 

​yolo v3中的损失函数

 

YOLOv3将分类预测改为回归预测，分类损失函数换成了二值交叉熵损失函数。

Loss 要计算：

• 中心点的 Loss
• 宽高的 Loss
• 置信度的 Loss
• 目标类别的 Loss

 

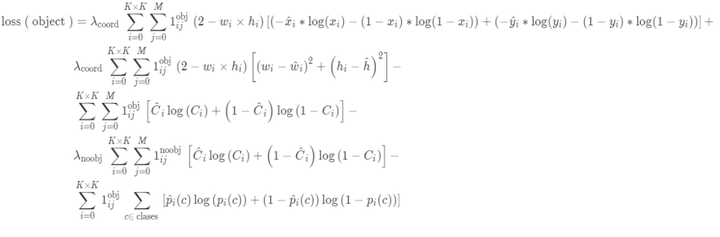
其中：

宽高w、h的loss使用均方差损失函数。

中心点的坐标x、y的loss、置信度c的loss和目标类别p的loss使用交叉熵损失函数。

 

 

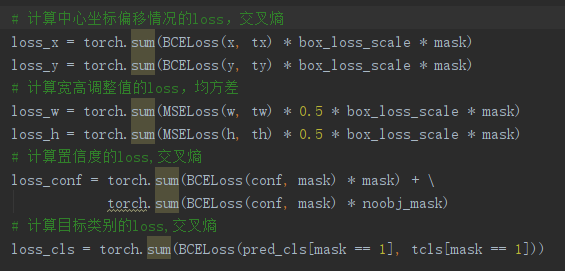
解释：

对于目标类别obj 的loss，Logistic回归正好方差损失和交叉熵损失的求导形式是一样的，都是output - label的形式。

本这里应该用（二元分类的）交叉熵损失函数的，但在代码里也可直接用均方差损失函数代替。

 

​

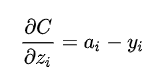
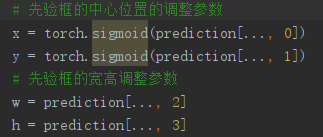
对于中心点的坐标x、y的 loss，DarkNet官方代码实现的YOLOV3里面坐标损失用的是交叉熵BCE Loss，而YOLOV3官方论文里面说的是均方差MSE Loss。

对于宽高w、h的loss是均方差MSE Loss，因为没有经过sigmoid，而x、y是交叉熵BCE Loss因为经过了sigmoid。

 

 

 

 

​总结

 

yolov3中论文的损失函数与实际代码实现用的损失函数有些许不同，但不影响最终效果。

 

 

 

​

 

 

——————

浅谈则止，细致入微AI大道理

扫描下方“AI大道理”，选择“关注”公众号

—————————————————————

 

 

​

 

​

—————————————————————

投稿吧 | 留言吧

 

 

​