（数学）P、NP、NPC、NP hard问题

概念定义：

 

http://m.elecfans.com/article/757041.html

https://www.cnblogs.com/AndyJee/p/5048556.html

P问题：能在多项式时间内解决的问题；

NP问题：（Nondeterministic Polynomial time Problem）不能在多项式时间内解决或不确定能不能在多项式时间内解决，但能在多项式时间内验证的问题；

NPC问题：（NP Complete）NP完全问题，所有NP问题在多项式时间内都能规约（Reducibility）到它的NP问题，即解决了此NPC问题，所有NP问题也都能得到解决；

NP hard问题：NP难问题，所有NP问题在多项式时间内都能规约（Reducibility）到它的问题，但不一定是NP问题。

概念图解：

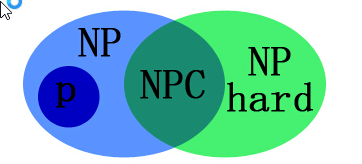
说明：

1. P问题属于NP问题，NPC问题属于NP问题；
2. NPC问题同时属于NP hard问题，是NP与NP hard问题的集合。

概念应用：

NPC问题有很多的，比较有名的有团问题，顶点覆盖集问题，支配集问题，独立集问题，哈密顿路问题，旅行商问题等，同样有很多是NP-hard而不是NPC的问题，比如围棋，停机问题等。

P、NP与NPC 的通俗理解

1.多项式时间复杂度

定义： 解决问题需要的时间与问题的规模之间是多项式关系。

多项式关系形如，k为某个常数，n是问题的输入规模。例如，时间复杂度为O(nlog(n))、O(n^3)都是多项式时间复杂度。时间复杂度为O(n^log(n))、O(2^n)是指数时间复杂度，O(n!)是阶乘时间复杂度。像O(a^n)和O(n!)型的时间复杂度，它是非多项式级的，其复杂度计算机往往不能承受。

为什么多项式时间复杂度的定义形式是呢，它的多项式的多项性体现在哪呢？

因为算法的时间复杂度的表达式，取指数最高项保留作为时间复杂度的表达式，未删除低指数项就可以看出多项式的多项性了吧！当然，单项式也算作多项式。

注：图G的顶点个数称为图G的阶(Order)。

2.P问题

《算法导论》给出的定义：在多项式时间内可解的问题为P问题（Polynomial Problem，多项式问题）。

更为具体的是：P问题指可以在多项式时间内求解的问题，例如：时间复杂度为O(nlog(n))的快速排序和堆排序，的算法是指数时间算法。

3.NP问题

定义： NP问题（(Non-deterministic Polynomial Problem，非确定性多项式问题），指问题只能通过验证给定的猜测是否正确来求解。所谓多项式指的是验证猜测可在多项式时间内完成，所谓非确定性指的是问题只能通过验证猜测来解，而不能直接求解。

如Hamilton回路是NP问题，因为验证一条路是否恰好经过了每一个顶点可在多项式时间内完成，但是找出一个Hamilton回路却要穷举所有可能性，不能直接求解。

又如大合数的质因数分解，没有给定的公式可直接求出一个合数的两个质因数是什么，但是验证两个数是否是质因数却可在多项式时间完成，所以它也是非确定性多项式问题，即NP问题。

之所以要定义NP问题，是因为通常只有NP问题才可能找到多项式的算法。我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。

简单的说，存在多项式时间的算法的一类问题，称之为P类问题；而像梵塔问题，推销员旅行问题等问题，至今没有找到多项式时间算法解的一类问题，称之为NP问题。同时，P类问题是NP问题的一个子集。也就是说，能多项式时间地解决一个问题，必然能多项式时间地验证一个问题的解。

3.1NP与P的关系

目前，人类还未解决的问题是：是否所有的NP问题都是P类问题，即P=NP?。这就是注明的世界七大数学难题之首。虽然这个问题尚未解决，但是，一个总的趋势和大方向是人们普遍认为，P=NP不成立，也就是说，多数人相信，存在至少一个不可能有多项式级复杂度的算法的NP问题。

人们如此坚信P≠NP是有原因的，就是在研究NP问题的过程中找出了一类非常特殊的NP问题叫做NP-完全问题（Non-deterministic Polynomial Complete Problem），也即所谓的 NPC问题。正是NPC问题的存在，使人们相信P≠NP。

4.NPC问题

4.1约化

为了说明NPC问题，我们先引入一个概念——约化(Reducibility，有的资料上叫“归约”（Reduction）) 。

约化的概念： 
约化的标准概念：如果能找到这样一个变化法则，对任意一个程序A的输入，都能按这个法则变换成程序B的输入，使两程序的输出相同，那么我们说，问题A可约化为问题B，即可以用问题B的解法解决问题A，或者说，问题A可以“变成”问题B。 如：一元一次方程可以“归约”为一元二次方程。

约化的性质： 
约化具有一项重要的性质：约化具有传递性。如果问题A可约化为问题B，问题B可约化为问题C，则问题A一定可约化为问题C。

约化的意义： 
问题A可约化为问题B”有一个重要的直观意义：B的时间复杂度高于或者等于A的时间复杂度。也就是说，问题A不比问题B难。

约化的要求： 
我们所说的“可约化”指的是可“多项式时间地”约化(Polynomial-time Reducible)，即变换输入的方法是能在多项式的时间里完成的。约化的过程只有用多项式的时间完成才有意义。

4.2NPC问题

NPC问题是指满足下面两个条件的问题： 
（1）它是一个NP问题； 
（2）所有的NP问题都可以用多项式时间约化到它。

所以显然NP完全问题具有如下性质：它可以在多项式时间内求解，当且仅当所有的其他的NP完全问题也可以在多项式时间内求解。这样一来,只要我们找到一个NPC问题的多项式解，所有的NP问题都可以多项式时间内约化成这个NPC问题，再用多项式时间解决，这样NP就等于P了。

目前，NPC问题还没有找到一个多项式时间算法，因此我们就此可直观地理解，NPC问题目前没有多项式时间复杂度的有效算法，只能用指数级甚至阶乘级复杂度的搜索。

大多数人的观点对于 P类问题，NP类问题，NPC之间的关系可用下图表示（此图正确性有待验证）：

4.3第一个NPC问题

逻辑电路问题是第一个NPC问题。逻辑电路问题指的是这样一个问题：给定一个逻辑电路，问是否存在一种输入使输出为True。

逻辑电路问题属于NPC问题。这是有严格证明的。它显然属于NP问题，并且可以直接证明所有的NP问题都可以约化到它（不要以为NP问题有无穷多个将给证明造成不可逾越的困难）。证明过程相当复杂，其大概意思是说任意一个NP问题的输入和输出都可以转换成逻辑电路的输入和输出（想想计算机内部也不过是一些0和1的运算），因此对于一个NP问题来说，问题转化成了求出满足结果为True的一个输入（即一个可行解）。

有了第一个NPC问题后，一大堆NPC问题就出现了，因为再证明一个新的NPC问题只需要将一个已知的NPC问题约化到它就行了。后来，Hamilton回路成了NPC问题，TSP问题（旅行商问题）也成了NPC问题。现在被证明是NPC问题的还有很多，任何一个NPC问题找到了多项式算法的话所有的NP问题都可以完美解决了。因此说，正是因为NPC问题的存在，P=NP变得难以置信。P=NP问题还有许多有趣的东西，有待大家自己进一步的挖掘。攀登这个信息学的巅峰是我们这一代的终极目标。现在我们需要做的，至少是不要把概念弄混淆了。

5.NPH问题

NPH问题（NP难问题，英文NP-hard问题），其满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 NPC问题的范围广，但不一定是NP问题）。

NP-Hard问题同样难以找到多项式时间复杂度的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。

在《嫌疑人X的献身》中，石神和汤川讨论，解决一个命题和判断一个命题是否正确，哪个更难。讨论中，他们提到了P≠ NP的证明。这是一个困扰了不仅仅是计算机科学家，也包括数学家、经济学家、甚至哲学家以久的问题。同时，P/NP是7个千禧年数学难题之一，足见其重要性和难度之大。

....

不过，P与NP这个命题为何如此重要？P与NP分别是什么含义？我们普通小白到底能弄懂吗？

《可能与不可能的边界：P/NP问题趣史》就尝试用科普的笔法来讲述P/NP历史、渊源和含义。不过，菲菲认为，要完全理解这本书，还是需要一点点计算机思维、人工智能算法常识，甚至一点点数学基础的。否则，可能会出现，能理解作者说的每一个字、看得懂每一段话，却不懂背后逻辑关系的“尴尬局面”（回忆一下英语阅读考试的感受...）。

可能与不可能的边界

说到这里，大家是不是对P/NP有些恐惧了？其实，这个问题远没有它看上去那么复杂，忽略其背后的数学和计算机科学定义之后，这个问题最终可以简化为：

这个世界到底有没有捷径？

有捷径？没有捷径？

先来解释一下这个拗口的P和NP是什么意思。注意，菲菲的解释是极端极端简化的，是刻意忽略了背后的数学严谨性，让每个人都能感性上理解这个命题：

P代表了这样一类问题，计算机在解决它们的时候可以有速度非常快的方法。这个速度和计算机硬件无关，仅仅取决于这个解决方法本身的便捷性。

NP代表了另一类问题，它们有最优解，但是，其中很多问题，计算机在寻求最优解时，没有快速的方法，甚至，只能傻傻的、暴力的、尝试所有可能的组合，然后找到最优解。NP问题中，最难的一类问题，被称为NPC，也就是NP完全问题。

好了，理解了P和NP的定义后，下面就是科学家想要寻找的真理了：

如果P=NP，则意味着，每一个NP问题都可以转化成P，也就是每一个难题最终可以变成一个简单命题，让计算机可以快速求解。

如果P≠NP，则意味着，很多NP问题无法简化成P, 也就是计算机只能很傻很暴力的去求解。

换而言之，就是，人类在解决复杂问题的时候是否有捷径？

说到这里，大家可能还没有意识到如果P=NP的威力。下面，就来给大家展示一下如果人类找到了世界的捷径，也就是找到了P=NP的方法后，世界会成为一个怎样神奇的样子！

充满捷径的神奇世界

大家熟知的证券市场，充满了各种信息，它们交互作用，让准确的结果预测变得完全不可能。这是一个典型的混沌系统，如同天气系统、海洋、足球力学系统一样。然而，如果P=NP，计算机一下子变得足够聪明，当获知了所有信息因子后，计算机竟然可以在极其短时间里，作出极其准确的预测了！从今往后，人们将可以准确预测天气、股票、球赛结果...

大家是不是已经在惧怕人工智能了？是不是已经在担心机器人将统治我们？但是，比起P=NP 的神奇世界，现在的人工智能还是很蠢的。如果P=NP，机器人将比现在聪明更多更多更多。从此以后，人工智能将可以快速的自我优化了！那时候，人类的末日可能真的就来了。

当P=NP，计算机将很容易找到一个算法，来知道艺术作品是如何直击人类心灵的，于是，计算机能为每个人订制出他最喜爱的音乐、艺术作品。什么，你认为现在的音乐推荐系统已经可以做到？不不不，在那个P=NP的时代，计算机会自我将算法进化到，钻进你的内心，成为你的私人订制作曲家。

如今，人类虽然掌握有人类基因数据库的数据，但是对其进行数据分析依然是个NP完全问题，这让科学家即便花费极大运算力气能找出致病基因，也难以个体化订制药品。然而，如果计算机科学家们能够解开P=NP，从此以后，计算机将能快速为每一位患者订制出药物，不管是癌症还是其他和基因有关的疾病。而且为你订制的药物，将不会对你产生副作用，而别人使用未必有用。这世间，再无绝症。

P=NP真的可能吗？

人类至今还没有找到让任何NP问题变成P问题的算法。虽然一些NP问题数学家或者计算机科学家们找到了一些比较快速并且准确率较高的算法，但是，一个能放之四海而皆准的算法依然没有被找到。

那没有被找到是不是就不存在呢？

如今，绝大部分计算机科学家认为，P≠NP, 也就是，那个能轻易解开世界所有谜题的解并不存在。

同样，人们从直觉、哲学和宗教来看，也难以相信，有解开世界上所有问题的一把简单钥匙。因为，如果这样的钥匙真的存在，它大概早已在这个宇宙中存在了。比如，人类可能早已有了万事万物看一遍就会的本领，或是某种生物一生下来就不必为了生存而抗争，因为它们的算法极其优异，可以在任何环境中以最高效的方式生存下来。

然而，既然人们直觉上相信，这样的宇宙捷径并不存在，但是证明其不存在，可不是一件简单的事情。

证明P≠NP

任何一个能够证明P≠NP的人，都可以得到百万美金的奖励。这么多年过去，无数的数学家和计算机科学家都努力过，每年都有数以万计的论文寄往委员会，至今，却没有人获得这笔奖金。

终其原因，正是本文开头提到的石神和汤川的讨论：提出一个猜想（也就是出题）很容易，但要判断其答案是否正确，非常难。人们猜想了P≠NP，却非常难以证明。

很多人不理解数学家为什么会非要“证明”一个猜想。“证明”一个猜想，有非常重要的意义，比如，在P≠NP这个问题上，一旦能够证明，就意味着，人们不必再花心血去寻找那个超级算法了，因为，逻辑上，它根本不可能存在！

只是，至今为止，很多试图证明P≠NP的过程都是错误的，人们最常犯的一个错误是，他们提出一些可能让P=NP成立的算法，然后证明这些算法并不可能存在，进而得出P≠NP的结论。然而，这个逻辑最大的错误在于：这些提出的可能的算法不成立，不带表别的算法不成立。其实，在日常生活中，人们也很容易犯这样的逻辑错误：自己做不到，不等于别人做不到，但人们依然经常认为自己做不到的事情别人也做不到。

那么，人们最终可以证明P≠NP吗？

菲菲最近在一个相关论坛看到一段很有趣的评论：每当有P≠NP的证明出来，委员会都需要用NP的时间来判断这个证明是否正确。也许，要猜想P≠NP是否能被证明，本身就是个NP问题。

不过，鉴于困扰人类几百年的费马大定理最终终于被证明了，我们依然应当对P≠NP的证明抱有希望。

另外，说不定，某天真的找到了P=NP的算法？只是，不知这到底是喜是悲呢？人们如今已经在怀念那个没有那么多数据和信息的“慢生活”时代，等宇宙捷径真的被发现了，生命和生活还能如现在这样，充满了悬念、残缺之美吗？