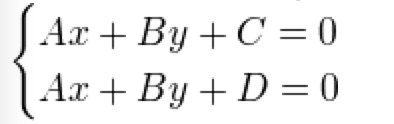齐次坐标
齐次性的定义和齐次坐标系的定义: https://www.cnblogs.com/xin-lover/p/9486341.html
齐次坐标无穷远点表示及齐次性的理解: https://blog.csdn.net/janestar/article/details/44244849
齐次坐标变换: https://blog.csdn.net/zx3517288/article/details/79154036
https://zhuanlan.zhihu.com/p/258437902
齐次坐标优势: https://zhuanlan.zhihu.com/p/46292266
齐次坐标下点和向量的表示: https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
1 问题引出:两条平行线可以相交于一点
在欧氏几何空间,同一平面的两条平行线不能相交,这是我们都熟悉的一种场景。
然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。
欧氏空间(或者笛卡尔空间)描述2D/3D几何非常适合,但是这种方法却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),2维笛卡尔坐标可以表示为(x,y)。
如果一个点在无穷远处,这个点的坐标将会(∞,∞),在欧氏空间,这变得没有意义。平行线在透视空间的无穷远处交于一点,但是在欧氏空间却不能,数学家发现了一种方式来解决这个问题。
2 什么是齐次坐标?
简而言之,齐次坐标就是用N+1维来代表N维坐标
我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标,因此,一个点(X,Y)在齐次坐标里面变成了(x,y,w),并且有
X = x/w
Y = y/w
例如,笛卡尔坐标系下(1,2)的齐次坐标可以表示为(1,2,1),如果点(1,2)移动到无限远处,在笛卡尔坐标下它变为(∞,∞),然后它的齐次坐标表示为(1,2,0),因为(1/0, 2/0) = (∞,∞),我们可以不用”∞"来表示一个无穷远处的点了,哈哈。
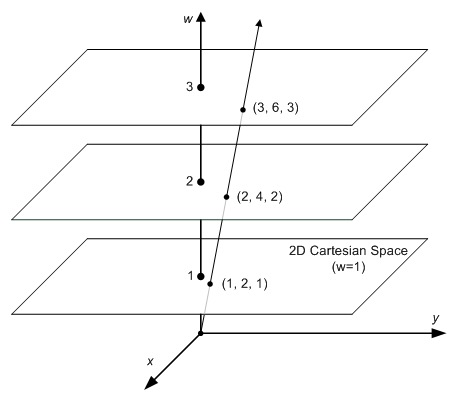
3 齐次的含义
我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。
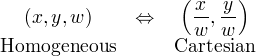
转化齐次坐标到笛卡尔坐标的过程中,我们有一个发现,例如:

你会发现(1, 2, 3), (2, 4, 6) 和(4, 8, 12)对应同一个Euclidean point (1/3, 2/3),任何标量的乘积,例如(1a, 2a, 3a) 对应 笛卡尔空间里面的(1/3, 2/3) 。因此,这些点是“齐次的”,因为他们代表了笛卡尔坐标系里面的同一个点。换句话说,齐次坐标有规模不变性。
证明:两条直线可以相交
考虑如下方程组:
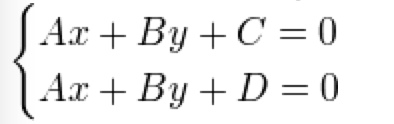
我们知道在笛卡尔坐标系里面,该方程组无解,因为C ≠ D,如果C=D,两条直线就相同了。
让我们在透视空间里面,用齐次坐标x/w, y/w代替x ,y,
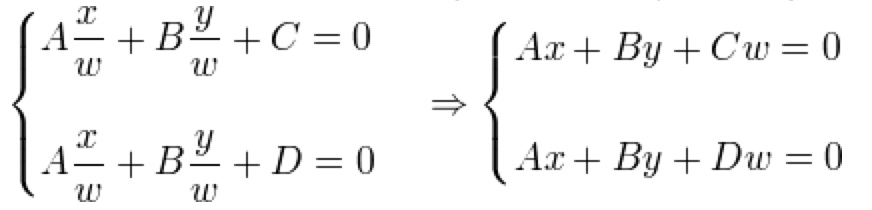
现在我们有一个解(x, y, 0),两条直线相交于(x, y, 0),这个点在无穷远处。
4 为什么需要齐次坐标
最主要的目的是方便计算机图形学进行仿射几何变换。简单的理解就是可以使用矩阵同时描述旋转和平移,这样我们就可以使用矩阵相乘来表述物体的旋转、缩放和平移了
齐次坐标的使用能够大大简化在三维空间中的点线面表达方式和旋转平移等操作,具体分如下几点进行说明。
1、能否非常方便的表达点在直线或平面上
在2D平面上,一条直线 l 可以用方程 ax + by + c = 0 来表示,该直线用向量表示的话一般记做
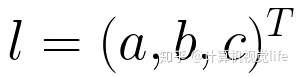
我们知道点p = (x, y)在直线 l 上的充分必要条件是 ax + by + c = 0
如果使用齐次坐标的话,点p的齐次坐标就是
p'=(x, y, 1)
那么 ax + by + c = 0 就可以用两个向量的内积(点乘)来表示:
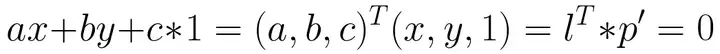
因此,点p在直线l上的充分必要条件就是 直线l 与p的齐次坐标p'的内积:
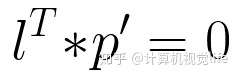
是不是很方便呢!
同理,我们知道 三维空间的一个平面A可以用方程 ax + by + cz + d = 0 来表示,三维空间的一个点P=(x, y, z) 的齐次坐标 P'=(x, y, z, 1),类似的,点P在空间平面A上可以用两个向量的内积来表示,如下:
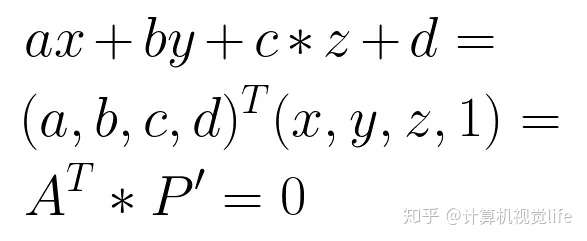
因此,点P在平面A上的充分必要条件就是平面A 向量与P的齐次坐标P'的内积(点乘):
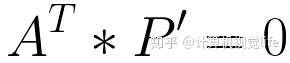
2、方便表达直线与直线,平面与平面的交点
先给出结论,后面再具体解释:
结论:在齐次坐标下,可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l,也就是
l = p x q
也可以使用两条直线 l, m 的叉乘表示他们的交点 x
x = l x m
见下面示例图。
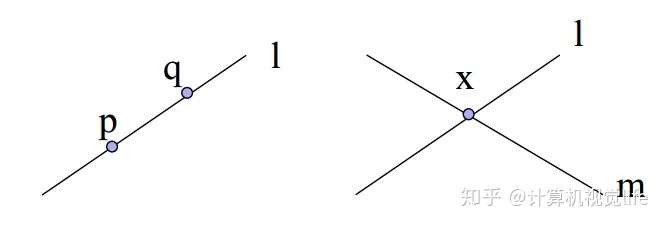
之所以可以这么简洁的表示交点是因为采用了齐次坐标的表示方式。
那么这是为什么呢?
先介绍一下叉乘(也称叉积、外积)的概念:
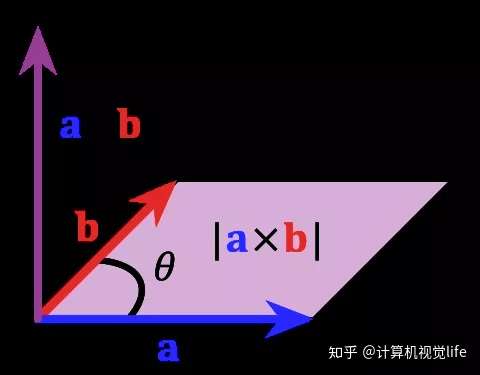
两个向量 a和b 的叉乘仅在三维空间中有定义,写作 a x b
a x b 是与向量 a, b都垂直的向量,其方向通过右手定则(见下图)决定。
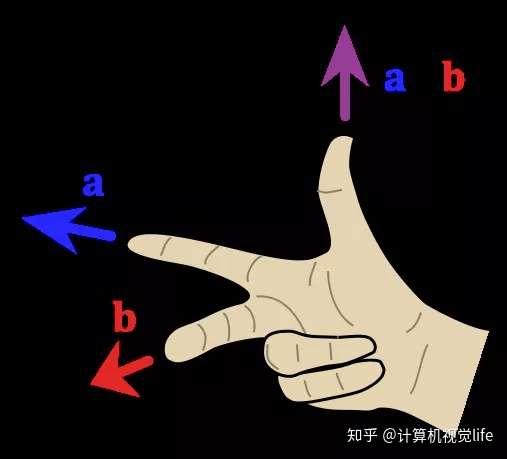
其模长等于以两个向量为边的平行四边形的面积(见下图)。
叉乘可以定义为:

其中 θ表示a, b的夹角(0°到180°之间),||a||, ||b||是向量a, b的模长
n则是一个与向量a, b所构成的平面垂直的单位向量
根据叉乘定义:
向量自身叉乘结果为0,因为夹角为0。也就是说三维向量 a x a =0, b x b = 0而点乘(也称点积,内积)的定义是
a * b = ||a||* ||b|| *cos(θ)
根据定义:如果两个向量垂直,cos(θ) = 0,点积也为0。
好了,经过上面点乘和叉乘定义的铺垫。下面来推导一下上面的结论:
为什么两条直线 l, m 的叉乘 l x m 等于它们的交点 p,也就是 p = l x m?
原因如下:首先,根据前面叉乘的定义,l x m 的结果向量(记为 p = l x m) 与 l 和 m都垂直,根据点乘的定义,垂直的向量之间的点积为0,因此可以得到:
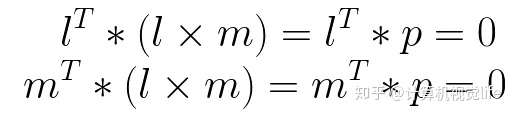
因此,根据前面点在直线上的结论,可以看到p既在直线l 上又在直线m上,所以 p = l x m 是两条直线的交点。此处 p 是齐次坐标。
同样的,可以证明,两点p, q 的叉乘 可以表示 过两点的直线l,即 l = p x q。(留做作业)
3、能够区分一个向量和一个点
先给出结论:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR。
由于作者对齐次坐标真的解释的不错,我就原封不动的摘抄过来:
对于一个向量 v 以及基oabc,可以找到一组坐标(v1,v2,v3),使得v = v1 a + v2 b + v3 c (1)
而对于一个点 p,则可以找到一组坐标(p1,p2,p3),使得 p – o = p1 a + p2 b + p3 c (2),
从上面对向量和点的表达,我们可以看出为了在坐标系中表示一个点(如p),我们把点的位置看作是对这个基的原点o所进行的一个位移,即一个向量——p – o(有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量),我们在表达这个向量的同时用等价的方式表达出了点p:p = o + p1 a + p2 b + p3 c (3)
(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7),谁知道它是个向量还是个点!
我们现在把(1)(3)写成矩阵的形式:v = (v1 v2 v3 0) X (a b c o)
p = (p1 p2 p3 1) X (a b c o),这里(a,b,c,o)是坐标基矩阵,右边的列向量分别是向量v和点p在基下的坐标。这样,向量和点在同一个基下就有了不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
这样,上面的(1, 4, 7)如果写成(1,4,7,0),它就是个向量;如果是(1,4,7,1),它就是个点。下面是如何在普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知,对于平移T、旋转R、缩放S这3个最常见的仿射变换,平移变换只对于点才有意义,因为普通向量没有位置概念,只有大小和方向.
而旋转和缩放对于向量和点都有意义,你可以用类似上面齐次表示来检测。从中可以看出,齐次坐标用于仿射变换非常方便。
此外,对于一个普通坐标的点P=(Px, Py, Pz),有对应的一族齐次坐标(wPx, wPy, wPz, w),其中w不等于零。比如,P(1, 4, 7)的齐次坐标有(1, 4, 7, 1)、(2, 8, 14, 2)、(-0.1, -0.4, -0.7, -0.1)等等。因此,如果把一个点从普通坐标变成齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;如果把一个齐次坐标转换成普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。
由于齐次坐标使用了4个分量来表达3D概念,使得平移变换可以使用矩阵进行,从而如F.S. Hill, JR所说,仿射(线性)变换的进行更加方便。由于图形硬件已经普遍地支持齐次坐标与矩阵乘法,因此更加促进了齐次坐标使用,使得它似乎成为图形学中的一个标准。
以上很好的阐释了齐次坐标的作用及运用齐次坐标的好处。其实在图形学的理论中,很多已经被封装的好的API也是很有研究的,要想成为一名专业的计算机图形学的学习者,除了知其然必须还得知其所以然。这样在遇到问题的时候才能迅速定位问题的根源,从而解决问题。
4、能够表达无穷远
比如 两条平行的直线 ax+by+c=0, ax+by+d=0,
可以分别用向量 l = (a, b, c), m = (a, b,d)表示
根据前面直线交点的计算方法,其交点为 l x m
根据叉乘计算法则
向量
的叉乘结果可以用如下方法计算得到
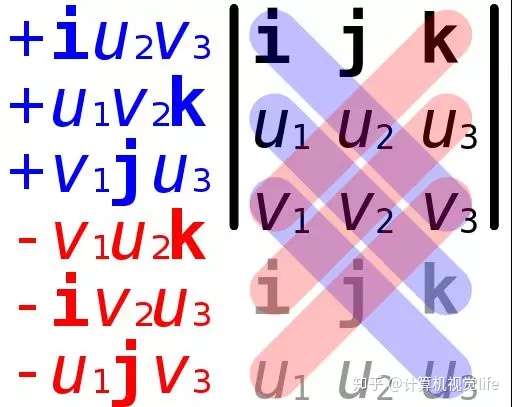
最终:l x m = (d-c)(b,-a,0),忽略标量(d-c),我们得到交点为(b,-a,0),并且是齐次坐标,如果要转化为非齐次坐标,那么会得到 (b/0, a/0),坐标是无穷大,可以认为该点为无穷远点,这与我们通常理解的:平行线相交于无穷远的概念相吻合。
因此,如果一个点的齐次坐标中,最后一个元素为0,则表示为无穷远点。
5、更简洁的表达欧氏空间变换
这是齐次坐标最重要的一个优势之一。在以后的学习中你会更加深刻的理解。
使用齐次坐标,可以方便的将加法转化为乘法,方便的表达平移。
比如我们要完成将2D坐标点x=[u,v]' 平移t=[tu, tv],如果用非齐次方法的话,是用如下的加法
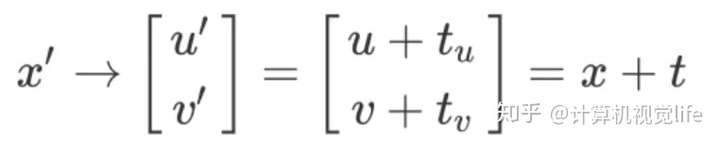
如果用齐次坐标表示时可以将加法转换为乘法
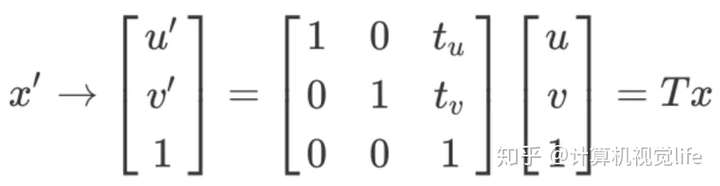
在欧氏变换中一般有两种操作:旋转和平移。
如果我们想要将向量a进行一个标准的欧氏变换,一般是先用旋转矩阵R进行旋转,然后再用向量t进行平移,其结果a' = R*a + t,这样看起来没什么问题。
但是,我们知道SLAM中一般都是连续的欧氏变换,所以会有多次连续的旋转和平移,假设我们将向量a进行了两次欧氏变换,分别为R1, t1 和 R2,t2,分别得到:
b = R1*a + t1, c = R2*b + t2
最终的结果 c = R2*(R1*a + t1) + t2
显然,这样的变换在经过多次后会变的越来越复杂。其根本原因是上述表达方式并不是一个线性的变换关系。
此时,齐次坐标就显示出它的魅力了,如果使用齐次坐标来表达 a' = R*a + t 的话可以写为:
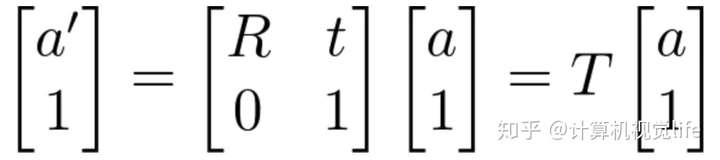
旋转和平移可以用一个矩阵T来表示,该矩阵T称为变换矩阵(transform matrix),这样欧氏变换就变成了线性关系,进行多次欧氏变换只需要连乘变换矩阵就行了,比如前面的两次欧氏变换使用齐次坐标就可以表示为:
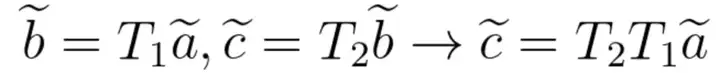
其中,波浪号代表齐次坐标。一般的,在SLAM中,b = Ta 的形式默认都是齐次坐标。
5 齐次坐标变换
平移变换
平移是指将 P 点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程。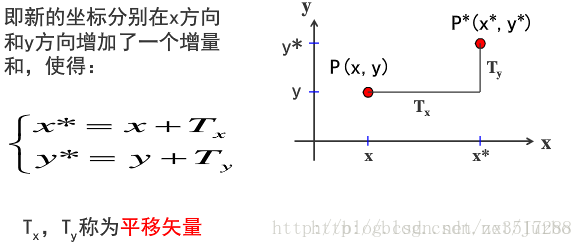
齐次坐标计算形式如下:
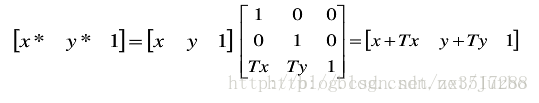
平移是一种不产生变形而移动物体的刚体变换,即物体上的每个点移动相同数量的坐标。
比例变换

齐次坐标计算形式如下:
缩放系数Sx,Sy可赋予任何正整数。值小于1,则会缩小物体的尺寸。值大于1,则会放大物体。都指定为1,物体尺寸就不会改变。
(1)Sx = Sy 比例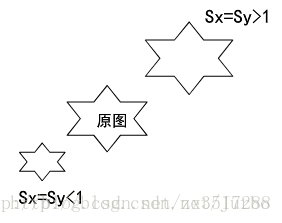
(2)Sx <> Sy 比例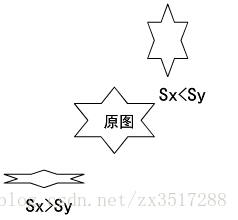
当 Sx = Sy 时,比例变换成为整体比例变换,用以下矩阵进行计算: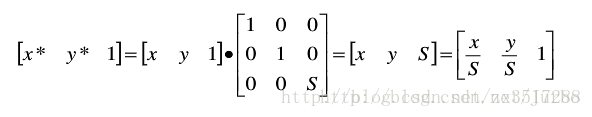
对称变换
对称变换也称为反射变化或镜像变换,变换后的图形是原图形关于某一轴线或原点的镜像。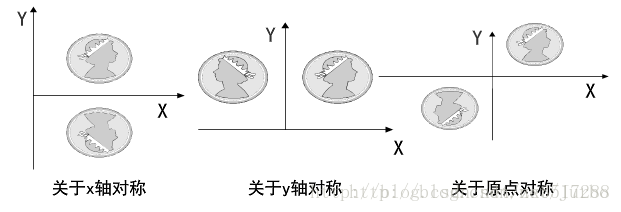
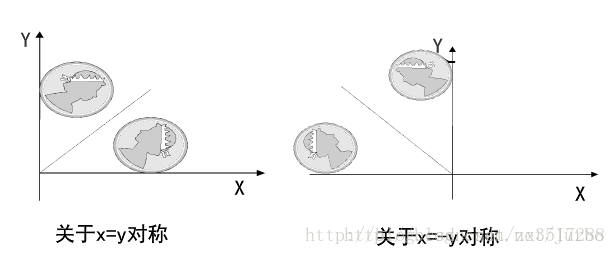
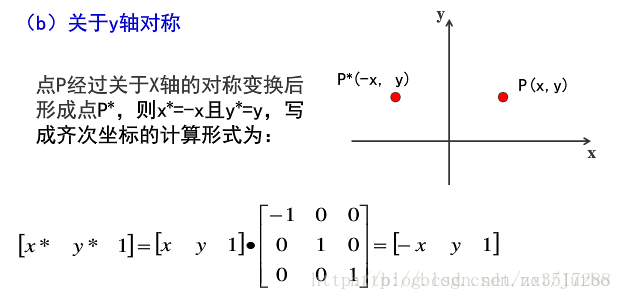
关于x轴对称
关于y轴对称
旋转变换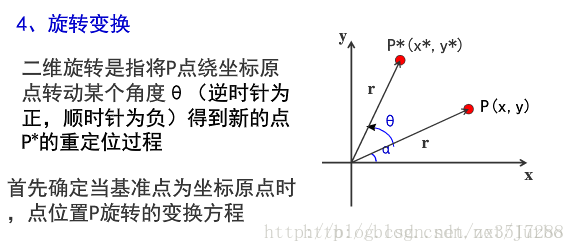
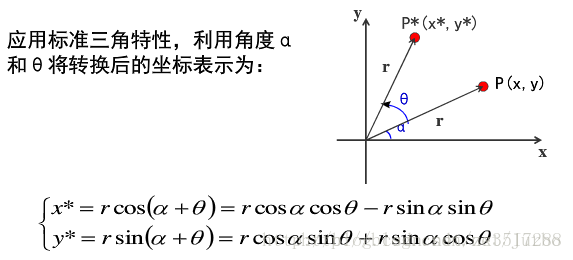


复合变换
复合变换是指图形做一次以上的几何变换,变换结果是每次的变换矩阵相乘。
从另一方面看,任何一个复杂的几何变换都可以看做是基本几何变换的组合形式。
二维复合平移变换
P 点经过两次连续平移后,其变换矩阵可以写成:
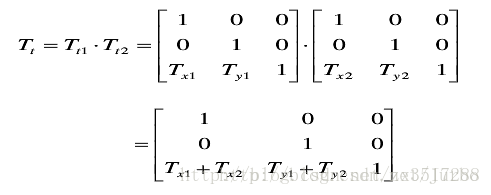
二维复合比例变换
P 点经过两个连续比例变换后,其变换矩阵可写成:

二维复合旋转变换
P 点经过两个连续旋转变换后,其变换矩阵可写成:
二维变换矩阵