Dijkstra算法

简单直观解释

详细解释(C#)

高赞详细解释(C++)   

路径规划及Python实现

路径规划及C++ 

python实现      python实现         python实现(已实现)      python实现          C++实现   C++实现   C++实现         C++实现        C实现

 

注意: Dijkstra算法 不同于 BFS的地方是，Dijkstra选择待搜索点的规则不同，它采用 最优队列 选择cost最小的待遍历节点。本质上Dijkstra算法是一个贪心算法。

　　当图形为网格图，并且每个节点之间的移动代价是相等的，那么Dijkstra算法将和BFS算法变得一样。

　　　　

　　贪心算法: 某些问题的最优解可以通过一系列的局部最优的选择即贪心选择来达到。但局部最优并不总能获得整体最优解，但通常能获得近似最优解。在每一步贪心选择中，

　　　　　　  只考虑当前对自己最有利的选择，而不去考虑在后面看来这种选择是否合理。

 

迪杰斯特拉算法 使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

Dijkstra 算法，是一个应用最为广泛的、名气也是最大的单源最短路径算法. Dijkstra 算法有一定的局限性：它所处理的图中不能有负权边

Dijkstra 算法描述：

1. 创建源顶点 v 到图中所有顶点的距离的集合 distSet，为图中的所有顶点指定一个距离值，初始均为 Infinite，源顶点距离为 0；
2. 创建 SPT（Shortest Path Tree）集合 sptSet，初始为空集合，最终要包含所有的顶点；
3. 创建一个父节点表，Ftable, 表的大小与节点数量一致；
4. 如果 sptSet 中并没有包含所有的顶点，则：
   • 选中不包含在 sptSet 中的顶点 u，u 为当前不在sptSet的最短距离顶点；
   • 将 u 包含进 sptSet，更新 Ftable里u的父节点；
   • 更新 u 的所有邻接顶点的距离值；(不必更新已在sptSet中的临节点，无有负权值，更新的是 还未加入的节点，例如: 节点1已经加入sptSet，不会再有其它路径到达1的距离更短，除非 7->1 cost = -5(负权边);另一种情况， 如果0->7=2, 7->1 = 1；则初始加入的节点是7 不是1)
   • 更新 Ftable里u 的所有邻接顶点的的父节点为u；

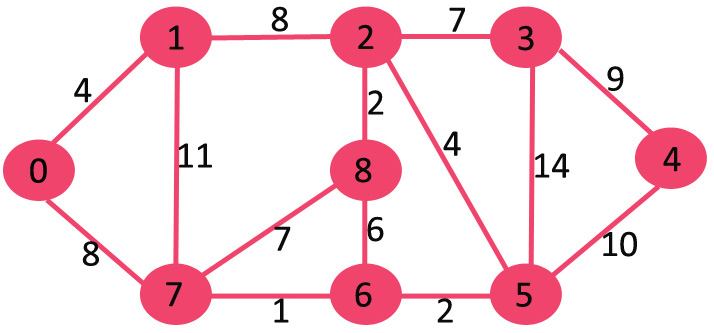
源顶点 source = 0，初始时，

• sptSet = {false, false, false, false, false, false, false, false, false};
• distSet = {0, INF, INF, INF, INF, INF, INF, INF, INF};
• Ftable = {-1,  -1,   -1,   -1,   -1,   -1,   -1,    -1,  - 1};

将 0 包含至 sptSet 中；

• sptSet = {true, false, false, false, false, false, false, false, false};

更新 0 至其邻接节点的距离；

• distSet = {0, 4, INF, INF, INF, INF, INF, 8, INF};

更新Ftable中1节点和7节点的父节点；

• Ftable = {-1,  0,   -1,   -1,   -1,   -1,   -1,    0,  - 1};

 

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 1，则将 1 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, false, false, false};

更新 1 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, INF, INF, 8, INF};

更新不在sptSet的Ftable中2节点的父节点为 1；

• Ftable = {-1,  0,   1,   -1,   -1,   -1,   -1,    0,  - 1};

 

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 7，则将 7 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, false, true, false};

更新Ftable中7节点的父节点；

• Ftable = {-1,  0,   -1,   -1,   -1,   -1,   -1,    -1,  - 1};

更新 7 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, INF, 9, 8, 15};

更新不在sptSet的Ftable中6节点和8节点的父节点为7；

• Ftable = {-1,  0,   1,   -1,   -1,   -1,   7,    0,  7};

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 6，则将 6 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, true, true, false};

更新 6 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, 11, 9, 8, 15};

更新不在sptSet的Ftable中5节点的父节点为6；

• Ftable = {-1,  0,   1,   -1,   -1,   6,   7,    0,  7};

以此类推，直到遍历结束。

• sptSet = {true, true, true, true, true, true, true, true, true};
• distSet = {0, 4, 12, 19, 21, 11, 9, 8, 14}; 最短路径距离
• Ftable = {-1,  0,   1,   2,   5,   6,   7,    0,  7};， 回溯路径