单调栈
单调栈
单调栈分为单调递增栈和单调递减栈
- 单调递增栈即栈内元素保持单调递增的栈
- 同理单调递减栈即栈内元素保持单调递减的栈
操作规则(下面都以单调递增栈为例)
- 如果新的元素比栈顶元素大,就入栈
- 如果新的元素较小,那就一直把栈内元素弹出来,直到栈顶比新元素小
加入这样一个规则之后,会有什么效果
- 栈内的元素是递增的
- 当元素出栈时,说明这个新元素是出栈元素向后找第一个比其小的元素
单调栈的代码模板
LinkedList<Integer> stack= new LinkedList<>();
arr 可以是原数组前后补最大值或者最小值,这样做的目的是解决如果遍历完数组,栈内还有元素的问题,或者栈内没有元素无法开始的问题
此模板记录的是下表,也可以直接记录数据
for(int i=0;i<arr.length;i++)
{
while (!stack.isEmpty()&&arr[stack.peek()]>arr[i])
{
stack.pop();
}
stack.push(i);
}
leetcode 84.柱状图中最大的矩形
此题目为单调递增栈,因为只有当前元素大于栈顶的元素,那么栈顶的元素高度才可以向右延伸,否则此高度延伸到此为止
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
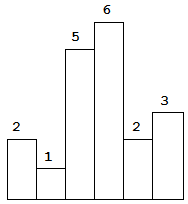
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
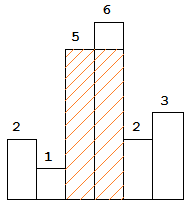
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
public int largestRectangleArea(int[] heights) {
LinkedList<Integer> stack= new LinkedList<>();
int[] new_height= new int[heights.length+2];
for(int i=1;i<new_height.length-1;i++)
{
new_height[i]=heights[i-1];
}
int left,right;
int ans=0;
for(int i=0;i<new_height.length;i++)
{
while(!stack.isEmpty()&&new_height[i]<new_height[stack.peek()])
{
int cur=stack.pop();
int l=stack.peek();
int r=i;
ans=Math.max(ans,(r-l-1)*new_height[cur]);
}
stack.push(i);
}
return ans;
}
leecode42接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
单调递减栈
public int decrea(int[] height)
{
LinkedList<Integer> stack= new LinkedList<>();
int ans=0;
for(int i=0;i<height.length;i++)
{
while (!stack.isEmpty()&&height[i]>height[stack.peek()])
{
int mid= height[stack.pop()];
if(stack.isEmpty()) break;
int right=height[i];
int h=Math.min(height[stack.peek()],right);
ans=ans+(h-mid)*(i-stack.peek()-1);
}
stack.push(i);
}
return ans;
}
leecode 85 最大矩形 hard
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
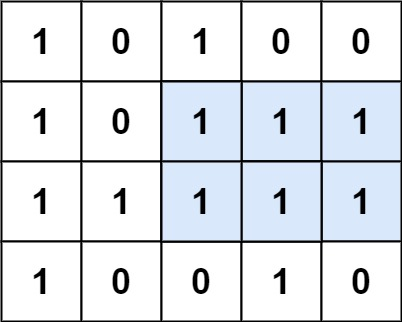
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
示例 3:
输入:matrix = [["0"]]
输出:0
示例 4:
输入:matrix = [["1"]]
输出:1
示例 5:
输入:matrix = [["0","0"]]
输出:0
提示:
rows == matrix.length
cols == matrix[0].length
0 <= row, cols <= 200
matrix[i][j] 为 '0' 或 '1'
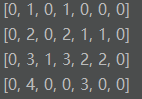
这道题与上面求柱状图中最大矩形面积有异曲同工之妙,将每一行往上看做一个柱状图不就转化为上面的题吗,如何转化,就是构造一个新的矩阵,这个矩阵盛放当前行,当前列连续的格子的数量,注意连续
对于上图中的示例构造如下矩阵
public int compute(int[][] arr,int row)
{
int ans=0;
LinkedList<Integer> stack= new LinkedList<>();
//每一行单调递增栈
int l,r;
for(int i=0;i<arr[0].length;i++)
{
while (!stack.isEmpty()&&arr[row][i]<arr[row][stack.peek()])
{
int curr=stack.pop();
l=stack.peek();
r=i;
ans= Math.max(ans,(r-l-1)*arr[row][curr]);
}
stack.push(i);
}
return ans;
}
public int maximalRectangle(char[][] matrix) {
if(matrix.length==0) return 0;
int[][] height_matrix = new int[matrix.length][matrix[0].length+2];
//构造高度矩阵
for(int i=1;i<height_matrix[0].length-1;i++)
{
height_matrix[0][i]=matrix[0][i-1]-'0';
}
for(int i=1;i<height_matrix.length;i++)
{
for(int j=1;j<height_matrix[0].length-1;j++)
{
if(matrix[i][j-1]=='0')continue;
height_matrix[i][j]=height_matrix[i-1][j]+1;
}
}
int max= 0;
for(int i=0;i<height_matrix.length;i++)
{
max=Math.max(compute(height_matrix,i),max);
int a=5;
}
return max;
}
参考
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/84-by-ikaruga/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号