C++ 函数部分(2)
C++函数的递归调用
函数可以直接或间接地调用自身,称为递归调用。所谓直接调用自身,就是指在一个函数的函数体中出现了对自身的调用表达式,例如:
void fun1(void)
{
//do something
fun1(); //调用fun1自身
//do something
}
函数间接调用自身,就是通过调用其它函数的同时在其它函数中有调用了自己,例如:
void fun1(void)
{
//do something
fun2(); //调用fun1自身
//do something
}
void fun2(void)
{
//do something
fun1();
//do something
}
这里fun1调用了fun2,而fun2又调用了fun1, 于是就构成了递归。
递归算法的实质是将原有的问题分解为新的问题,而解决新问题时又用到了原有问题的解法。按照这一原则分解下去,每次出现的新问题都是原有问题的简化的子集,而最终分解出来的问题,是一个已知解的问题。
递归的过程有两个阶段:
第一个阶段:递推。 讲原问题不断分解为新的子问题,逐渐从未知向已知推进,最终达到已知的条件,即递归结束的条件,这时递推阶段结束。例如,求5!,可以这样分解:
5!= 5*4!->4!=4*3!->3! =3*2! –> 2!=2*1!->1! = 1*0!->0! =1
未知--------------------------------------------------------------------->已知
第二阶段:回归。从已知条件出发,按照递推的逆过程,逐一求值回归,最后达到递推的开始处,结束回归阶段,完成递归调用。例如,求5!的回归阶段如下:
5!= 5*4!<- 4!=4*3!<- 3! =3*2! <– 2!=2*1! <- 1! = 1*0! <- 0! =1
未知<--------------------------------------------------------------------- 已知
1.求n!的值
分析:计算n!的公式如下:
这是一个递归形式的公式,在描述"阶乘"算法时又用到了"阶乘"。递归的结束条件是 n = 0.
#include <iostream>
using namespace std;
long fac(int n)
{
long f;
if(n<0) cout<<"n<0,data error!"<<endl;
else if(n == 0) f = 1;
else f = fac(n-1)*n;
return (f);
}
void main()
{
long fac(int n); //函数声明
int n;
long y;
cout<<"Enter a positive integer: ";
cin>>n;
y = fac(n);
cout<<n<<"! = "<<y<<endl;
fflush(stdin);
getchar();
}
2.用递归法计算从n个人中选择k个人组成一个委员会的不同组合数。
分析:由n个人里选k个人的组合数 = 由(n-1)个人里选k个人的组合数 + 由(n-1)个人里选(k-1)个人的组合数。递推的结束条件是n == k || k == 0 , 这时的组合数为1。
#include <iostream>
using namespace std;
void main()
{
int n, k;
int comm(int n , int k);
cout<<"Enter n and k :";
cin>>n>>k;
cout<<comm(n,k)<<endl;
fflush(stdin);
getchar();
}
int comm(int n, int k)
{
if(k>n) return 0;
else if(n == k || k == 0) return 1;
else
return comm(n-1,k)+comm(n-1,k-1);
}
结果:
input 18 5 output : 8568
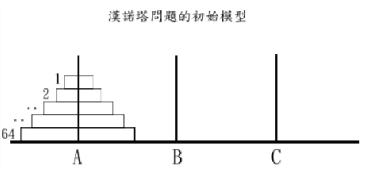
3. 汉诺塔问题
有三根针A、B、C。A针上有n个盘子,盘子大小不等,大的在下,小的在上,如下图所示。要求把这n个盘子从A针移动到C针,在移动过程中可以借助B针,每次只充许移动一个盘子,且在移动过程中在三根针上都保持大盘在下,小盘在上。
分析:
将n个盘子从A针移动到C针可以分解为下面3个步骤:
1.将A上n-1个盘子移动到B针上(借助C针);
2.把A针上剩下的一个盘子移动到C针上;
3.将n-1个盘子从B针移动到C针上(借助A针)
事实上,上面3个步骤包含两种操作:
1.将多个盘子从一个针移动到另一个针上,这是一个递归的过程。
2.将1个盘子从一个针上移动到另一个针上。
那么就可以用两个函数分别实现上面的两种操作,用hanoi函数实现第一种操作,用move函数实现第二种操作。
#include <iostream>
#include <iomanip>
using namespace std;
void move(char getone, char putone)
{
static int i = 1;
cout<<"Step."<<setw(2)<<i<<" : "<<getone<<"-->"<<putone<<endl;
i++;
}
void hanoi(int n, char one, char two,char three)
{
void move(char getone , char putone);
if(n == 1) move(one , three);
else
{
hanoi(n-1,one,three,two);
move(one,three);
hanoi(n-1,two,one, three);
}
}
void main()
{
void hanoi(int n , char one , char two, char three);
int m;
cout<<"Enter the number of diskes : " ;
cin>>m;
cout<<"the steps to moving "<<m<<" diskes:"<<endl;
hanoi(m,'A','B','C');
fflush(stdin);
getchar();
}
运行结果:
Enter the number of diskes : 3
the steps to moving 3 diskes:
Step. 1 : A-->C
Step. 2 : A-->B
Step. 3 : C-->B
Step. 4 : A-->C
Step. 5 : B-->A
Step. 6 : B-->C
Step. 7 : A-->C
函数的参数传递
在函数为被调用时,函数的形参并不占有实际的内存空间,也没有实际的值。只有在函数被调用时才为形参分配存储单元,并将实参与形参结合。结合过程叫做参数传递,有值传递和引用传递两种方式。
1.值传递
值传递是指当发生函数调用时,给形参分配内存空间,并用实参来初始化形参(直接将实参的值传递给形参)。这一过程是参数值的单向传递过程,一旦形参获得了值便与实参脱离关系,此后无论形参发生了怎样的改变,都不会影响到实参。
#include <iostream>
using namespace std;
void swap(int a ,int b);
void main()
{
int x(5),y(10);
cout<<"x = "<<x<<" y = "<<y<<endl;
swap(x,y);
cout<<"x = "<<x<<" y = "<<y<<endl;
fflush(stdin);
getchar();
}
void swap(int a, int b)
{
int t;
t = a;
a = b;
b = t;
}
上例中,swap之前x,y分别初始化为5和10,调用swap时, 实参x,y把值传递给形参a,b 由于这里是值传递,是单向的,所以实参x,y把值5,10传递给a,b之后就跟a,b没有关系了, 在swap里面a,b借助临时变量t交换了值,但是这是a,b之间交换了值不影响x,y的值。
2.引用传递
引用是一种特殊类型的变量,可以被认为是另一个变量的别名。通过引用名与通过被引用的变量名访问变量的效果是一样的,例如:
int i,j;
int &r = i; // 建立一个int型的引用r, 并将其初始化为变量i的一个别名
j = 10;
r = j; //相当于i = j;
使用引用时需要注意两个问题:
1.声明一个引用时,必须同时对它进行初始化,使它指向一个已存在的对象。
2.一旦一个引用被初始化后,就不能改为指向其它对象。也就是说,一个引用,从它诞生之时起,就必须确定是哪个变量的别名,而且始终只能作为这个变量的别名,不能另作它用。
&放在变量前面就是引用符号
#include <iostream>
using namespace std;
void swap(int& a, int& b);
void main()
{
int x(5), y(10);
cout<<"x = "<<x<<" y = "<<y<<endl;
swap(x,y);
cout<<"x = "<<x<<" y = "<<y<<endl;
fflush(stdin);
getchar();
}
void swap(int&a , int& b)
{
int t;
t = a;
a = b;
b = t;
}
上面的例子就是引用传递可以实现x,y的值交换操作。
引用传递与值传递的区别只是函数的形参写法不同,主调函数中的调用表达式完全一样。
内联函数
函数调用时,需要保存现场和返回地址,然后转到子函数的代码起始地址去执行。子函数执行完后,又要取出先前保存的返回地址和现场状态,再继续执行。这一切都需要时间和空间方面的开销,所以频繁调用函数会降低程序的执行效率。对于一些功能简单、规模较小又使用频繁的函数,可以设计为内联函数。内联函数不是在调用时发生控制转移,而是在编译时将函数体嵌入在每个调用处。这样就节省了参数传递、控制转移等开销。
内联函数在定义时使用关键字inline, 语法形式如下:
inline 类型说明符 被调函数名(含类型说明的形参表){函数体语句;}
使用内联函数时应注意:
1.内联函数体内一般不能有循环语句和switch语句;
2.内联函数的定义必须出现在第一次被调用之前;
3.对内联函数不能进行异常接口声明
通常内联函数应该是比较简单的函数,结构简单、语句少。如果将一个复杂的函数定义为内联函数,反而会造成代码膨胀,增大开销。这种情况下,多数编译器都会自动将其转换为普通函数来处理。
因此,inline关键字只是表示一个要求,编译器并不承诺将inline修饰的函数作为内联。而没有用inline修饰的函数也可能编译为内联函数。
C++中充许给函数设置默认的形参值
函数在定义时可以预先声明默认的形参值。调用时如果给出实参,则用实参初始化形参;如果没有给出实参,则采用预先声明的默认形参值。例如:
int add(int x = 5, int y = 6) // 声明默认形参值
{
return x + y;
}
void main(void)
{
add(10,20); //用实参来初始化形参,实现10+20
add(10); //形参x采用实参值10,y采用默认值6, 实现10+6
add(); //x和y都采用默认值,分别为5和6,实现5+6
}
add();
retrun (x + y);
注意:在相同的作用域内,默认形参值的说明应保持唯一,但如果在不同的作用域内,充许说明不同的默认形参,例如:
int add(int x = 1, int y = 2);
void main(void)
{
int add(int x = 3, int y = 5);
add(); //使用局部默认形参值(实现3+5)
}
void fun(void)
{
//do something
add(); //使用全局默认形参值(实现1+2)
}
C++的函数重载,就是通过调用相同的函数名来响应不同的操作。在两个以上的函数中,具有相同的函数名,但是形参的个数或类型不同,编译器根据实参和形参的类型及个数的最佳匹配,自动确定调用哪个函数,这就是函数的重载。
1.判断一个数是否为质数(质数又称为素数)
质数又称之为素数。指在一个大于1的自然数中,除了1和此整数自身外,没法被其它自然数整除的数。即只有两个正因数(1和自己)的自然数即为素数。比1大但不是素数的数称为合数。1和0既非素数也非合数。合数是由若干个质数相乘而得到的。
取模运算:a % p(或a mod p),表示a除以p的余数。
注意:n % p 得到结果的正负由被除数n决定,与p无关。例如:7%4 = 3, -7%4 = -3, 7%-4 = 3, -7%-4 = -3。
#include <iostream>
#include <math.h>
using namespace std;
int prime(int n);
int main()
{
int n;
cout<<"Enter an integer:";
cin>>n;
if(prime(n))
cout<<n<<"是素数"<<endl;
else
cout<<n<<"不是素数"<<endl;
fflush(stdin);
getchar();
}
int prime(int n)
{
int j,flag;
flag = 1;
for(j = 2; j<=sqrt(double(n));j++)
{
if(n % j == 0)
{
flag = 0;
break;
}
}
if(flag)
return 1;
else return 0;
}
2.求两个整数的最大公约数和最小公倍数。
最大公约数,也称为最大公因数,最大公因子,指两个或多个整数共有约数中最大的一个。a,b的最大公约数记为(a,b),同样的,a,b,c的最大公约数记为(a,b,c),多个整数的最大公约数也有同样的记号。记号(a)表示a的约束中最大的那个数。与最大公约数相对应的概念是最小公倍数,a,b的最小公倍数记为[a,b]。
如果数a能被数b整除,a就叫做b的倍数,b就叫做a的约数。约数和倍数都表示一个数与另一个数的关系,不能单独存在。
几个自然数,公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。例如:12,16的公约数有1,2,4,其中最大的一个是4,4是12与16的最大公约数,一般记为(12,16) = 4.
几个自然数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。例如:4的倍数有4,8,12,……,6的倍数有6,12,……,4和6的公倍数有12,24,……,其中最小的是12,所以[4,6] = 12.两数互质最小公倍数为两数乘积。
互质又叫互素。若N个整数的最大公因数是1,则称这N个整数互质。例如8,10的最大公因数是2,不是1,因此不是整数互质。7,10,13的最大公因数是1,因此这是整数互质。下面分析两种求最大公约数的方法:
(1)求差判定法.
如果两个数相差不大,可以用大数减去小数,所得的差与小数的最大公约数就是原来两个数的最大公约数.例如:求78和60的最大公约数.78-60=18,18和60的最大公约数是6,所以78和60的最大公约数是6.
如果两个数相差较大,可以用大数减去小数的若干倍,一直减到差比小数小为止,差和小数的最大公约数就是原来两数的最大公约数.例如:求92和16的最大公约数.92-16=76,76-16=60,60-16=44,44-16=28,28-16=12,12和16的最大公约数是4,所以92和16的最大公约数就是4.
(2)辗转相除法.
当两个数都较大时,采用辗转相除法比较方便.其方法是:
以小数除大数,如果能整除,那么小数就是所求的最大公约数.否则就用余数来除刚才的除数;再用这新除法的余数去除刚才的余数.依此类推,直到一个除法能够整除,这时作为除数的数就是所求的最大公约数.
例如:求4453和5767的最大公约数时,可作如下除法.
5767÷4453=1余1314
4453÷1314=3余511
1314÷511=2余292
511÷292=1余219
292÷219=1余73
219÷73=3
于是得知,5767和4453的最大公约数是73.
辗转相除法适用比较广,比短除法要好得多,它能保证求出任意两个数的最大公约数.
而最小公倍数可以借助最大公约数来求,分两步:
1.利用辗除法或其它方法求得最大公约数
2.最小公倍数等于两数之积除以最大公约数
举例:12和8的最大公约数为4,12*8/4 = 24 那么12和8的最小公倍数为24.
C++递归版:
#include<iostream>
using namespace std;
int func(int a, int b)
{
int min, max;
max = a>b?a:b;
min = a<b?a:b;
if(max%min ==0)
return min;
else
return func(min,max%min);
}
int main()
{
int a, b;
cout<<"输入两个整数,用空格分隔,按回车结束:";
cin>>a>>b;
cout<<"这两个整数的最大公约数是:"<<func(a,b)<<endl;
cout<<"这两个整数的最小公倍数是:"<<((a*b)/func(a,b))<<endl;
fflush(stdin);
getchar();
}
非递归版:
#include<iostream>
using namespace std;
int func(int a, int b)
{
int min, max,r;
max = a>b?a:b;
min = a<b?a:b;
if(max%min ==0)
return min;
while(max%min != 0)
{
r=max%min;
max = min;
min =r;
}
return min;
}
int main()
{
int a, b;
cout<<"输入两个整数,用空格分隔,按回车结束:";
cin>>a>>b;
cout<<"这两个整数的最大公约数是:"<<func(a,b)<<endl;
cout<<"这两个整数的最小公倍数是:"<<((a*b)/func(a,b))<<endl;
fflush(stdin);
getchar();
}
运行结果:
输入两个整数,用空格分隔,按回车结束:12 8
这两个整数的最大公约数是:4
这两个整数的最小公倍数是:24
3.编写递归函数GetPower(int x, int y ) 计算x的y次幂,在主程序中实现输入输出。
int func(int x , int y)
{ static int sum = 1;
if(y ==1) sum *=x;
else sum *=func(x,y-1);
return sum;
}
这样写是不行的,如输入5,3 则输出结果为625,为什么呢?
因为sum = sum*sum*func(5,1);这里func(5,1)返回的sum会改变前面的sum值,此外这里的运算是自右向左运算的,也就是说返回的sum = 5 ,然后最右边两个sum 运算之后sum值25,然后再于剩下的sum运算,此时是25*25 所以输入5,3之后输出的结果是625.
C++版:
#include <iostream>
using namespace std;
int GetPower(int x, int y)
{
if(x == 0) return 0;
if(y == 0) return 1;
if(y == 1) return x;
if(x>1&&y>1) return (GetPower(x,y-1)*x);
}
int main()
{
int a, b;
cout<<"Input a and b:";
cin>>a>>b;
cout<<"The result is: "<<GetPower(a,b)<<endl;
fflush(stdin);
getchar();
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号