哈夫曼树
哈夫曼树的相关定义
- 从树上一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目(边的数量)称为路径长度
- 树中的结点常常被赋予一个表示某种意义的数值，称为该节点的权
- 从树的根到一个结点的路径长度与该节点上权值的乘积被称为该节点的带权路径长度
- 树中所有的叶节点的带权路径长度之和被称为该树的带权路径长度，记为
\[ WPL = \sum_{i=1}^{n}w_{i}l_{i}
\]
在含有n个带权叶节点的二叉树中，带权路径长度WPL最小的二叉树被称为哈夫曼树，也称为最有二叉树
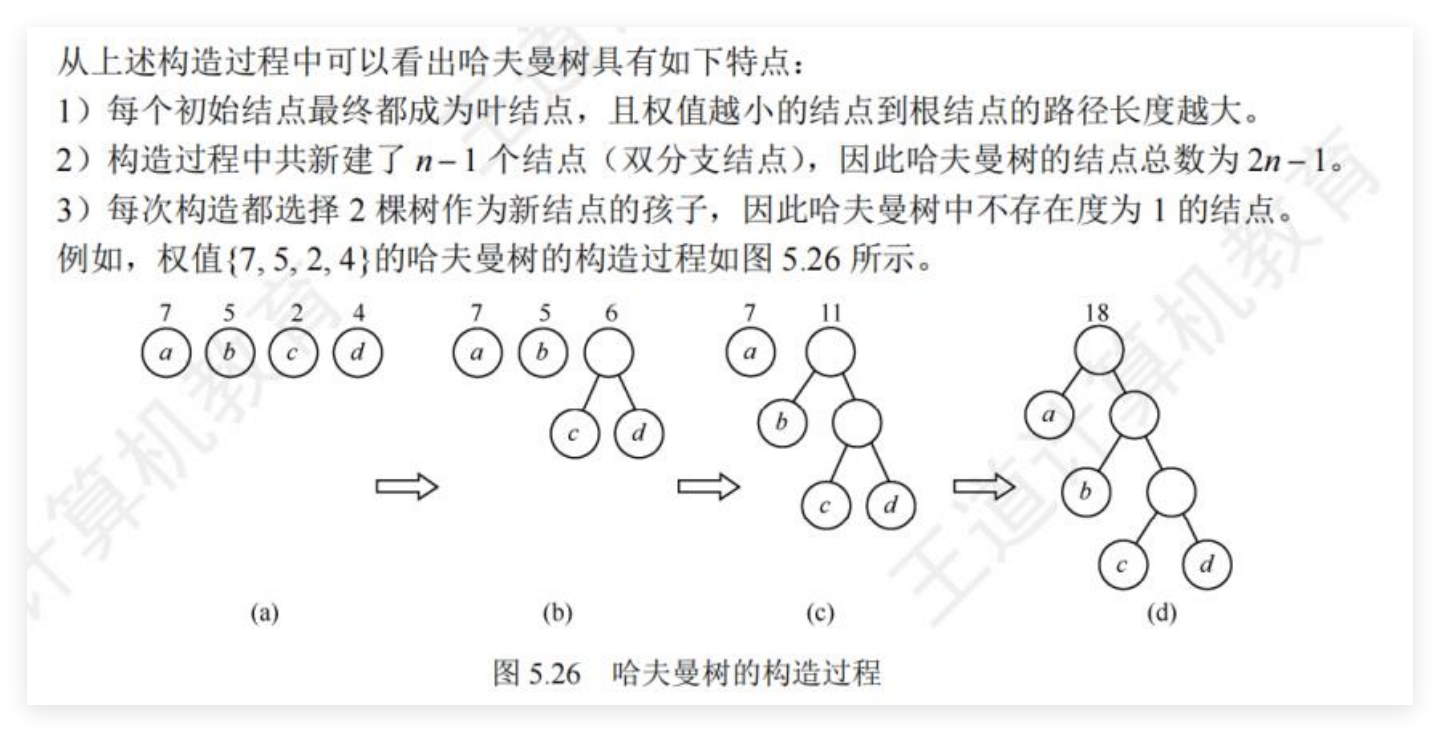
哈夫曼树的构造
哈夫曼树的性质
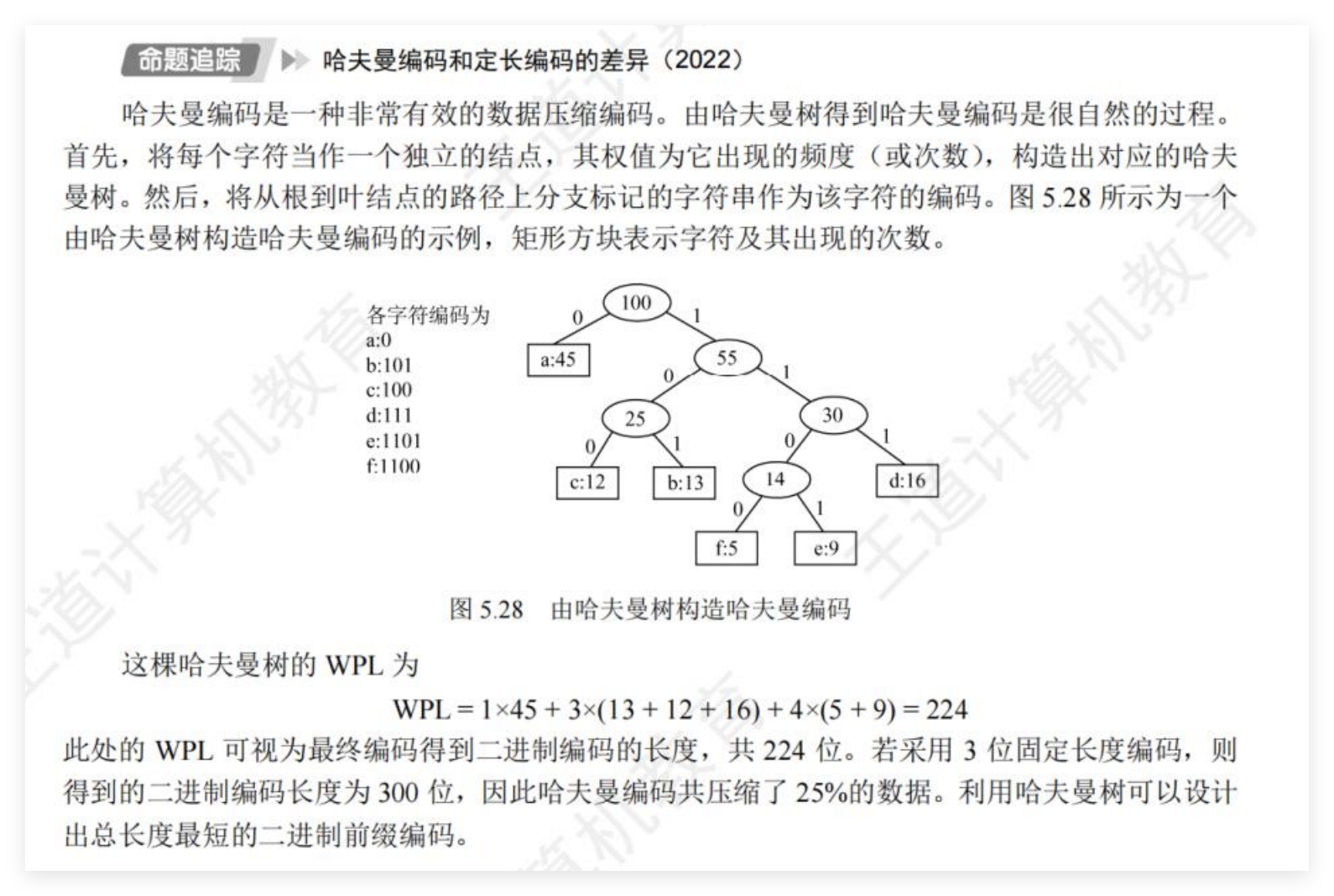
哈夫曼编码
具有n个不同权值的叶节点的哈夫曼树的形状一定是唯一的；这句话是错的，因为我们任意交换左右子树，得到的新树也是哈夫曼树
例题
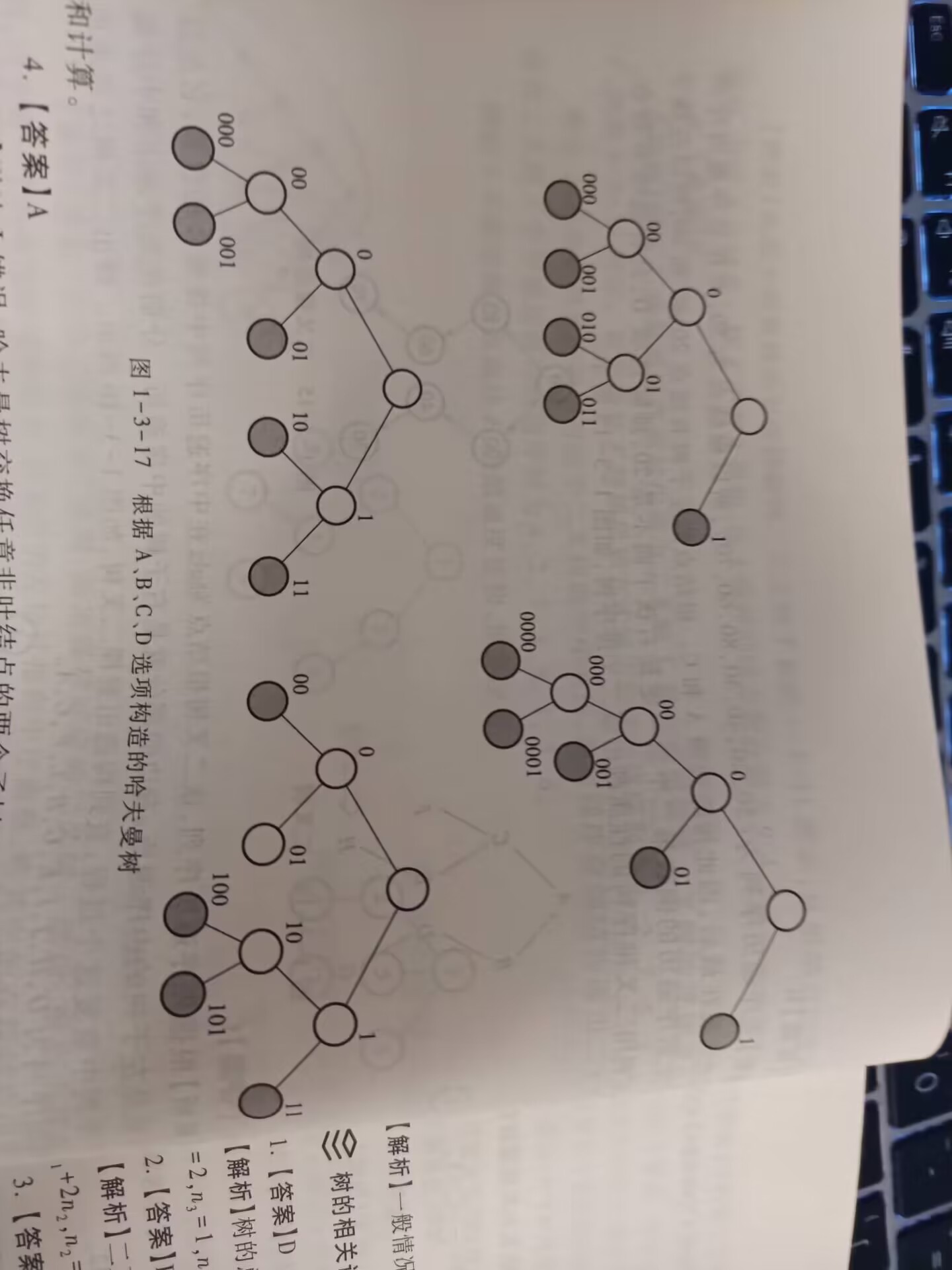
下列编码方案不属于哈夫曼编码的是:()
A 000,001,010,011,1
B 0000,0001,001,01,1
C 000,001,01,10,11
D 00,100,101,11
解析：四个选项都满足的前缀码的定义，但是哈夫曼编码的每个元素都可以等价为哈夫曼树中的叶节点，如果我们画出哈夫曼树的话，会发现01这个叶子结点没有被编码
