原码的除法运算
原码的除法有两种方法,它们分别是恢复余数法和不恢复余数法
恢复余数法
在原码除法中,参加运算的被除数和除数均采用原码表示,所得的商和余数也采用原码表示。运算时,符号位单独处理,被除数和除数的绝对值相除。为了保证定点除法的运算结果不超过机器所能表示的定点数据范围,在进行除法之前必须判定被除数和除数是否满足定点小数除法或定点整数除法的要求,如果不满足要求,由于运算结果会将产生溢出,因此不能继续进行除法运算。下面以定点小数除法为例,讨论原码恢复余数法的算法。
定点小数的原码恢复余数法由以下步骤实现:
- 判溢出,要求|被除数|<|除数|。若|被除数|>|除数|,则除法将发生溢出。
- 符号位单独处理,商的符号由被除数和除数符号的异或运算求得。
- 用被除数和除数的数值部分进行运算,被除数减去除数。
- 若所得余数为正,表示够减,相应位上商为1,余数左移一位(相当于除数右移)减去除数;若所得余数为负,表示不够减,相应位上商为0,余数加上除数(即恢复余数),再左移一位后减去除数。
- 重复第(4)步,直到求得所要求的商的各个位为止


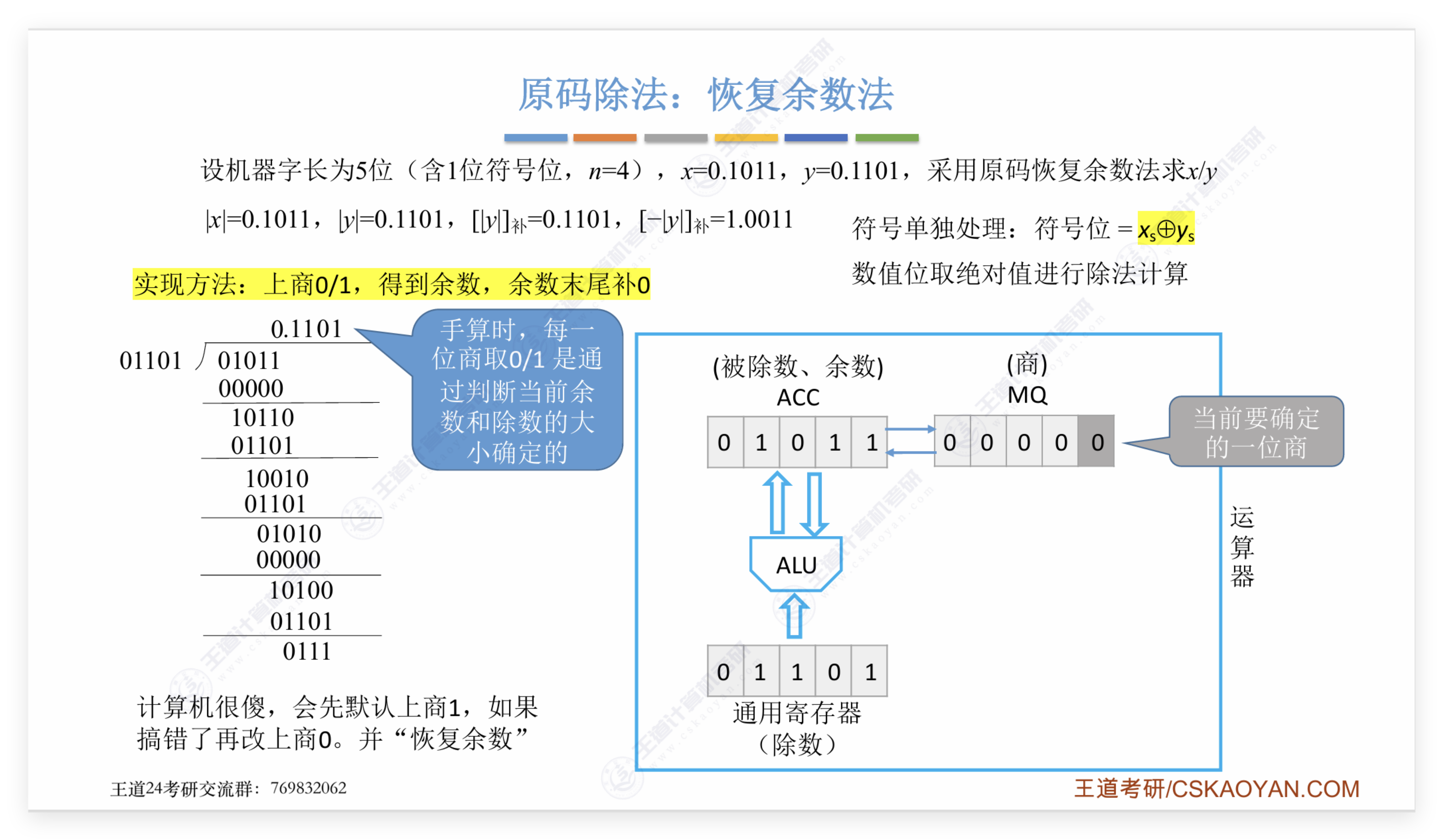
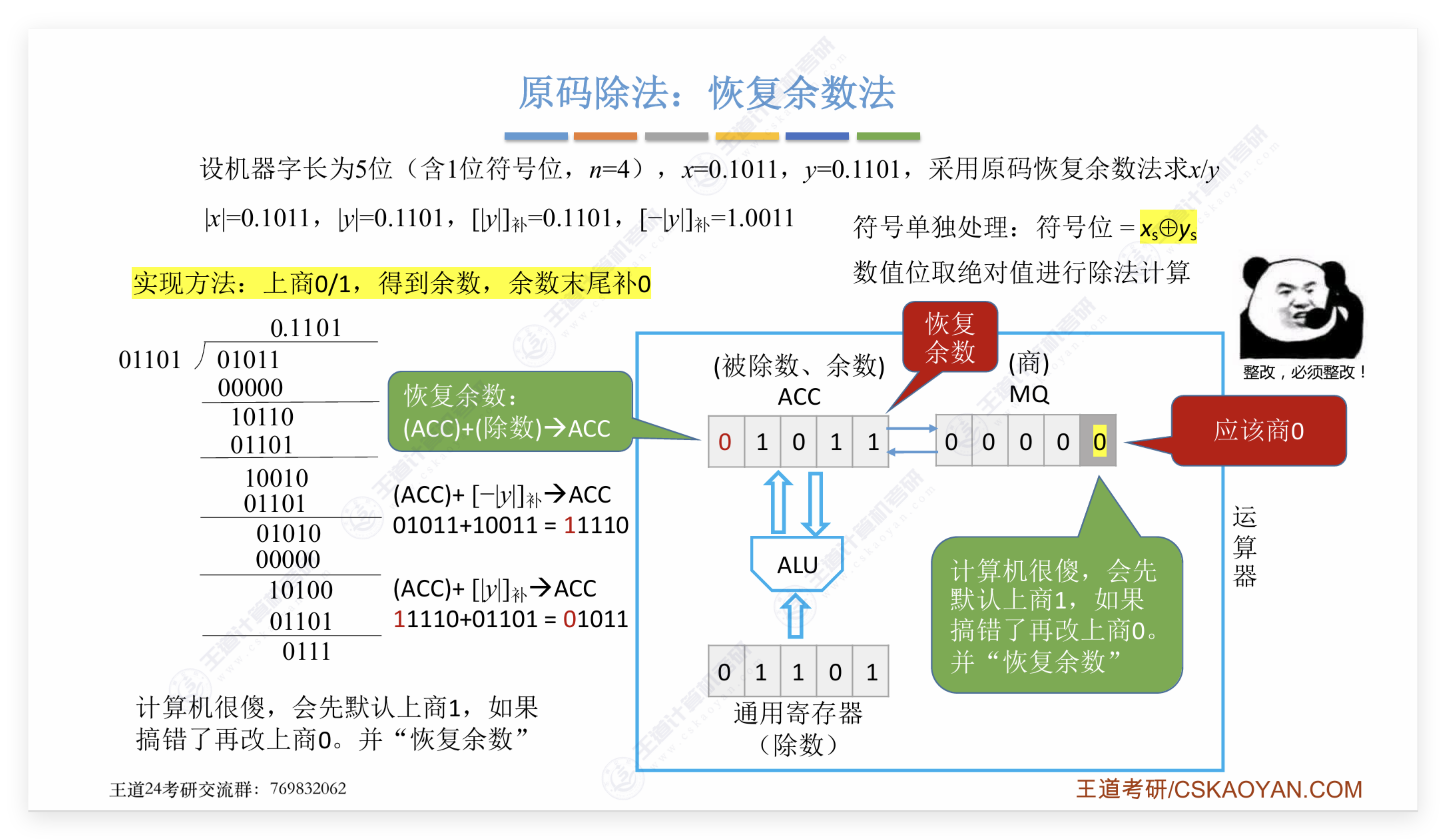
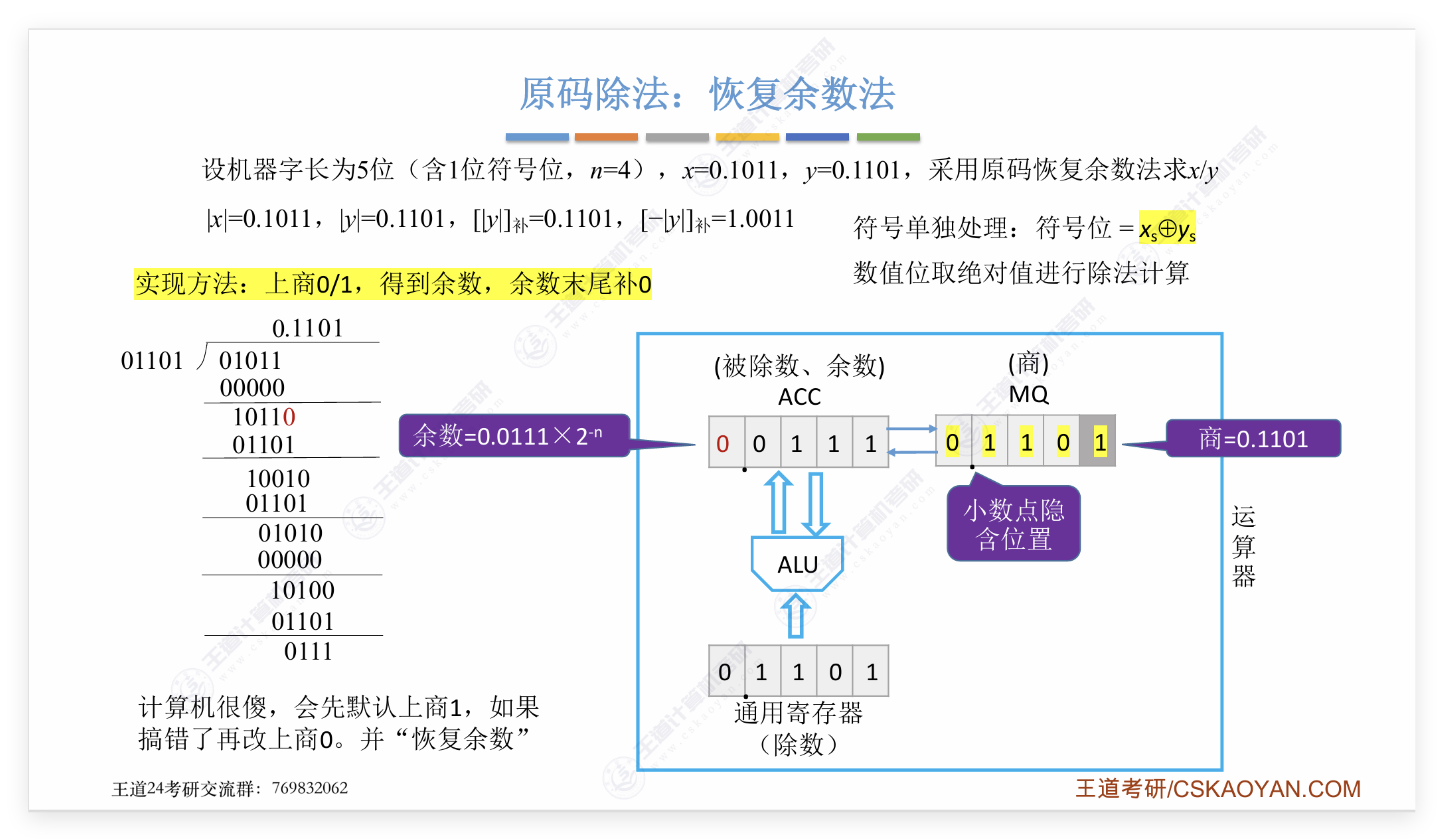
这里需要注意的一点是,王道和袁春风版的教材使用的均是单符号位,为什么不担心侵占问题呢?这是因为我们可以证明,在除法不发生溢出的情况下双符号位的结果一定会是"00"或者"11",不可能出现"10"和"01",所以单符号位也可以反映结果的正负
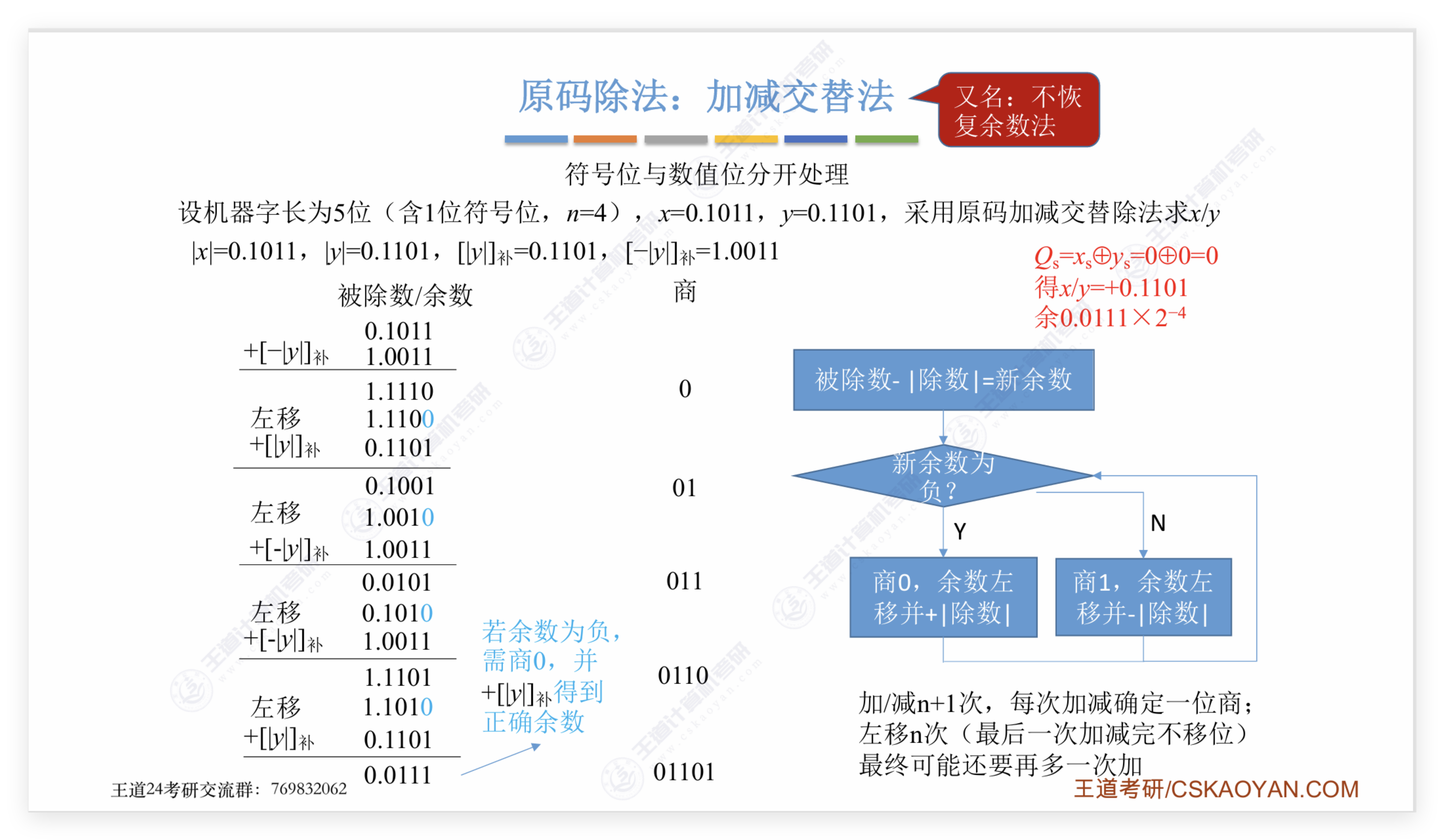
不恢复余数法(加减交替法)
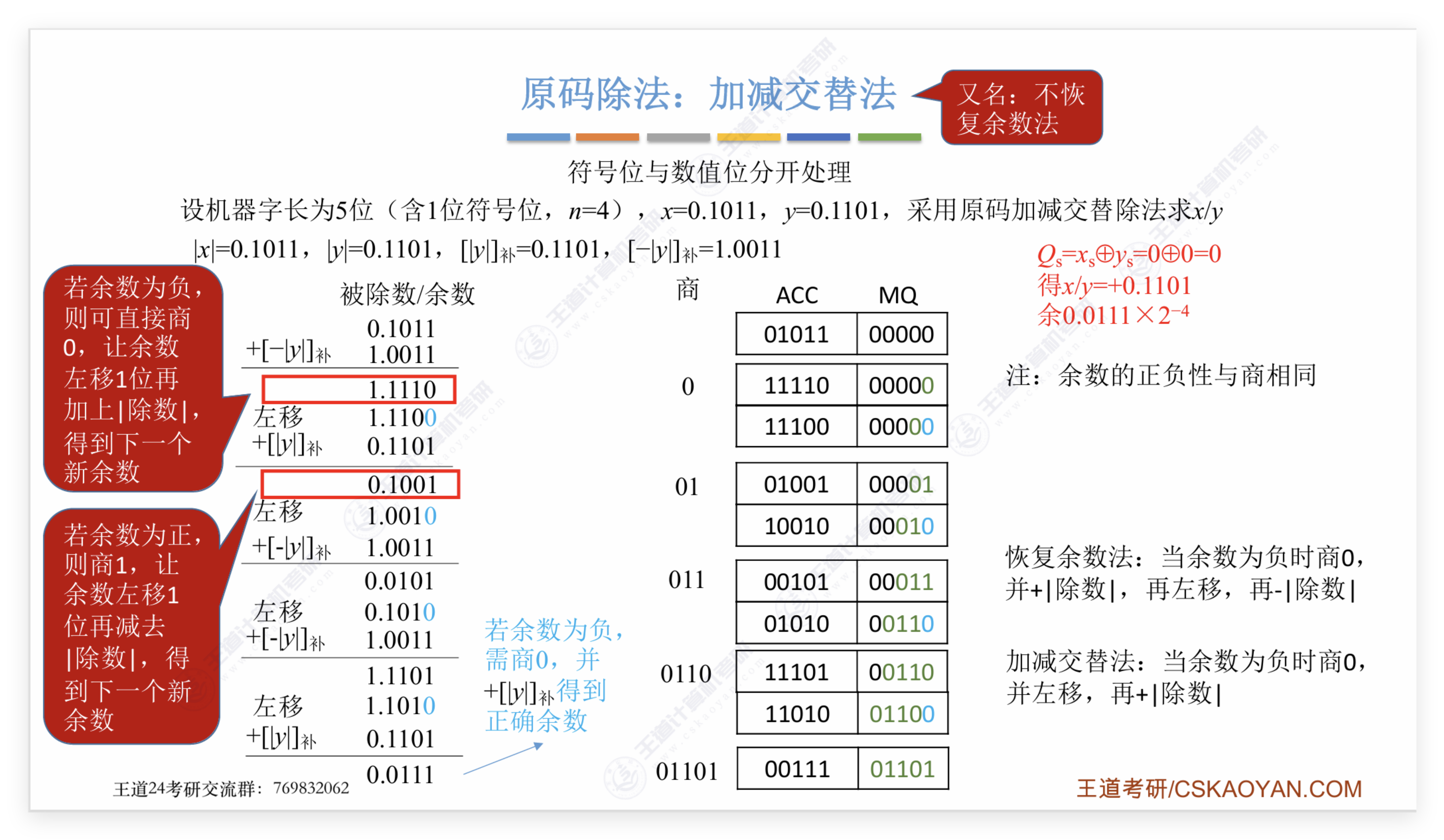


 浙公网安备 33010602011771号
浙公网安备 33010602011771号