【今日爽文】重学wqs二分之我是方案构造者
引入：最小度限制生成树
将连接 \(s\) 的边称为 白边。我们人为地控制“最小”生成树的白边数量，那么其权值一定先减小后增大。其中顶点为真正最小生成树的白边数量。
发现其有凹凸性，于是考虑 wqs 二分，具体如何操作不再详细说明，最终复杂度是 \(O(n\log n+n\log W)\)。
除此之外，题目还让我们判断无解。怎么判断呢？我们都知道最后二分出来的点不一定就是 \(t\)，而是长这样（不用在意为什么它是凸的）：
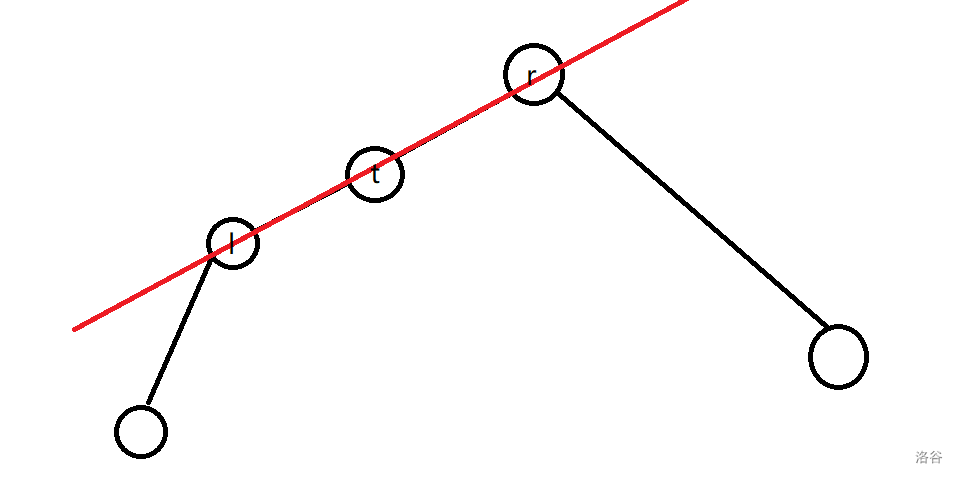
所以我们找到这里的 \(l\) 和 \(r\)，看看是否有 \(l\leq t\leq r\) 就行啦。
接下来看下一道题：MST Company
它要求我们在上一道题的基础上输出方案。
“直接像上题一样解出答案，然后算一遍不就可以了吗？”
我该怎么保证一定有 \(t\) 条白边而不是 \(l\) 或者 \(r\) 条？
“......”
接下来介绍一种方法：
先贴着 下界（\(l\)）做一次，算出哪些白边是一定要的（必要白边）。然后贴着 上界（\(r\)）做一次，算出最多有多少条白边。
定义 \(f_i\) 为保证最小生成树的情况下，最多有多少条权值 \(>i\) 的白边能在生成树中。\(f_i\) 可以在贴上界的时候算出。
然后重新贴 下界（\(l\)）做一次，按边权从小到大加入。假设现在边权为 \(i\)，白边数量为 \(now\)，并且已经算了边权为 \(i\) 的必要白边。那么只要 \(now+f_i<t\)，我就加一条边权为 \(i\) 的非必要白边，知道无边可加或者 \(now+f_i=t\)。
容易知道，这样构造一定能构造出一种白边数量为 \(t\) 的最小生成树。
注意前面要像上道题一样判无解。
欢迎纠错与指正，但我并不保证我能完全理解以及回答你们的问题。
